Clustering and Search in Multi-Dimensional Spaces¶
cv::kmeans¶
- double kmeans(const Mat& samples, int clusterCount, Mat& labels, TermCriteria termcrit, int attempts, int flags, Mat* centers)¶
Finds the centers of clusters and groups the input samples around the clusters.
Parameters: - samples – Floating-point matrix of input samples, one row per sample
- clusterCount – The number of clusters to split the set by
- labels – The input/output integer array that will store the cluster indices for every sample
- termcrit – Specifies maximum number of iterations and/or accuracy (distance the centers can move by between subsequent iterations)
- attempts – How many times the algorithm is executed using different initial labelings. The algorithm returns the labels that yield the best compactness (see the last function parameter)
- flags –
It can take the following values:
- KMEANS_RANDOM_CENTERS Random initial centers are selected in each attempt
- KMEANS_PP_CENTERS Use kmeans++ center initialization by Arthur and Vassilvitskii
- KMEANS_USE_INITIAL_LABELS During the first (and possibly the only) attempt, the
- function uses the user-supplied labels instaed of computing them from the initial centers. For the second and further attempts, the function will use the random or semi-random centers (use one of KMEANS_*_CENTERS flag to specify the exact method)
- centers – The output matrix of the cluster centers, one row per each cluster center
The function
kmeans
implements a k-means algorithm that finds the
centers of
clusterCount
clusters and groups the input samples
around the clusters. On output,
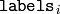 contains a 0-based cluster index for
the sample stored in the
contains a 0-based cluster index for
the sample stored in the
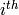 row of the
samples
matrix.
row of the
samples
matrix.
The function returns the compactness measure, which is computed as
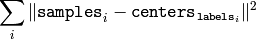
after every attempt; the best (minimum) value is chosen and the corresponding labels and the compactness value are returned by the function. Basically, the user can use only the core of the function, set the number of attempts to 1, initialize labels each time using some custom algorithm and pass them with ( flags = KMEANS_USE_INITIAL_LABELS ) flag, and then choose the best (most-compact) clustering.
cv::partition¶
- template<typename _Tp, class _EqPredicate> int()¶
- partition(const vector<_Tp>& vec, vector<int>& labels, _EqPredicate predicate=_EqPredicate())¶
Splits an element set into equivalency classes.
Parameters: - vec – The set of elements stored as a vector
- labels – The output vector of labels; will contain as many elements as vec . Each label labels[i] is 0-based cluster index of vec[i]
- predicate – The equivalence predicate (i.e. pointer to a boolean function of two arguments or an instance of the class that has the method bool operator()(const _Tp& a, const _Tp& b) . The predicate returns true when the elements are certainly if the same class, and false if they may or may not be in the same class
The generic function
partition
implements an
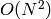 algorithm for
splitting a set of
algorithm for
splitting a set of
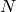 elements into one or more equivalency classes, as described in
http://en.wikipedia.org/wiki/Disjoint-set_data_structure
. The function
returns the number of equivalency classes.
elements into one or more equivalency classes, as described in
http://en.wikipedia.org/wiki/Disjoint-set_data_structure
. The function
returns the number of equivalency classes.
Fast Approximate Nearest Neighbor Search¶
This section documents OpenCV’s interface to the FLANN library. FLANN (Fast Library for Approximate Nearest Neighbors) is a library that contains a collection of algorithms optimized for fast nearest neighbor search in large datasets and for high dimensional features. More information about FLANN can be found in [muja_flann_2009] .
flann::Index¶
- flann::Index¶
The FLANN nearest neighbor index class.
namespace flann
{
class Index
{
public:
Index(const Mat& features, const IndexParams& params);
void knnSearch(const vector<float>& query,
vector<int>& indices,
vector<float>& dists,
int knn,
const SearchParams& params);
void knnSearch(const Mat& queries,
Mat& indices,
Mat& dists,
int knn,
const SearchParams& params);
int radiusSearch(const vector<float>& query,
vector<int>& indices,
vector<float>& dists,
float radius,
const SearchParams& params);
int radiusSearch(const Mat& query,
Mat& indices,
Mat& dists,
float radius,
const SearchParams& params);
void save(std::string filename);
int veclen() const;
int size() const;
};
}
cv::flann::Index::Index¶
- Index::Index(const Mat& features, const IndexParams& params)¶
Constructs a nearest neighbor search index for a given dataset.
Parameters: - features – Matrix of type CV _ 32F containing the features(points) to index. The size of the matrix is num _ features x feature _ dimensionality.
- params –
Structure containing the index parameters. The type of index that will be constructed depends on the type of this parameter. The possible parameter types are:
- LinearIndexParams When passing an object of this type, the index will perform a linear, brute-force search.
- cvcode
- KDTreeIndexParams When passing an object of this type the index constructed will consist of a set
- of randomized kd-trees which will be searched in parallel.
- cvcode
- trees The number of parallel kd-trees to use. Good values are in the range [1..16]
- KMeansIndexParams When passing an object of this type the index constructed will be a hierarchical k-means tree. cvcode
- branching The branching factor to use for the hierarchical k-means tree
- iterations The maximum number of iterations to use in the k-means clustering
- stage when building the k-means tree. A value of -1 used here means that the k-means clustering should be iterated until convergence
- centers_init The algorithm to use for selecting the initial
centers when performing a k-means clustering step. The possible values are CENTERS _ RANDOM (picks the initial cluster centers randomly), CENTERS _ GONZALES (picks the initial centers using Gonzales’ algorithm) and CENTERS _ KMEANSPP (picks the initial
centers using the algorithm suggested in [arthur_kmeanspp_2007] )
- cb_index This parameter (cluster boundary index) influences the
- way exploration is performed in the hierarchical kmeans tree. When cb_index is zero the next kmeans domain to be explored is choosen to be the one with the closest center. A value greater then zero also takes into account the size of the domain.
- CompositeIndexParams When using a parameters object of this type the index created combines the randomized kd-trees
- and the hierarchical k-means tree. cvcode
- AutotunedIndexParams When passing an object of this type the index created is automatically tuned to offer
- the best performance, by choosing the optimal index type (randomized kd-trees, hierarchical kmeans, linear) and parameters for the
dataset provided. cvcode
- target_precision Is a number between 0 and 1 specifying the
- percentage of the approximate nearest-neighbor searches that return the exact nearest-neighbor. Using a higher value for this parameter gives more accurate results, but the search takes longer. The optimum value usually depends on the application.
- build_weight Specifies the importance of the
- index build time raported to the nearest-neighbor search time. In some applications it’s acceptable for the index build step to take a long time if the subsequent searches in the index can be performed very fast. In other applications it’s required that the index be build as fast as possible even if that leads to slightly longer search times.
- memory_weight Is used to specify the tradeoff between
- time (index build time and search time) and memory used by the index. A value less than 1 gives more importance to the time spent and a value greater than 1 gives more importance to the memory usage.
- sample_fraction Is a number between 0 and 1 indicating what fraction
- of the dataset to use in the automatic parameter configuration algorithm. Running the algorithm on the full dataset gives the most accurate results, but for very large datasets can take longer than desired. In such case using just a fraction of the data helps speeding up this algorithm while still giving good approximations of the optimum parameters.
- SavedIndexParams This object type is used for loading a previously saved index from the disk. cvcode
- filename The filename in which the index was saved.
cv::flann::Index::knnSearch¶
- void Index::knnSearch(const vector<float>& query, vector<int>& indices, vector<float>& dists, int knn, const SearchParams& params)¶
Performs a K-nearest neighbor search for a given query point using the index.
Parameters: - query – The query point
- indices – Vector that will contain the indices of the K-nearest neighbors found. It must have at least knn size.
- dists – Vector that will contain the distances to the K-nearest neighbors found. It must have at least knn size.
- knn – Number of nearest neighbors to search for.
- params – Search parameters
struct SearchParams { SearchParams(int checks = 32); };
- checks The number of times the tree(s) in the index should be recursively traversed. A
higher value for this parameter would give better search precision, but also take more time. If automatic configuration was used when the index was created, the number of checks required to achieve the specified precision was also computed, in which case this parameter is ignored.
cv::flann::Index::knnSearch¶
- void Index::knnSearch(const Mat& queries, Mat& indices, Mat& dists, int knn, const SearchParams& params)
Performs a K-nearest neighbor search for multiple query points.
Parameters: - queries – The query points, one per row
- indices – Indices of the nearest neighbors found
- dists – Distances to the nearest neighbors found
- knn – Number of nearest neighbors to search for
- params – Search parameters
cv::flann::Index::radiusSearch¶
- int Index::radiusSearch(const vector<float>& query, vector<int>& indices, vector<float>& dists, float radius, const SearchParams& params)¶
Performs a radius nearest neighbor search for a given query point.
Parameters: - query – The query point
- indices – Vector that will contain the indices of the points found within the search radius in decreasing order of the distance to the query point. If the number of neighbors in the search radius is bigger than the size of this vector, the ones that don’t fit in the vector are ignored.
- dists – Vector that will contain the distances to the points found within the search radius
- radius – The search radius
- params – Search parameters
cv::flann::Index::radiusSearch¶
- int Index::radiusSearch(const Mat& query, Mat& indices, Mat& dists, float radius, const SearchParams& params)
Performs a radius nearest neighbor search for multiple query points.
Parameters: - queries – The query points, one per row
- indices – Indices of the nearest neighbors found
- dists – Distances to the nearest neighbors found
- radius – The search radius
- params – Search parameters
cv::flann::Index::save¶
- void Index::save(std::string filename)¶
Saves the index to a file.
Parameter: filename – The file to save the index to
cv::flann::hierarchicalClustering¶
- int hierarchicalClustering(const Mat& features, Mat& centers, const KMeansIndexParams& params)¶
Clusters the given points by constructing a hierarchical k-means tree and choosing a cut in the tree that minimizes the cluster’s variance.
Parameters: - features – The points to be clustered
- centers –
The centers of the clusters obtained. The number of rows in this matrix represents the number of clusters desired, however, because of the way the cut in the hierarchical tree is choosen, the number of clusters computed will be
the highest number of the form
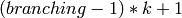 that’s lower than the number of clusters desired, where
that’s lower than the number of clusters desired, where 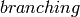 is the tree’s
is the tree’sbranching factor (see description of the KMeansIndexParams).
- params – Parameters used in the construction of the hierarchical k-means tree
The function returns the number of clusters computed.
Help and Feedback
You did not find what you were looking for?- Try the FAQ.
- Ask a question in the user group/mailing list.
- If you think something is missing or wrong in the documentation, please file a bug report.
