Feature Detection¶
cv::Canny¶
- void Canny(const Mat& image, Mat& edges, double threshold1, double threshold2, int apertureSize=3, bool L2gradient=false)¶
Finds edges in an image using Canny algorithm.
Parameters: - image – Single-channel 8-bit input image
- edges – The output edge map. It will have the same size and the same type as image
- threshold1 – The first threshold for the hysteresis procedure
- threshold2 – The second threshold for the hysteresis procedure
- apertureSize – Aperture size for the Sobel() operator
- L2gradient – Indicates, whether the more accurate
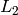 norm
norm 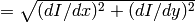 should be used to compute the image gradient magnitude ( L2gradient=true ), or a faster default
should be used to compute the image gradient magnitude ( L2gradient=true ), or a faster default 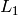 norm
norm 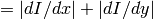 is enough ( L2gradient=false )
is enough ( L2gradient=false )
The function finds edges in the input image image and marks them in the output map edges using the Canny algorithm. The smallest value between threshold1 and threshold2 is used for edge linking, the largest value is used to find the initial segments of strong edges, see http://en.wikipedia.org/wiki/Canny_edge_detector
cv::cornerEigenValsAndVecs¶
- void cornerEigenValsAndVecs(const Mat& src, Mat& dst, int blockSize, int apertureSize, int borderType=BORDER_DEFAULT)¶
Calculates eigenvalues and eigenvectors of image blocks for corner detection.
Parameters: - src – Input single-channel 8-bit or floating-point image
- dst – Image to store the results. It will have the same size as src and the type CV_32FC(6)
- blockSize – Neighborhood size (see discussion)
- apertureSize – Aperture parameter for the Sobel() operator
- boderType – Pixel extrapolation method; see borderInterpolate()
For every pixel
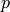 , the function
cornerEigenValsAndVecs
considers a
blockSize
, the function
cornerEigenValsAndVecs
considers a
blockSize
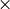 blockSize
neigborhood
blockSize
neigborhood
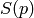 . It calculates the covariation matrix of derivatives over the neighborhood as:
. It calculates the covariation matrix of derivatives over the neighborhood as:
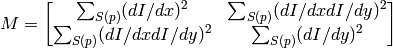
Where the derivatives are computed using Sobel() operator.
After that it finds eigenvectors and eigenvalues of
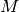 and stores them into destination image in the form
and stores them into destination image in the form
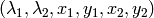 where
where
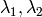
are the eigenvalues of
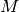 ; not sorted
; not sorted
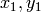
are the eigenvectors corresponding to
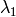
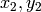
are the eigenvectors corresponding to
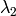
The output of the function can be used for robust edge or corner detection.
See also: cornerMinEigenVal() , cornerHarris() , preCornerDetect()
cv::cornerHarris¶
- void cornerHarris(const Mat& src, Mat& dst, int blockSize, int apertureSize, double k, int borderType=BORDER_DEFAULT)¶
Harris edge detector.
Parameters: - src – Input single-channel 8-bit or floating-point image
- dst – Image to store the Harris detector responses; will have type CV_32FC1 and the same size as src
- blockSize – Neighborhood size (see the discussion of cornerEigenValsAndVecs() )
- apertureSize – Aperture parameter for the Sobel() operator
- k – Harris detector free parameter. See the formula below
- boderType – Pixel extrapolation method; see borderInterpolate()
The function runs the Harris edge detector on the image. Similarly to
cornerMinEigenVal()
and
cornerEigenValsAndVecs()
, for each pixel
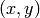 it calculates a
it calculates a
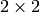 gradient covariation matrix
gradient covariation matrix
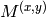 over a
over a
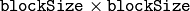 neighborhood. Then, it computes the following characteristic:
neighborhood. Then, it computes the following characteristic:
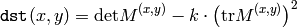
Corners in the image can be found as the local maxima of this response map.
cv::cornerMinEigenVal¶
- void cornerMinEigenVal(const Mat& src, Mat& dst, int blockSize, int apertureSize=3, int borderType=BORDER_DEFAULT)¶
Calculates the minimal eigenvalue of gradient matrices for corner detection.
Parameters: - src – Input single-channel 8-bit or floating-point image
- dst – Image to store the minimal eigenvalues; will have type CV_32FC1 and the same size as src
- blockSize – Neighborhood size (see the discussion of cornerEigenValsAndVecs() )
- apertureSize – Aperture parameter for the Sobel() operator
- boderType – Pixel extrapolation method; see borderInterpolate()
The function is similar to
cornerEigenValsAndVecs()
but it calculates and stores only the minimal eigenvalue of the covariation matrix of derivatives, i.e.
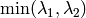 in terms of the formulae in
cornerEigenValsAndVecs()
description.
in terms of the formulae in
cornerEigenValsAndVecs()
description.
cv::cornerSubPix¶
- void cornerSubPix(const Mat& image, vector<Point2f>& corners, Size winSize, Size zeroZone, TermCriteria criteria)¶
Refines the corner locations.
Parameters: - image – Input image
- corners – Initial coordinates of the input corners; refined coordinates on output
- winSize – Half of the side length of the search window. For example, if winSize=Size(5,5) , then a
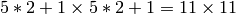 search window would be used
search window would be used - zeroZone – Half of the size of the dead region in the middle of the search zone over which the summation in the formula below is not done. It is used sometimes to avoid possible singularities of the autocorrelation matrix. The value of (-1,-1) indicates that there is no such size
- criteria – Criteria for termination of the iterative process of corner refinement. That is, the process of corner position refinement stops either after a certain number of iterations or when a required accuracy is achieved. The criteria may specify either of or both the maximum number of iteration and the required accuracy
The function iterates to find the sub-pixel accurate location of corners, or radial saddle points, as shown in on the picture below.
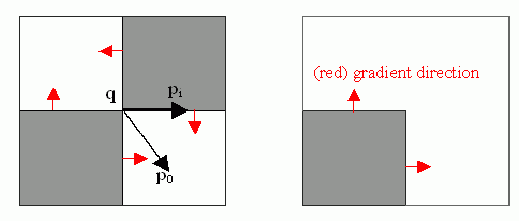
Sub-pixel accurate corner locator is based on the observation that every vector from the center
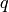 to a point
to a point
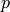 located within a neighborhood of
located within a neighborhood of
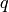 is orthogonal to the image gradient at
is orthogonal to the image gradient at
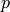 subject to image and measurement noise. Consider the expression:
subject to image and measurement noise. Consider the expression:
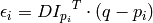
where
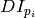 is the image gradient at the one of the points
is the image gradient at the one of the points
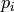 in a neighborhood of
in a neighborhood of
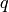 . The value of
. The value of
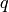 is to be found such that
is to be found such that
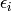 is minimized. A system of equations may be set up with
is minimized. A system of equations may be set up with
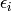 set to zero:
set to zero:
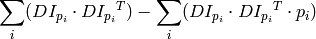
where the gradients are summed within a neighborhood (“search window”) of
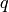 . Calling the first gradient term
. Calling the first gradient term
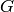 and the second gradient term
and the second gradient term
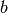 gives:
gives:
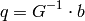
The algorithm sets the center of the neighborhood window at this new center
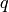 and then iterates until the center keeps within a set threshold.
and then iterates until the center keeps within a set threshold.
cv::goodFeaturesToTrack¶
- void goodFeaturesToTrack(const Mat& image, vector<Point2f>& corners, int maxCorners, double qualityLevel, double minDistance, const Mat& mask=Mat(), int blockSize=3, bool useHarrisDetector=false, double k=0.04)¶
Determines strong corners on an image.
Parameters: - image – The input 8-bit or floating-point 32-bit, single-channel image
- corners – The output vector of detected corners
- maxCorners – The maximum number of corners to return. If there are more corners than that will be found, the strongest of them will be returned
- qualityLevel – Characterizes the minimal accepted quality of image corners; the value of the parameter is multiplied by the by the best corner quality measure (which is the min eigenvalue, see cornerMinEigenVal() , or the Harris function response, see cornerHarris() ). The corners, which quality measure is less than the product, will be rejected. For example, if the best corner has the quality measure = 1500, and the qualityLevel=0.01 , then all the corners which quality measure is less than 15 will be rejected.
- minDistance – The minimum possible Euclidean distance between the returned corners
- mask – The optional region of interest. If the image is not empty (then it needs to have the type CV_8UC1 and the same size as image ), it will specify the region in which the corners are detected
- blockSize – Size of the averaging block for computing derivative covariation matrix over each pixel neighborhood, see cornerEigenValsAndVecs()
- useHarrisDetector – Indicates, whether to use operator or cornerMinEigenVal()
- k – Free parameter of Harris detector
The function finds the most prominent corners in the image or in the specified image region, as described in Shi94 :
- the function first calculates the corner quality measure at every source image pixel using the cornerMinEigenVal() or cornerHarris()
- then it performs non-maxima suppression (the local maxima in
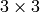 neighborhood
are retained).
neighborhood
are retained). - the next step rejects the corners with the minimal eigenvalue less than
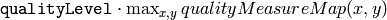 .
. - the remaining corners are then sorted by the quality measure in the descending order.
- finally, the function throws away each corner
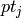 if there is a stronger corner
if there is a stronger corner
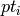 (
(
 ) such that the distance between them is less than
minDistance
) such that the distance between them is less than
minDistance
The function can be used to initialize a point-based tracker of an object.
Note that the if the function is called with different values A and B of the parameter qualityLevel , and A > {B}, the vector of returned corners with qualityLevel=A will be the prefix of the output vector with qualityLevel=B .
See also: cornerMinEigenVal() , cornerHarris() , calcOpticalFlowPyrLK() , estimateRigidMotion() , PlanarObjectDetector() , OneWayDescriptor()
cv::HoughCircles¶
- void HoughCircles(Mat& image, vector<Vec3f>& circles, int method, double dp, double minDist, double param1=100, double param2=100, int minRadius=0, int maxRadius=0)¶
Finds circles in a grayscale image using a Hough transform.
Parameters: - image – The 8-bit, single-channel, grayscale input image
- circles – The output vector of found circles. Each vector is encoded as 3-element floating-point vector
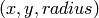
- method – Currently, the only implemented method is CV_HOUGH_GRADIENT , which is basically 21HT , described in Yuen90 .
- dp – The inverse ratio of the accumulator resolution to the image resolution. For example, if dp=1 , the accumulator will have the same resolution as the input image, if dp=2 - accumulator will have half as big width and height, etc
- minDist – Minimum distance between the centers of the detected circles. If the parameter is too small, multiple neighbor circles may be falsely detected in addition to a true one. If it is too large, some circles may be missed
- param1 – The first method-specific parameter. in the case of CV_HOUGH_GRADIENT it is the higher threshold of the two passed to Canny() edge detector (the lower one will be twice smaller)
- param2 – The second method-specific parameter. in the case of CV_HOUGH_GRADIENT it is the accumulator threshold at the center detection stage. The smaller it is, the more false circles may be detected. Circles, corresponding to the larger accumulator values, will be returned first
- minRadius – Minimum circle radius
- maxRadius – Maximum circle radius
The function finds circles in a grayscale image using some modification of Hough transform. Here is a short usage example:
#include <cv.h>
#include <highgui.h>
#include <math.h>
using namespace cv;
int main(int argc, char** argv)
{
Mat img, gray;
if( argc != 2 && !(img=imread(argv[1], 1)).data)
return -1;
cvtColor(img, gray, CV_BGR2GRAY);
// smooth it, otherwise a lot of false circles may be detected
GaussianBlur( gray, gray, Size(9, 9), 2, 2 );
vector<Vec3f> circles;
HoughCircles(gray, circles, CV_HOUGH_GRADIENT,
2, gray->rows/4, 200, 100 );
for( size_t i = 0; i < circles.size(); i++ )
{
Point center(cvRound(circles[i][0]), cvRound(circles[i][1]));
int radius = cvRound(circles[i][2]);
// draw the circle center
circle( img, center, 3, Scalar(0,255,0), -1, 8, 0 );
// draw the circle outline
circle( img, center, radius, Scalar(0,0,255), 3, 8, 0 );
}
namedWindow( "circles", 1 );
imshow( "circles", img );
return 0;
}
Note that usually the function detects the circles’ centers well, however it may fail to find the correct radii. You can assist the function by specifying the radius range ( minRadius and maxRadius ) if you know it, or you may ignore the returned radius, use only the center and find the correct radius using some additional procedure.
See also: fitEllipse() , minEnclosingCircle()
cv::HoughLines¶
- void HoughLines(Mat& image, vector<Vec2f>& lines, double rho, double theta, int threshold, double srn=0, double stn=0)¶
Finds lines in a binary image using standard Hough transform.
Parameters: - image – The 8-bit, single-channel, binary source image. The image may be modified by the function
- lines – The output vector of lines. Each line is represented by a two-element vector
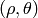 .
. 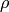 is the distance from the coordinate origin
is the distance from the coordinate origin 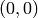 (top-left corner of the image) and
(top-left corner of the image) and 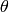 is the line rotation angle in radians (
is the line rotation angle in radians ( 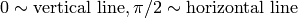 )
) - rho – Distance resolution of the accumulator in pixels
- theta – Angle resolution of the accumulator in radians
- threshold – The accumulator threshold parameter. Only those lines are returned that get enough votes (
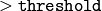 )
) - srn – For the multi-scale Hough transform it is the divisor for the distance resolution rho . The coarse accumulator distance resolution will be rho and the accurate accumulator resolution will be rho/srn . If both srn=0 and stn=0 then the classical Hough transform is used, otherwise both these parameters should be positive.
- stn – For the multi-scale Hough transform it is the divisor for the distance resolution theta
The function implements standard or standard multi-scale Hough transform algorithm for line detection. See HoughLinesP() for the code example.
cv::HoughLinesP¶
- void HoughLinesP(Mat& image, vector<Vec4i>& lines, double rho, double theta, int threshold, double minLineLength=0, double maxLineGap=0)¶
Finds lines segments in a binary image using probabilistic Hough transform.
Parameters: - image – The 8-bit, single-channel, binary source image. The image may be modified by the function
- lines – The output vector of lines. Each line is represented by a 4-element vector
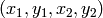 , where
, where 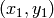 and
and 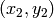 are the ending points of each line segment detected.
are the ending points of each line segment detected. - rho – Distance resolution of the accumulator in pixels
- theta – Angle resolution of the accumulator in radians
- threshold – The accumulator threshold parameter. Only those lines are returned that get enough votes (
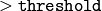 )
) - minLineLength – The minimum line length. Line segments shorter than that will be rejected
- maxLineGap – The maximum allowed gap between points on the same line to link them.
The function implements probabilistic Hough transform algorithm for line detection, described in Matas00 . Below is line detection example:
/* This is a standalone program. Pass an image name as a first parameter
of the program. Switch between standard and probabilistic Hough transform
by changing "#if 1" to "#if 0" and back */
#include <cv.h>
#include <highgui.h>
#include <math.h>
using namespace cv;
int main(int argc, char** argv)
{
Mat src, dst, color_dst;
if( argc != 2 || !(src=imread(argv[1], 0)).data)
return -1;
Canny( src, dst, 50, 200, 3 );
cvtColor( dst, color_dst, CV_GRAY2BGR );
#if 0
vector<Vec2f> lines;
HoughLines( dst, lines, 1, CV_PI/180, 100 );
for( size_t i = 0; i < lines.size(); i++ )
{
float rho = lines[i][0];
float theta = lines[i][1];
double a = cos(theta), b = sin(theta);
double x0 = a*rho, y0 = b*rho;
Point pt1(cvRound(x0 + 1000*(-b)),
cvRound(y0 + 1000*(a)));
Point pt2(cvRound(x0 - 1000*(-b)),
cvRound(y0 - 1000*(a)));
line( color_dst, pt1, pt2, Scalar(0,0,255), 3, 8 );
}
#else
vector<Vec4i> lines;
HoughLinesP( dst, lines, 1, CV_PI/180, 80, 30, 10 );
for( size_t i = 0; i < lines.size(); i++ )
{
line( color_dst, Point(lines[i][0], lines[i][1]),
Point(lines[i][2], lines[i][3]), Scalar(0,0,255), 3, 8 );
}
#endif
namedWindow( "Source", 1 );
imshow( "Source", src );
namedWindow( "Detected Lines", 1 );
imshow( "Detected Lines", color_dst );
waitKey(0);
return 0;
}
This is the sample picture the function parameters have been tuned for:

And this is the output of the above program in the case of probabilistic Hough transform

cv::preCornerDetect¶
- void preCornerDetect(const Mat& src, Mat& dst, int apertureSize, int borderType=BORDER_DEFAULT)¶
Calculates the feature map for corner detection
Parameters: - src – The source single-channel 8-bit of floating-point image
- dst – The output image; will have type CV_32F and the same size as src
- apertureSize – Aperture size of Sobel()
- borderType – The pixel extrapolation method; see borderInterpolate()
The function calculates the complex spatial derivative-based function of the source image
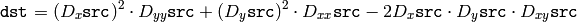
where
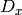 ,
,
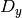 are the first image derivatives,
are the first image derivatives,
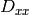 ,
,
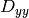 are the second image derivatives and
are the second image derivatives and
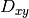 is the mixed derivative.
is the mixed derivative.
The corners can be found as local maximums of the functions, as shown below:
Mat corners, dilated_corners;
preCornerDetect(image, corners, 3);
// dilation with 3x3 rectangular structuring element
dilate(corners, dilated_corners, Mat(), 1);
Mat corner_mask = corners == dilated_corners;
Help and Feedback
You did not find what you were looking for?- Try the Cheatsheet.
- Ask a question in the user group/mailing list.
- If you think something is missing or wrong in the documentation, please file a bug report.
