Geometric Image Transformations¶
The functions in this section perform various geometrical transformations of 2D images. That is, they do not change the image content, but deform the pixel grid, and map this deformed grid to the destination image. In fact, to avoid sampling artifacts, the mapping is done in the reverse order, from destination to the source. That is, for each pixel
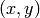 of the destination image, the functions compute coordinates of the corresponding “donor” pixel in the source image and copy the pixel value, that is:
of the destination image, the functions compute coordinates of the corresponding “donor” pixel in the source image and copy the pixel value, that is:
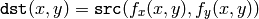
In the case when the user specifies the forward mapping:
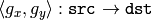 , the OpenCV functions first compute the corresponding inverse mapping:
, the OpenCV functions first compute the corresponding inverse mapping:
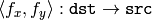 and then use the above formula.
and then use the above formula.
The actual implementations of the geometrical transformations, from the most generic Remap and to the simplest and the fastest Resize , need to solve the 2 main problems with the above formula:
- extrapolation of non-existing pixels. Similarly to the filtering functions, described in the previous section, for some
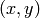 one of
one of
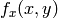 or
or
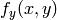 , or they both, may fall outside of the image, in which case some extrapolation method needs to be used. OpenCV provides the same selection of the extrapolation methods as in the filtering functions, but also an additional method
BORDER_TRANSPARENT
, which means that the corresponding pixels in the destination image will not be modified at all.
, or they both, may fall outside of the image, in which case some extrapolation method needs to be used. OpenCV provides the same selection of the extrapolation methods as in the filtering functions, but also an additional method
BORDER_TRANSPARENT
, which means that the corresponding pixels in the destination image will not be modified at all. - interpolation of pixel values. Usually
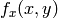 and
and
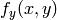 are floating-point numbers (i.e.
are floating-point numbers (i.e.
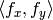 can be an affine or perspective transformation, or radial lens distortion correction etc.), so a pixel values at fractional coordinates needs to be retrieved. In the simplest case the coordinates can be just rounded to the nearest integer coordinates and the corresponding pixel used, which is called nearest-neighbor interpolation. However, a better result can be achieved by using more sophisticated
interpolation methods
, where a polynomial function is fit into some neighborhood of the computed pixel
can be an affine or perspective transformation, or radial lens distortion correction etc.), so a pixel values at fractional coordinates needs to be retrieved. In the simplest case the coordinates can be just rounded to the nearest integer coordinates and the corresponding pixel used, which is called nearest-neighbor interpolation. However, a better result can be achieved by using more sophisticated
interpolation methods
, where a polynomial function is fit into some neighborhood of the computed pixel
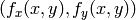 and then the value of the polynomial at
and then the value of the polynomial at
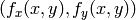 is taken as the interpolated pixel value. In OpenCV you can choose between several interpolation methods, see
Resize
.
is taken as the interpolated pixel value. In OpenCV you can choose between several interpolation methods, see
Resize
.
cv::convertMaps¶
- void convertMaps(const Mat& map1, const Mat& map2, Mat& dstmap1, Mat& dstmap2, int dstmap1type, bool nninterpolation=false)¶
Converts image transformation maps from one representation to another
Parameters: - map1 – The first input map of type CV_16SC2 or CV_32FC1 or CV_32FC2
- map2 – The second input map of type CV_16UC1 or CV_32FC1 or none (empty matrix), respectively
- dstmap1 – The first output map; will have type dstmap1type and the same size as src
- dstmap2 – The second output map
- dstmap1type – The type of the first output map; should be CV_16SC2 , CV_32FC1 or CV_32FC2
- nninterpolation – Indicates whether the fixed-point maps will be used for nearest-neighbor or for more complex interpolation
The function converts a pair of maps for
remap()
from one representation to another. The following options (
(map1.type(), map2.type())
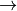 (dstmap1.type(), dstmap2.type())
) are supported:
(dstmap1.type(), dstmap2.type())
) are supported:
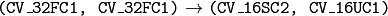 . This is the most frequently used conversion operation, in which the original floating-point maps (see
remap()
) are converted to more compact and much faster fixed-point representation. The first output array will contain the rounded coordinates and the second array (created only when
nninterpolation=false
) will contain indices in the interpolation tables.
. This is the most frequently used conversion operation, in which the original floating-point maps (see
remap()
) are converted to more compact and much faster fixed-point representation. The first output array will contain the rounded coordinates and the second array (created only when
nninterpolation=false
) will contain indices in the interpolation tables.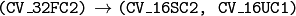 . The same as above, but the original maps are stored in one 2-channel matrix.
. The same as above, but the original maps are stored in one 2-channel matrix.- the reverse conversion. Obviously, the reconstructed floating-point maps will not be exactly the same as the originals.
See also: remap() , undisort() , initUndistortRectifyMap()
cv::getAffineTransform¶
- Mat getAffineTransform(const Point2f src[], const Point2f dst[])¶
Calculates the affine transform from 3 pairs of the corresponding points
Parameters: - src – Coordinates of a triangle vertices in the source image
- dst – Coordinates of the corresponding triangle vertices in the destination image
The function calculates the
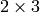 matrix of an affine transform such that:
matrix of an affine transform such that:

where
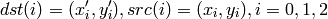
See also: warpAffine() , transform()
cv::getPerspectiveTransform¶
- Mat getPerspectiveTransform(const Point2f src[], const Point2f dst[])¶
Calculates the perspective transform from 4 pairs of the corresponding points
Parameters: - src – Coordinates of a quadrange vertices in the source image
- dst – Coordinates of the corresponding quadrangle vertices in the destination image
The function calculates the
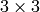 matrix of a perspective transform such that:
matrix of a perspective transform such that:

where
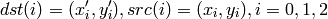
See also: findHomography() , warpPerspective() , perspectiveTransform()
cv::getRectSubPix¶
- void getRectSubPix(const Mat& image, Size patchSize, Point2f center, Mat& dst, int patchType=-1)¶
Retrieves the pixel rectangle from an image with sub-pixel accuracy
Parameters: - src – Source image
- patchSize – Size of the extracted patch
- center – Floating point coordinates of the extracted rectangle center within the source image. The center must be inside the image
- dst – The extracted patch; will have the size patchSize and the same number of channels as src
- patchType – The depth of the extracted pixels. By default they will have the same depth as src
The function getRectSubPix extracts pixels from src :
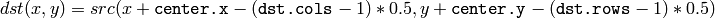
where the values of the pixels at non-integer coordinates are retrieved using bilinear interpolation. Every channel of multiple-channel images is processed independently. While the rectangle center must be inside the image, parts of the rectangle may be outside. In this case, the replication border mode (see borderInterpolate() ) is used to extrapolate the pixel values outside of the image.
See also: warpAffine() , warpPerspective()
cv::getRotationMatrix2D¶
- Mat getRotationMatrix2D(Point2f center, double angle, double scale)¶
Calculates the affine matrix of 2d rotation.
Parameters: - center – Center of the rotation in the source image
- angle – The rotation angle in degrees. Positive values mean counter-clockwise rotation (the coordinate origin is assumed to be the top-left corner)
- scale – Isotropic scale factor
The function calculates the following matrix:
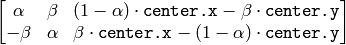
where
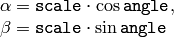
The transformation maps the rotation center to itself. If this is not the purpose, the shift should be adjusted.
See also: getAffineTransform() , warpAffine() , transform()
cv::invertAffineTransform¶
- void invertAffineTransform(const Mat& M, Mat& iM)¶
Inverts an affine transformation
Parameters: - M – The original affine transformation
- iM – The output reverse affine transformation
The function computes inverse affine transformation represented by
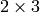 matrix
M
:
matrix
M
:
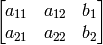
The result will also be a
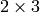 matrix of the same type as
M
.
matrix of the same type as
M
.
cv::remap¶
- void remap(const Mat& src, Mat& dst, const Mat& map1, const Mat& map2, int interpolation, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())¶
Applies a generic geometrical transformation to an image.
Parameters: - src – Source image
- dst – Destination image. It will have the same size as map1 and the same type as src
- map1 – The first map of either (x,y) points or just x values having type CV_16SC2 , CV_32FC1 or CV_32FC2 . See convertMaps() for converting floating point representation to fixed-point for speed.
- map2 – The second map of y values having type CV_16UC1 , CV_32FC1 or none (empty map if map1 is (x,y) points), respectively
- interpolation – The interpolation method, see resize() . The method INTER_AREA is not supported by this function
- borderMode – The pixel extrapolation method, see borderInterpolate() . When the borderMode=BORDER_TRANSPARENT , it means that the pixels in the destination image that corresponds to the “outliers” in the source image are not modified by the function
- borderValue – A value used in the case of a constant border. By default it is 0
The function remap transforms the source image using the specified map:
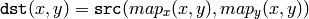
Where values of pixels with non-integer coordinates are computed using one of the available interpolation methods.
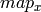 and
and
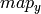 can be encoded as separate floating-point maps in
can be encoded as separate floating-point maps in
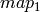 and
and
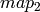 respectively, or interleaved floating-point maps of
respectively, or interleaved floating-point maps of
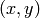 in
in
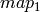 , or
fixed-point maps made by using
convertMaps()
. The reason you might want to convert from floating to fixed-point
representations of a map is that they can yield much faster (~2x) remapping operations. In the converted case,
, or
fixed-point maps made by using
convertMaps()
. The reason you might want to convert from floating to fixed-point
representations of a map is that they can yield much faster (~2x) remapping operations. In the converted case,
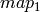 contains pairs
(cvFloor(x), cvFloor(y))
and
contains pairs
(cvFloor(x), cvFloor(y))
and
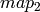 contains indices in a table of interpolation coefficients.
contains indices in a table of interpolation coefficients.
This function can not operate in-place.
cv::resize¶
- void resize(const Mat& src, Mat& dst, Size dsize, double fx=0, double fy=0, int interpolation=INTER_LINEAR)¶
Resizes an image
Parameters: - src – Source image
- dst – Destination image. It will have size dsize (when it is non-zero) or the size computed from src.size() and fx and fy . The type of dst will be the same as of src .
- dsize –
The destination image size. If it is zero, then it is computed as:
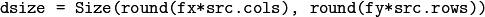
. Either dsize or both fx or fy must be non-zero.
- fx –
The scale factor along the horizontal axis. When 0, it is computed as
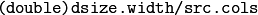
- fy –
The scale factor along the vertical axis. When 0, it is computed as
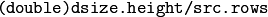
- interpolation –
The interpolation method:
- INTER_NEAREST nearest-neighbor interpolation
- INTER_LINEAR bilinear interpolation (used by default)
- INTER_AREA resampling using pixel area relation. It may be the preferred method for image decimation, as it gives moire-free results. But when the image is zoomed, it is similar to the INTER_NEAREST method
- INTER_CUBIC bicubic interpolation over 4x4 pixel neighborhood
- INTER_LANCZOS4 Lanczos interpolation over 8x8 pixel neighborhood
The function resize resizes an image src down to or up to the specified size. Note that the initial dst type or size are not taken into account. Instead the size and type are derived from the src , dsize , fx and fy . If you want to resize src so that it fits the pre-created dst , you may call the function as:
// explicitly specify dsize=dst.size(); fx and fy will be computed from that.
resize(src, dst, dst.size(), 0, 0, interpolation);
If you want to decimate the image by factor of 2 in each direction, you can call the function this way:
// specify fx and fy and let the function to compute the destination image size.
resize(src, dst, Size(), 0.5, 0.5, interpolation);
See also: warpAffine() , warpPerspective() , remap() .
cv::warpAffine¶
- void warpAffine(const Mat& src, Mat& dst, const Mat& M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())¶
Applies an affine transformation to an image.
Parameters: - src – Source image
- dst – Destination image; will have size dsize and the same type as src
- M –
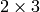 transformation matrix
transformation matrix - dsize – Size of the destination image
- flags – A combination of interpolation methods, see resize() , and the optional flag WARP_INVERSE_MAP that means that M is the inverse transformation (
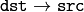 )
) - borderMode – The pixel extrapolation method, see borderInterpolate() . When the borderMode=BORDER_TRANSPARENT , it means that the pixels in the destination image that corresponds to the “outliers” in the source image are not modified by the function
- borderValue – A value used in case of a constant border. By default it is 0
The function warpAffine transforms the source image using the specified matrix:
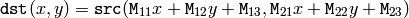
when the flag WARP_INVERSE_MAP is set. Otherwise, the transformation is first inverted with invertAffineTransform() and then put in the formula above instead of M . The function can not operate in-place.
See also: warpPerspective() , resize() , remap() , getRectSubPix() , transform()
cv::warpPerspective¶
- void warpPerspective(const Mat& src, Mat& dst, const Mat& M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())¶
Applies a perspective transformation to an image.
Parameters: - src – Source image
- dst – Destination image; will have size dsize and the same type as src
- M –
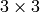 transformation matrix
transformation matrix - dsize – Size of the destination image
- flags – A combination of interpolation methods, see resize() , and the optional flag WARP_INVERSE_MAP that means that M is the inverse transformation (
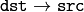 )
) - borderMode – The pixel extrapolation method, see borderInterpolate() . When the borderMode=BORDER_TRANSPARENT , it means that the pixels in the destination image that corresponds to the “outliers” in the source image are not modified by the function
- borderValue – A value used in case of a constant border. By default it is 0
The function warpPerspective transforms the source image using the specified matrix:
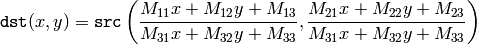
when the flag WARP_INVERSE_MAP is set. Otherwise, the transformation is first inverted with invert() and then put in the formula above instead of M . The function can not operate in-place.
See also: warpAffine() , resize() , remap() , getRectSubPix() , perspectiveTransform()
Help and Feedback
You did not find what you were looking for?- Try the Cheatsheet.
- Ask a question in the user group/mailing list.
- If you think something is missing or wrong in the documentation, please file a bug report.
