Basic Structures¶

DataType¶

Template “traits” class for other OpenCV primitive data types

template<typename _Tp> class DataType
{
    // value_type is always a synonym for _Tp.
    typedef _Tp value_type;

    // intermediate type used for operations on _Tp.
    // it is int for uchar, signed char, unsigned short, signed short and int,
    // float for float, double for double, ...
    typedef <...> work_type;
    // in the case of multi-channel data it is the data type of each channel
    typedef <...> channel_type;
    enum
    {
        // CV_8U ... CV_64F
        depth = DataDepth<channel_type>::value,
        // 1 ...
        channels = <...>,
        // '1u', '4i', '3f', '2d' etc.
        fmt=<...>,
        // CV_8UC3, CV_32FC2 ...
        type = CV_MAKETYPE(depth, channels)
    };
};

The template class DataType is descriptive class for OpenCV primitive data types and other types that comply with the following definition. A primitive OpenCV data type is one of unsigned char, bool, signed char, unsigned short, signed short, int, float, double or a tuple of values of one of these types, where all the values in the tuple have the same type. If you are familiar with OpenCV CvMat ‘s type notation, CV _ 8U ... CV _ 32FC3, CV _ 64FC2 etc., then a primitive type can be defined as a type for which you can give a unique identifier in a form CV_<bit-depth>{U|S|F}C<number_of_channels> . A universal OpenCV structure able to store a single instance of such primitive data type is Vec . Multiple instances of such a type can be stored to a std::vector , Mat , Mat_ , SparseMat , SparseMat_ or any other container that is able to store Vec instances.

The class DataType is basically used to provide some description of such primitive data types without adding any fields or methods to the corresponding classes (and it is actually impossible to add anything to primitive C/C++ data types). This technique is known in C++ as class traits. It’s not DataType itself that is used, but its specialized versions, such as:

template<> class DataType<uchar>
{
    typedef uchar value_type;
    typedef int work_type;
    typedef uchar channel_type;
    enum { channel_type = CV_8U, channels = 1, fmt='u', type = CV_8U };
};
...
template<typename _Tp> DataType<std::complex<_Tp> >
{
    typedef std::complex<_Tp> value_type;
    typedef std::complex<_Tp> work_type;
    typedef _Tp channel_type;
    // DataDepth is another helper trait class
    enum { depth = DataDepth<_Tp>::value, channels=2,
        fmt=(channels-1)*256+DataDepth<_Tp>::fmt,
        type=CV_MAKETYPE(depth, channels) };
};
...

The main purpose of the classes is to convert compile-time type information to OpenCV-compatible data type identifier, for example:

// allocates 30x40 floating-point matrix
Mat A(30, 40, DataType<float>::type);

Mat B = Mat_<std::complex<double> >(3, 3);
// the statement below will print 6, 2 /* i.e. depth == CV_64F, channels == 2 */
cout << B.depth() << ", " << B.channels() << endl;

that is, such traits are used to tell OpenCV which data type you are working with, even if such a type is not native to OpenCV (the matrix B intialization above compiles because OpenCV defines the proper specialized template class DataType<complex<_Tp> > ). Also, this mechanism is useful (and used in OpenCV this way) for generic algorithms implementations.

Point_¶

Template class for 2D points

template<typename _Tp> class Point_
{
public:
    typedef _Tp value_type;

    Point_();
    Point_(_Tp _x, _Tp _y);
    Point_(const Point_& pt);
    Point_(const CvPoint& pt);
    Point_(const CvPoint2D32f& pt);
    Point_(const Size_<_Tp>& sz);
    Point_(const Vec<_Tp, 2>& v);
    Point_& operator = (const Point_& pt);
    template<typename _Tp2> operator Point_<_Tp2>() const;
    operator CvPoint() const;
    operator CvPoint2D32f() const;
    operator Vec<_Tp, 2>() const;

    // computes dot-product (this->x*pt.x + this->y*pt.y)
    _Tp dot(const Point_& pt) const;
    // computes dot-product using double-precision arithmetics
    double ddot(const Point_& pt) const;
    // returns true if the point is inside the rectangle "r".
    bool inside(const Rect_<_Tp>& r) const;

    _Tp x, y;
};

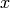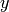The class represents a 2D point, specified by its coordinates $x$ and $y$ . Instance of the class is interchangeable with C structures CvPoint and CvPoint2D32f . There is also cast operator to convert point coordinates to the specified type. The conversion from floating-point coordinates to integer coordinates is done by rounding; in general case the conversion uses operation on each of the coordinates. Besides the class members listed in the declaration above, the following operations on points are implemented:

pt1 = pt2 + pt3;
pt1 = pt2 - pt3;
pt1 = pt2 * a;
pt1 = a * pt2;
pt1 += pt2;
pt1 -= pt2;
pt1 *= a;
double value = norm(pt); // L2 norm
pt1 == pt2;
pt1 != pt2;

For user convenience, the following type aliases are defined:

typedef Point_<int> Point2i;
typedef Point2i Point;
typedef Point_<float> Point2f;
typedef Point_<double> Point2d;

Here is a short example:

Point2f a(0.3f, 0.f), b(0.f, 0.4f);
Point pt = (a + b)*10.f;
cout << pt.x << ", " << pt.y << endl;

Point3_¶

Template class for 3D points

template<typename _Tp> class Point3_
{
public:
    typedef _Tp value_type;

    Point3_();
    Point3_(_Tp _x, _Tp _y, _Tp _z);
    Point3_(const Point3_& pt);
    explicit Point3_(const Point_<_Tp>& pt);
    Point3_(const CvPoint3D32f& pt);
    Point3_(const Vec<_Tp, 3>& v);
    Point3_& operator = (const Point3_& pt);
    template<typename _Tp2> operator Point3_<_Tp2>() const;
    operator CvPoint3D32f() const;
    operator Vec<_Tp, 3>() const;

    _Tp dot(const Point3_& pt) const;
    double ddot(const Point3_& pt) const;

    _Tp x, y, z;
};

The class represents a 3D point, specified by its coordinates 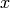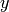$x$ , $y$ and $z$ . Instance of the class is interchangeable with C structure CvPoint2D32f . Similarly to Point_ , the 3D points’ coordinates can be converted to another type, and the vector arithmetic and comparison operations are also supported.

The following type aliases are available:

typedef Point3_<int> Point3i;
typedef Point3_<float> Point3f;
typedef Point3_<double> Point3d;

Size_¶

Template class for specfying image or rectangle size.

template<typename _Tp> class Size_
{
public:
    typedef _Tp value_type;

    Size_();
    Size_(_Tp _width, _Tp _height);
    Size_(const Size_& sz);
    Size_(const CvSize& sz);
    Size_(const CvSize2D32f& sz);
    Size_(const Point_<_Tp>& pt);
    Size_& operator = (const Size_& sz);
    _Tp area() const;

    operator Size_<int>() const;
    operator Size_<float>() const;
    operator Size_<double>() const;
    operator CvSize() const;
    operator CvSize2D32f() const;

    _Tp width, height;
};

The class Size_ is similar to Point_ , except that the two members are called width and height instead of x and y . The structure can be converted to and from the old OpenCV structures CvSize and CvSize2D32f . The same set of arithmetic and comparison operations as for Point_ is available.

OpenCV defines the following type aliases:

typedef Size_<int> Size2i;
typedef Size2i Size;
typedef Size_<float> Size2f;

Rect_¶

Template class for 2D rectangles

template<typename _Tp> class Rect_
{
public:
    typedef _Tp value_type;

    Rect_();
    Rect_(_Tp _x, _Tp _y, _Tp _width, _Tp _height);
    Rect_(const Rect_& r);
    Rect_(const CvRect& r);
    // (x, y) <- org, (width, height) <- sz
    Rect_(const Point_<_Tp>& org, const Size_<_Tp>& sz);
    // (x, y) <- min(pt1, pt2), (width, height) <- max(pt1, pt2) - (x, y)
    Rect_(const Point_<_Tp>& pt1, const Point_<_Tp>& pt2);
    Rect_& operator = ( const Rect_& r );
    // returns Point_<_Tp>(x, y)
    Point_<_Tp> tl() const;
    // returns Point_<_Tp>(x+width, y+height)
    Point_<_Tp> br() const;

    // returns Size_<_Tp>(width, height)
    Size_<_Tp> size() const;
    // returns width*height
    _Tp area() const;

    operator Rect_<int>() const;
    operator Rect_<float>() const;
    operator Rect_<double>() const;
    operator CvRect() const;

    // x <= pt.x && pt.x < x + width &&
    // y <= pt.y && pt.y < y + height ? true : false
    bool contains(const Point_<_Tp>& pt) const;

    _Tp x, y, width, height;
};

The rectangle is described by the coordinates of the top-left corner (which is the default interpretation of Rect_::x and Rect_::y in OpenCV; though, in your algorithms you may count x and y from the bottom-left corner), the rectangle width and height.

Another assumption OpenCV usually makes is that the top and left boundary of the rectangle are inclusive, while the right and bottom boundaries are not, for example, the method Rect_::contains returns true if

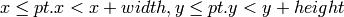
$x \leq pt.x < x+width, y \leq pt.y < y+height$

And virtually every loop over an image ROI in OpenCV (where ROI is specified by Rect_<int> ) is implemented as:

for(int y = roi.y; y < roi.y + rect.height; y++)
    for(int x = roi.x; x < roi.x + rect.width; x++)
    {
        // ...
    }

In addition to the class members, the following operations on rectangles are implemented:

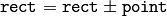$\texttt{rect} = \texttt{rect} \pm \texttt{point}$ (shifting rectangle by a certain offset)
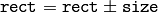$\texttt{rect} = \texttt{rect} \pm \texttt{size}$ (expanding or shrinking rectangle by a certain amount)
rect += point, rect -= point, rect += size, rect -= size (augmenting operations)
rect = rect1 & rect2 (rectangle intersection)
rect = rect1 | rect2 (minimum area rectangle containing rect2 and rect3 )
rect &= rect1, rect |= rect1 (and the corresponding augmenting operations)
rect == rect1, rect != rect1 (rectangle comparison)

Example. Here is how the partial ordering on rectangles can be established (rect1 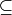$\subseteq$ rect2):

template<typename _Tp> inline bool
operator <= (const Rect_<_Tp>& r1, const Rect_<_Tp>& r2)
{
    return (r1 & r2) == r1;
}

For user convenience, the following type alias is available:

typedef Rect_<int> Rect;

RotatedRect¶

Possibly rotated rectangle

class RotatedRect
{
public:
    // constructors
    RotatedRect();
    RotatedRect(const Point2f& _center, const Size2f& _size, float _angle);
    RotatedRect(const CvBox2D& box);

    // returns minimal up-right rectangle that contains the rotated rectangle
    Rect boundingRect() const;
    // backward conversion to CvBox2D
    operator CvBox2D() const;

    // mass center of the rectangle
    Point2f center;
    // size
    Size2f size;
    // rotation angle in degrees
    float angle;
};

The class RotatedRect replaces the old CvBox2D and fully compatible with it.

TermCriteria¶

Termination criteria for iterative algorithms

class TermCriteria
{
public:
    enum { COUNT=1, MAX_ITER=COUNT, EPS=2 };

    // constructors
    TermCriteria();
    // type can be MAX_ITER, EPS or MAX_ITER+EPS.
    // type = MAX_ITER means that only the number of iterations does matter;
    // type = EPS means that only the required precision (epsilon) does matter
    //    (though, most algorithms put some limit on the number of iterations anyway)
    // type = MAX_ITER + EPS means that algorithm stops when
    // either the specified number of iterations is made,
    // or when the specified accuracy is achieved - whatever happens first.
    TermCriteria(int _type, int _maxCount, double _epsilon);
    TermCriteria(const CvTermCriteria& criteria);
    operator CvTermCriteria() const;

    int type;
    int maxCount;
    double epsilon;
};

The class TermCriteria replaces the old CvTermCriteria and fully compatible with it.

Matx¶

Template class for small matrices

template<typename T, int m, int n> class Matx
{
public:
    typedef T value_type;
    enum { depth = DataDepth<T>::value, channels = m*n,
           type = CV_MAKETYPE(depth, channels) };

    // various methods
    ...

    Tp val[m*n];
};

typedef Matx<float, 1, 2> Matx12f;
typedef Matx<double, 1, 2> Matx12d;
...
typedef Matx<float, 1, 6> Matx16f;
typedef Matx<double, 1, 6> Matx16d;

typedef Matx<float, 2, 1> Matx21f;
typedef Matx<double, 2, 1> Matx21d;
...
typedef Matx<float, 6, 1> Matx61f;
typedef Matx<double, 6, 1> Matx61d;

typedef Matx<float, 2, 2> Matx22f;
typedef Matx<double, 2, 2> Matx22d;
...
typedef Matx<float, 6, 6> Matx66f;
typedef Matx<double, 6, 6> Matx66d;

The class represents small matrices, which type and size are known at compile time. If you need more flexible type, use Mat . The elements of a matrix M are accessible using M(i,j) notation, and most of the common matrix operations (see also MatrixExpressions ) are available. If you need to do some operation on Matx that is not implemented, it is easy to convert the matrix to Mat and backwards.

Matx33f m(1, 2, 3,
          4, 5, 6,
          7, 8, 9);
cout << sum(Mat(m*m.t())) << endl;

Vec¶

Template class for short numerical vectors

template<typename T, int cn> class Vec : public Matx<T, cn, 1>
{
public:
    typedef T value_type;
    enum { depth = DataDepth<T>::value, channels = cn,
           type = CV_MAKETYPE(depth, channels) };

    // various methods ...
};

typedef Vec<uchar, 2> Vec2b;
typedef Vec<uchar, 3> Vec3b;
typedef Vec<uchar, 4> Vec4b;

typedef Vec<short, 2> Vec2s;
typedef Vec<short, 3> Vec3s;
typedef Vec<short, 4> Vec4s;

typedef Vec<int, 2> Vec2i;
typedef Vec<int, 3> Vec3i;
typedef Vec<int, 4> Vec4i;

typedef Vec<float, 2> Vec2f;
typedef Vec<float, 3> Vec3f;
typedef Vec<float, 4> Vec4f;
typedef Vec<float, 6> Vec6f;

typedef Vec<double, 2> Vec2d;
typedef Vec<double, 3> Vec3d;
typedef Vec<double, 4> Vec4d;
typedef Vec<double, 6> Vec6d;

Vec is a partial case of Matx . It is possible to convert Vec<T,2> to/from Point_ , Vec<T,3> to/from Point3_ , and Vec<T,4> to CvScalar or Scalar . The elements of Vec are accessed using operator[] . All the expected vector operations are implemented too:

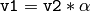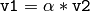$\texttt{v1} = \texttt{v2} \pm \texttt{v3}$ , $\texttt{v1} = \texttt{v2} * \alpha$ , $\texttt{v1} = \alpha * \texttt{v2}$ (plus the corresponding augmenting operations; note that these operations apply to the each computed vector component)
v1 == v2, v1 != v2
norm(v1) ( 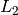$L_2$ -norm)

The class Vec is commonly used to describe pixel types of multi-channel arrays, see Mat_ description.

Scalar_¶

4-element vector

template<typename _Tp> class Scalar_ : public Vec<_Tp, 4>
{
public:
    Scalar_();
    Scalar_(_Tp v0, _Tp v1, _Tp v2=0, _Tp v3=0);
    Scalar_(const CvScalar& s);
    Scalar_(_Tp v0);
    static Scalar_<_Tp> all(_Tp v0);
    operator CvScalar() const;

    template<typename T2> operator Scalar_<T2>() const;

    Scalar_<_Tp> mul(const Scalar_<_Tp>& t, double scale=1 ) const;
    template<typename T2> void convertTo(T2* buf, int channels, int unroll_to=0) const;
};

typedef Scalar_<double> Scalar;

The template class Scalar_ and it’s double-precision instantiation Scalar represent 4-element vector. Being derived from Vec<_Tp, 4> , they can be used as typical 4-element vectors, but in addition they can be converted to/from CvScalar . The type Scalar is widely used in OpenCV for passing pixel values and it is a drop-in replacement for CvScalar that was used for the same purpose in the earlier versions of OpenCV.

Range¶

Specifies a continuous subsequence (a.k.a. slice) of a sequence.

class Range
{
public:
    Range();
    Range(int _start, int _end);
    Range(const CvSlice& slice);
    int size() const;
    bool empty() const;
    static Range all();
    operator CvSlice() const;

    int start, end;
};

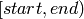The class is used to specify a row or column span in a matrix ( Mat ), and for many other purposes. Range(a,b) is basically the same as a:b in Matlab or a..b in Python. As in Python, start is inclusive left boundary of the range, and end is exclusive right boundary of the range. Such a half-opened interval is usually denoted as $[start,end)$ .

The static method Range::all() returns some special variable that means “the whole sequence” or “the whole range”, just like ” : ” in Matlab or ” ... ” in Python. All the methods and functions in OpenCV that take Range support this special Range::all() value, but of course, in the case of your own custom processing you will probably have to check and handle it explicitly:

void my_function(..., const Range& r, ....)
{
    if(r == Range::all()) {
        // process all the data
    }
    else {
        // process [r.start, r.end)
    }
}

Ptr¶

A template class for smart reference-counting pointers

template<typename _Tp> class Ptr
{
public:
    // default constructor
    Ptr();
    // constructor that wraps the object pointer
    Ptr(_Tp* _obj);
    // destructor: calls release()
    ~Ptr();
    // copy constructor; increments ptr's reference counter
    Ptr(const Ptr& ptr);
    // assignment operator; decrements own reference counter
    // (with release()) and increments ptr's reference counter
    Ptr& operator = (const Ptr& ptr);
    // increments reference counter
    void addref();
    // decrements reference counter; when it becomes 0,
    // delete_obj() is called
    void release();
    // user-specified custom object deletion operation.
    // by default, "delete obj;" is called
    void delete_obj();
    // returns true if obj == 0;
    bool empty() const;

    // provide access to the object fields and methods
    _Tp* operator -> ();
    const _Tp* operator -> () const;

    // return the underlying object pointer;
    // thanks to the methods, the Ptr<_Tp> can be
    // used instead of _Tp*
    operator _Tp* ();
    operator const _Tp*() const;
protected:
    // the encapsulated object pointer
    _Tp* obj;
    // the associated reference counter
    int* refcount;
};

The class Ptr<_Tp> is a template class that wraps pointers of the corresponding type. It is similar to shared_ptr that is a part of Boost library ( http://www.boost.org/doc/libs/1_40_0/libs/smart_ptr/shared_ptr.htm ) and also a part of the C++0x standard.

By using this class you can get the following capabilities:

default constructor, copy constructor and assignment operator for an arbitrary C++ class or a C structure. For some objects, like files, windows, mutexes, sockets etc, copy constructor or assignment operator are difficult to define. For some other objects, like complex classifiers in OpenCV, copy constructors are absent and not easy to implement. Finally, some of complex OpenCV and your own data structures may have been written in C. However, copy constructors and default constructors can simplify programming a lot; besides, they are often required (e.g. by STL containers). By wrapping a pointer to such a complex object TObj to Ptr<TObj> you will automatically get all of the necessary constructors and the assignment operator.
all the above-mentioned operations running very fast, regardless of the data size, i.e. as “O(1)” operations. Indeed, while some structures, like std::vector provide a copy constructor and an assignment operator, the operations may take considerable time if the data structures are big. But if the structures are put into Ptr<> , the overhead becomes small and independent of the data size.
automatic destruction, even for C structures. See the example below with FILE* .
heterogeneous collections of objects. The standard STL and most other C++ and OpenCV containers can only store objects of the same type and the same size. The classical solution to store objects of different types in the same container is to store pointers to the base class base_class_t* instead, but when you loose the automatic memory management. Again, by using Ptr<base_class_t>() instead of the raw pointers, you can solve the problem.

The class Ptr treats the wrapped object as a black box, the reference counter is allocated and managed separately. The only thing the pointer class needs to know about the object is how to deallocate it. This knowledge is incapsulated in Ptr::delete_obj() method, which is called when the reference counter becomes 0. If the object is a C++ class instance, no additional coding is needed, because the default implementation of this method calls delete obj; . However, if the object is deallocated in a different way, then the specialized method should be created. For example, if you want to wrap FILE , the delete_obj may be implemented as following:

template<> inline void Ptr<FILE>::delete_obj()
{
    fclose(obj); // no need to clear the pointer afterwards,
                 // it is done externally.
}
...

// now use it:
Ptr<FILE> f(fopen("myfile.txt", "r"));
if(f.empty())
    throw ...;
fprintf(f, ....);
...
// the file will be closed automatically by the Ptr<FILE> destructor.

Note : The reference increment/decrement operations are implemented as atomic operations, and therefore it is normally safe to use the classes in multi-threaded applications. The same is true for Mat and other C++ OpenCV classes that operate on the reference counters.

Mat¶

OpenCV C++ n-dimensional dense array class.

class CV_EXPORTS Mat
{
public:
    // ... a lot of methods ...
    ...

    /*! includes several bit-fields:
         - the magic signature
         - continuity flag
         - depth
         - number of channels
     */
    int flags;
    //! the array dimensionality, >= 2
    int dims;
    //! the number of rows and columns or (-1, -1) when the array has more than 2 dimensions
    int rows, cols;
    //! pointer to the data
    uchar* data;

    //! pointer to the reference counter;
    // when array points to user-allocated data, the pointer is NULL
    int* refcount;

    // other members
    ...
};

The class Mat represents an n-dimensional dense numerical single-channel or multi-channel array. It can be used to store real or complex-valued vectors and matrices, grayscale or color images, voxel volumes, vector fields, point clouds, tensors, histograms (though, very high-dimensional histograms may be better stored in a SparseMat ). 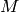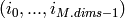The data layout of array $M$ is defined by the array M.step[] , so that the address of element $(i_0,...,i_{M.dims-1})$ , where $0\leq i_k<M.size[k]$ is computed as:

$addr(M_{i_0,...,i_{M.dims-1}}) = M.data + M.step[0]*i_0 + M.step[1]*i_1 + ... + M.step[M.dims-1]*i_{M.dims-1}$

In the case of 2-dimensional array the above formula is reduced to:

$addr(M_{i,j}) = M.data + M.step[0]*i + M.step[1]*j$

Note that M.step[i] >= M.step[i+1] (in fact, M.step[i] >= M.step[i+1]*M.size[i+1] ), that is, 2-dimensional matrices are stored row-by-row, 3-dimensional matrices are stored plane-by-plane etc. M.step[M.dims-1] is minimal and always equal to the element size M.elemSize() .

That is, the data layout in Mat is fully compatible with CvMat , IplImage and CvMatND types from OpenCV 1.x, as well as with majority of dense array types from the standard toolkits and SDKs, such as Numpy (ndarray), Win32 (independent device bitmaps) etc, i.e. any other array that uses “steps”, a.k.a. “strides”, to compute position of a pixel. Because of such compatibility, it is possible to make a Mat header for user-allocated data and process it in-place using OpenCV functions.

There are many different ways to create Mat object. Here are the some popular ones:

using create(nrows, ncols, type) method or

the similar constructor

Mat(nrows, ncols, type[, fillValue]) constructor.

A new array of the specified size and specifed type will be allocated.

type has the same meaning as in cvCreateMat() method,

e.g.

CV_8UC1 means 8-bit single-channel array,

CV_32FC2 means 2-channel (i.e. complex) floating-point array etc:
```
// make 7x7 complex matrix filled with 1+3j.
cv::Mat M(7,7,CV_32FC2,Scalar(1,3));
// and now turn M to 100x60 15-channel 8-bit matrix.
// The old content will be deallocated
M.create(100,60,CV_8UC(15));
```
As noted in the introduction of this chapter, create() will only allocate a new array when the current array shape

or type are different from the specified.
similarly to above, you can create a multi-dimensional array:
```
// create 100x100x100 8-bit array
int sz[] = {100, 100, 100};
cv::Mat bigCube(3, sz, CV_8U, Scalar::all(0));
```
note that it is pass number of dimensions =1 to the Mat constructor, but the created array will be 2-dimensional, with the number of columns set to 1. That’s why Mat::dims is always >= 2 (can also be 0 when the array is empty)
by using a copy constructor or assignment operator, where on the right side it can

be a array or expression, see below. Again, as noted in the introduction, array assignment is O(1) operation because it only copies the header and increases the reference counter.

Mat::clone() method can be used to get a full

(a.k.a. deep) copy of the array when you need it.

by constructing a header for a part of another array. It can be a single row, single column,: several rows, several columns, rectangular region in the array (called a minor in algebra) or a diagonal. Such operations are also O(1), because the new header will reference the same data. You can actually modify a part of the array using this feature, e.g.

// add 5-th row, multiplied by 3 to the 3rd row
M.row(3) = M.row(3) + M.row(5)*3;

// now copy 7-th column to the 1-st column
// M.col(1) = M.col(7); // this will not work
Mat M1 = M.col(1);
M.col(7).copyTo(M1);

// create new 320x240 image
cv::Mat img(Size(320,240),CV_8UC3);
// select a roi
cv::Mat roi(img, Rect(10,10,100,100));
// fill the ROI with (0,255,0) (which is green in RGB space);
// the original 320x240 image will be modified
roi = Scalar(0,255,0);

Thanks to the additional datastart and dataend members, it is possible to

compute the relative sub-array position in the main

“container” array using locateROI() :

Mat A = Mat::eye(10, 10, CV_32S);
// extracts A columns, 1 (inclusive) to 3 (exclusive).
Mat B = A(Range::all(), Range(1, 3));
// extracts B rows, 5 (inclusive) to 9 (exclusive).
// that is, C ~ A(Range(5, 9), Range(1, 3))
Mat C = B(Range(5, 9), Range::all());
Size size; Point ofs;
C.locateROI(size, ofs);
// size will be (width=10,height=10) and the ofs will be (x=1, y=5)

As in the case of whole matrices, if you need a deep copy, use clone() method

of the extracted sub-matrices.

by making a header for user-allocated-data. It can be useful for

processing “foreign” data using OpenCV (e.g. when you implement: a DirectShow filter or a processing module for gstreamer etc.), e.g.

void process_video_frame(const unsigned char* pixels,
                         int width, int height, int step)
{
    cv::Mat img(height, width, CV_8UC3, pixels, step);
    cv::GaussianBlur(img, img, cv::Size(7,7), 1.5, 1.5);
}

for quick initialization of small matrices and/or super-fast element access

double m[3][3] = {{a, b, c}, {d, e, f}, {g, h, i}};
cv::Mat M = cv::Mat(3, 3, CV_64F, m).inv();

partial yet very common cases of this “user-allocated data” case are conversions: from

CvMat and IplImage to Mat . For this purpose there are special constructors

taking pointers to

CvMat or IplImage and the optional

flag indicating whether to copy the data or not.

Backward conversion from

Mat to CvMat or IplImage is provided via cast operators

Mat::operator CvMat() const an Mat::operator IplImage() .

The operators do

not copy the data.

IplImage* img = cvLoadImage("greatwave.jpg", 1);
Mat mtx(img); // convert IplImage* -> cv::Mat
CvMat oldmat = mtx; // convert cv::Mat -> CvMat
CV_Assert(oldmat.cols == img->width && oldmat.rows == img->height &&
    oldmat.data.ptr == (uchar*)img->imageData && oldmat.step == img->widthStep);

by using MATLAB-style array initializers, zeros(), ones(), eye() , e.g.:

// create a double-precision identity martix and add it to M.
M += Mat::eye(M.rows, M.cols, CV_64F);

by using comma-separated initializer:
```
// create 3x3 double-precision identity matrix
Mat M = (Mat_<double>(3,3) << 1, 0, 0, 0, 1, 0, 0, 0, 1);
```
here we first call constructor of Mat_ class (that we describe further) with the proper parameters, and then we just put << operator followed by comma-separated values that can be constants, variables, expressions etc. Also, note the extra parentheses that are needed to avoid compiler errors.

Once array is created, it will be automatically managed by using reference-counting mechanism (unless the array header is built on top of user-allocated data, in which case you should handle the data by yourself). The array data will be deallocated when no one points to it; if you want to release the data pointed by a array header before the array destructor is called, use Mat::release() .

The next important thing to learn about the array class is element access. Earlier it was shown how to compute address of each array element. Normally, it’s not needed to use the formula directly in your code. If you know the array element type (which can be retrieved using the method Mat::type() ), you can access element 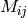$M_{ij}$ of 2-dimensional array as:

M.at<double>(i,j) += 1.f;

assuming that M is double-precision floating-point array. There are several variants of the method at for different number of dimensions.

If you need to process a whole row of a 2d array, the most efficient way is to get the pointer to the row first, and then just use plain C operator [] :

// compute sum of positive matrix elements
// (assuming that M is double-precision matrix)
double sum=0;
for(int i = 0; i < M.rows; i++)
{
    const double* Mi = M.ptr<double>(i);
    for(int j = 0; j < M.cols; j++)
        sum += std::max(Mi[j], 0.);
}

Some operations, like the above one, do not actually depend on the array shape, they just process elements of an array one by one (or elements from multiple arrays that have the same coordinates, e.g. array addition). Such operations are called element-wise and it makes sense to check whether all the input/output arrays are continuous, i.e. have no gaps in the end of each row, and if yes, process them as a single long row:

// compute sum of positive matrix elements, optimized variant
double sum=0;
int cols = M.cols, rows = M.rows;
if(M.isContinuous())
{
    cols *= rows;
    rows = 1;
}
for(int i = 0; i < rows; i++)
{
    const double* Mi = M.ptr<double>(i);
    for(int j = 0; j < cols; j++)
        sum += std::max(Mi[j], 0.);
}

in the case of continuous matrix the outer loop body will be executed just once, so the overhead will be smaller, which will be especially noticeable in the case of small matrices.

Finally, there are STL-style iterators that are smart enough to skip gaps between successive rows:

// compute sum of positive matrix elements, iterator-based variant
double sum=0;
MatConstIterator_<double> it = M.begin<double>(), it_end = M.end<double>();
for(; it != it_end; ++it)
    sum += std::max(*it, 0.);

The matrix iterators are random-access iterators, so they can be passed to any STL algorithm, including std::sort() .

Matrix Expressions¶

This is a list of implemented matrix operations that can be combined in arbitrary complex expressions (here A , B stand for matrices ( Mat ), s for a scalar ( Scalar ), 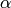$\alpha$ for a real-valued scalar ( double )):

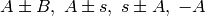
addition, subtraction, negation: $A \pm B,\;A \pm s,\;s \pm A,\;-A$
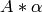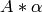
scaling: $A*\alpha$ , $A*\alpha$
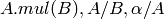
per-element multiplication and division: $A.mul(B), A/B, \alpha/A$
matrix multiplication: $A*B$
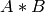
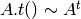
transposition: $A.t() \sim A^t$
matrix inversion and pseudo-inversion, solving linear systems and least-squares problems:

$A.inv([method]) \sim A^{-1}, A.inv([method])*B \sim X:\,AX=B$
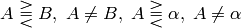comparison: $A\gtreqqless B,\;A \ne B,\;A \gtreqqless \alpha,\;A \ne \alpha$ .

The result of comparison is 8-bit single channel mask, which elements are set to 255 (if the particular element or pair of elements satisfy the condition) and 0 otherwise.
bitwise logical operations: A & B, A & s, A | B, A | s, A textasciicircum B, A textasciicircum s, ~ A
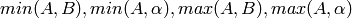
element-wise minimum and maximum: $min(A, B), min(A, \alpha), max(A, B), max(A, \alpha)$
element-wise absolute value: $abs(A)$
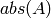
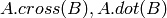
cross-product, dot-product: $A.cross(B), A.dot(B)$
any function of matrix or matrices and scalars that returns a matrix or a scalar, such as

norm() , mean() , sum() , countNonZero() , trace() ,

determinant() , repeat() etc.
matrix initializers ( eye(), zeros(), ones() ), matrix comma-separated initializers,

matrix constructors and operators that extract sub-matrices (see

Mat description).
verb “Mat_<destination_type>()” constructors to cast the result to the proper type.

Note, however, that comma-separated initializers and probably some other operations may require additional explicit Mat() or verb “Mat_<T>()” constuctor calls to resolve possible ambiguity.

Below is the formal description of the Mat methods.

Navigation

Basic Structures¶

DataType¶

Point_¶

Point3_¶

Size_¶

Rect_¶

RotatedRect¶

TermCriteria¶

Matx¶

Vec¶

Scalar_¶

Range¶

Ptr¶

Mat¶

Matrix Expressions¶

cv::Mat::Mat¶

cv::Mat::Mat¶

cv::Mat::operator =¶

cv::Mat::operator MatExpr¶

cv::Mat::row¶

cv::Mat::col¶

cv::Mat::rowRange¶

cv::Mat::colRange¶

cv::Mat::diag¶

cv::Mat::clone¶

cv::Mat::copyTo¶

cv::Mat::convertTo¶

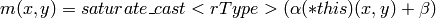
cv::Mat::assignTo¶

cv::Mat::setTo¶

cv::Mat::reshape¶

cv::Mat::t¶

cv::Mat::inv¶

cv::Mat::mul¶

cv::Mat::cross¶

cv::Mat::dot¶

cv::Mat::zeros¶

cv::Mat::ones¶

cv::Mat::eye¶

cv::Mat::create¶

cv::Mat::addref¶

cv::Mat::release¶

cv::Mat::resize¶

Mat::push_back¶

Mat::pop_back¶

cv::Mat::locateROI¶

cv::Mat::adjustROI¶

cv::Mat::operator()¶

cv::Mat::operator CvMat¶

cv::Mat::operator IplImage¶

cv::Mat::total¶

cv::Mat::isContinuous¶

cv::Mat::elemSize¶

cv::Mat::elemSize1¶

cv::Mat::type¶

cv::Mat::depth¶

cv::Mat::channels¶

cv::Mat::step1¶

cv::Mat::size¶

cv::Mat::empty¶

cv::Mat::ptr¶

cv::Mat::at¶

cv::Mat::begin¶

cv::Mat::end¶

Mat_¶

NAryMatIterator¶

SparseMat¶

SparseMat_¶

Help and Feedback

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Navigation