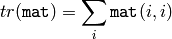Operations on Arrays¶
AbsDiff¶
- AbsDiff(src1, src2, dst) → None¶
Calculates absolute difference between two arrays.
Parameters:
The function calculates absolute difference between two arrays.
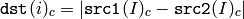
All the arrays must have the same data type and the same size (or ROI size).
AbsDiffS¶
- AbsDiffS(src, value, dst) → None¶
Calculates absolute difference between an array and a scalar.
Parameters:
The function calculates absolute difference between an array and a scalar.
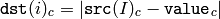
All the arrays must have the same data type and the same size (or ROI size).
Add¶
- Add(src1, src2, dst, mask=NULL) → None¶
Computes the per-element sum of two arrays.
Parameters:
The function adds one array to another:
dst(I)=src1(I)+src2(I) if mask(I)!=0
All the arrays must have the same type, except the mask, and the same size (or ROI size). For types that have limited range this operation is saturating.
AddS¶
- AddS(src, value, dst, mask=NULL) → None¶
Computes the sum of an array and a scalar.
Parameters:
The function adds a scalar value to every element in the source array src1 and stores the result in dst . For types that have limited range this operation is saturating.
dst(I)=src(I)+value if mask(I)!=0
All the arrays must have the same type, except the mask, and the same size (or ROI size).
AddWeighted¶
- AddWeighted(src1, alpha, src2, beta, gamma, dst) → None¶
Computes the weighted sum of two arrays.
Parameters:
The function calculates the weighted sum of two arrays as follows:
dst(I)=src1(I)*alpha+src2(I)*beta+gamma
All the arrays must have the same type and the same size (or ROI size). For types that have limited range this operation is saturating.
And¶
- And(src1, src2, dst, mask=NULL) → None¶
Calculates per-element bit-wise conjunction of two arrays.
Parameters:
The function calculates per-element bit-wise logical conjunction of two arrays:
dst(I)=src1(I)&src2(I) if mask(I)!=0
In the case of floating-point arrays their bit representations are used for the operation. All the arrays must have the same type, except the mask, and the same size.
AndS¶
- AndS(src, value, dst, mask=NULL) → None¶
Calculates per-element bit-wise conjunction of an array and a scalar.
Parameters:
The function calculates per-element bit-wise conjunction of an array and a scalar:
dst(I)=src(I)&value if mask(I)!=0
Prior to the actual operation, the scalar is converted to the same type as that of the array(s). In the case of floating-point arrays their bit representations are used for the operation. All the arrays must have the same type, except the mask, and the same size.
Avg¶
- Avg(arr, mask=NULL) → CvScalar¶
Calculates average (mean) of array elements.
Parameters:
The function calculates the average value M of array elements, independently for each channel:
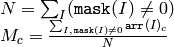
If the array is
IplImage
and COI is set, the function processes the selected channel only and stores the average to the first scalar component
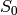 .
.
AvgSdv¶
- AvgSdv(arr, mask=NULL)-> (mean, stdDev)¶
Calculates average (mean) of array elements.
Parameters:
The function calculates the average value and standard deviation of array elements, independently for each channel:
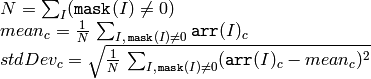
If the array is
IplImage
and COI is set, the function processes the selected channel only and stores the average and standard deviation to the first components of the output scalars (
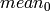 and
and
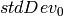 ).
).
CalcCovarMatrix¶
- CalcCovarMatrix(vects, covMat, avg, flags) → None¶
Calculates covariance matrix of a set of vectors.
Parameters: - vects (cvarr_count) – The input vectors, all of which must have the same type and the same size. The vectors do not have to be 1D, they can be 2D (e.g., images) and so forth
- covMat (CvArr) – The output covariance matrix that should be floating-point and square
- avg (CvArr) – The input or output (depending on the flags) array - the mean (average) vector of the input vectors
- flags (int) –
The operation flags, a combination of the following values
- CV_COVAR_SCRAMBLED The output covariance matrix is calculated as:
![\texttt{scale} * [ \texttt{vects} [0]- \texttt{avg} , \texttt{vects} [1]- \texttt{avg} ,...]^T \cdot [ \texttt{vects} [0]- \texttt{avg} , \texttt{vects} [1]- \texttt{avg} ,...]](_images/math/7f121e9a7fbd907244db1f391264bd164b6cdc17.png)
, that is, the covariance matrix is
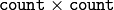 .
Such an unusual covariance matrix is used for fast PCA
of a set of very large vectors (see, for example, the EigenFaces technique
for face recognition). Eigenvalues of this “scrambled” matrix will
match the eigenvalues of the true covariance matrix and the “true”
eigenvectors can be easily calculated from the eigenvectors of the
“scrambled” covariance matrix.
.
Such an unusual covariance matrix is used for fast PCA
of a set of very large vectors (see, for example, the EigenFaces technique
for face recognition). Eigenvalues of this “scrambled” matrix will
match the eigenvalues of the true covariance matrix and the “true”
eigenvectors can be easily calculated from the eigenvectors of the
“scrambled” covariance matrix. - CV_COVAR_NORMAL The output covariance matrix is calculated as:
![\texttt{scale} * [ \texttt{vects} [0]- \texttt{avg} , \texttt{vects} [1]- \texttt{avg} ,...] \cdot [ \texttt{vects} [0]- \texttt{avg} , \texttt{vects} [1]- \texttt{avg} ,...]^T](_images/math/1aec123e6259450ead5046e17ac22e49cddce623.png)
, that is, covMat will be a covariance matrix with the same linear size as the total number of elements in each input vector. One and only one of CV_COVAR_SCRAMBLED and CV_COVAR_NORMAL must be specified
- CV_COVAR_USE_AVG If the flag is specified, the function does not calculate avg from the input vectors, but, instead, uses the passed avg vector. This is useful if avg has been already calculated somehow, or if the covariance matrix is calculated by parts - in this case, avg is not a mean vector of the input sub-set of vectors, but rather the mean vector of the whole set.
- CV_COVAR_SCALE If the flag is specified, the covariance matrix is scaled. In the “normal” mode scale is ‘1./count’; in the “scrambled” mode scale is the reciprocal of the total number of elements in each input vector. By default (if the flag is not specified) the covariance matrix is not scaled (‘scale=1’).
- CV_COVAR_ROWS Means that all the input vectors are stored as rows of a single matrix, vects[0] . count is ignored in this case, and avg should be a single-row vector of an appropriate size.
- CV_COVAR_COLS Means that all the input vectors are stored as columns of a single matrix, vects[0] . count is ignored in this case, and avg should be a single-column vector of an appropriate size.
- CV_COVAR_SCRAMBLED The output covariance matrix is calculated as:
The function calculates the covariance matrix and, optionally, the mean vector of the set of input vectors. The function can be used for PCA, for comparing vectors using Mahalanobis distance and so forth.
CartToPolar¶
- CartToPolar(x, y, magnitude, angle=NULL, angleInDegrees=0) → None¶
Calculates the magnitude and/or angle of 2d vectors.
Parameters: - x (CvArr) – The array of x-coordinates
- y (CvArr) – The array of y-coordinates
- magnitude (CvArr) – The destination array of magnitudes, may be set to NULL if it is not needed
- angle (CvArr) – The destination array of angles, may be set to NULL if it is not needed. The angles are measured in radians
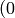 to
to 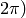 or in degrees (0 to 360 degrees).
or in degrees (0 to 360 degrees). - angleInDegrees (int) – The flag indicating whether the angles are measured in radians, which is default mode, or in degrees
The function calculates either the magnitude, angle, or both of every 2d vector (x(I),y(I)):
magnitude(I)=sqrt(x(I)^2^+y(I)^2^ ),
angle(I)=atan(y(I)/x(I) )
The angles are calculated with 0.1 degree accuracy. For the (0,0) point, the angle is set to 0.
Cbrt¶
- Cbrt(value) → float¶
Calculates the cubic root
Parameters: value (float) – The input floating-point value
The function calculates the cubic root of the argument, and normally it is faster than
pow(value,1./3)
. In addition, negative arguments are handled properly. Special values (
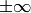 , NaN) are not handled.
, NaN) are not handled.
ClearND¶
- ClearND(arr, idx) → None¶
Clears a specific array element.
Parameters: - arr (CvArr) – Input array
- idx (sequence of int) – Array of the element indices
The function ClearND clears (sets to zero) a specific element of a dense array or deletes the element of a sparse array. If the sparse array element does not exists, the function does nothing.
CloneImage¶
- CloneImage(image) → copy¶
Makes a full copy of an image, including the header, data, and ROI.
Parameters: image (IplImage) – The original image
The returned IplImage* points to the image copy.
CloneMat¶
Creates a full copy of a matrix and returns a pointer to the copy.
CloneMatND¶
Cmp¶
- Cmp(src1, src2, dst, cmpOp) → None¶
Performs per-element comparison of two arrays.
Parameters: - src1 (CvArr) – The first source array
- src2 (CvArr) – The second source array. Both source arrays must have a single channel.
- dst (CvArr) – The destination array, must have 8u or 8s type
- cmpOp (int) –
The flag specifying the relation between the elements to be checked
- CV_CMP_EQ src1(I) “equal to” value
- CV_CMP_GT src1(I) “greater than” value
- CV_CMP_GE src1(I) “greater or equal” value
- CV_CMP_LT src1(I) “less than” value
- CV_CMP_LE src1(I) “less or equal” value
- CV_CMP_NE src1(I) “not equal” value
The function compares the corresponding elements of two arrays and fills the destination mask array:
dst(I)=src1(I) op src2(I),
dst(I) is set to 0xff (all 1 -bits) if the specific relation between the elements is true and 0 otherwise. All the arrays must have the same type, except the destination, and the same size (or ROI size)
CmpS¶
- CmpS(src, value, dst, cmpOp) → None¶
Performs per-element comparison of an array and a scalar.
Parameters: - src (CvArr) – The source array, must have a single channel
- value (float) – The scalar value to compare each array element with
- dst (CvArr) – The destination array, must have 8u or 8s type
- cmpOp (int) –
The flag specifying the relation between the elements to be checked
- CV_CMP_EQ src1(I) “equal to” value
- CV_CMP_GT src1(I) “greater than” value
- CV_CMP_GE src1(I) “greater or equal” value
- CV_CMP_LT src1(I) “less than” value
- CV_CMP_LE src1(I) “less or equal” value
- CV_CMP_NE src1(I) “not equal” value
The function compares the corresponding elements of an array and a scalar and fills the destination mask array:
dst(I)=src(I) op scalar
where
op
is
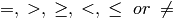 .
.
dst(I) is set to 0xff (all 1 -bits) if the specific relation between the elements is true and 0 otherwise. All the arrays must have the same size (or ROI size).
Convert¶
- Convert(src, dst) → None¶
Converts one array to another.
Parameters:
The type of conversion is done with rounding and saturation, that is if the result of scaling + conversion can not be represented exactly by a value of the destination array element type, it is set to the nearest representable value on the real axis.
All the channels of multi-channel arrays are processed independently.
ConvertScale¶
- ConvertScale(src, dst, scale=1.0, shift=0.0) → None¶
Converts one array to another with optional linear transformation.
Parameters:
The function has several different purposes, and thus has several different names. It copies one array to another with optional scaling, which is performed first, and/or optional type conversion, performed after:
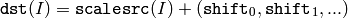
All the channels of multi-channel arrays are processed independently.
The type of conversion is done with rounding and saturation, that is if the result of scaling + conversion can not be represented exactly by a value of the destination array element type, it is set to the nearest representable value on the real axis.
In the case of scale=1, shift=0 no prescaling is done. This is a specially optimized case and it has the appropriate Convert name. If source and destination array types have equal types, this is also a special case that can be used to scale and shift a matrix or an image and that is caled Scale .
ConvertScaleAbs¶
- ConvertScaleAbs(src, dst, scale=1.0, shift=0.0) → None¶
Converts input array elements to another 8-bit unsigned integer with optional linear transformation.
Parameters:
The function is similar to ConvertScale , but it stores absolute values of the conversion results:
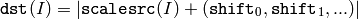
The function supports only destination arrays of 8u (8-bit unsigned integers) type; for other types the function can be emulated by a combination of ConvertScale and Abs functions.
CvtScaleAbs¶
- CvtScaleAbs(src, dst, scale=1.0, shift=0.0) → None¶
Converts input array elements to another 8-bit unsigned integer with optional linear transformation.
Parameters: - src – Source array
- dst – Destination array (should have 8u depth)
- scale – ScaleAbs factor
- shift – Value added to the scaled source array elements
The function is similar to ConvertScale , but it stores absolute values of the conversion results:
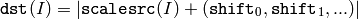
The function supports only destination arrays of 8u (8-bit unsigned integers) type; for other types the function can be emulated by a combination of ConvertScale and Abs functions.
Copy¶
- Copy(src, dst, mask=NULL) → None¶
Copies one array to another.
Parameters:
The function copies selected elements from an input array to an output array:

If any of the passed arrays is of IplImage type, then its ROI and COI fields are used. Both arrays must have the same type, the same number of dimensions, and the same size. The function can also copy sparse arrays (mask is not supported in this case).
CountNonZero¶
- CountNonZero(arr) → int¶
Counts non-zero array elements.
Parameters: arr (CvArr) – The array must be a single-channel array or a multi-channel image with COI set
The function returns the number of non-zero elements in arr:
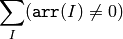
In the case of IplImage both ROI and COI are supported.
CreateData¶
The function allocates image, matrix or multi-dimensional array data. Note that in the case of matrix types OpenCV allocation functions are used and in the case of IplImage they are used unless CV_TURN_ON_IPL_COMPATIBILITY was called. In the latter case IPL functions are used to allocate the data.
CreateImage¶
- CreateImage(size, depth, channels) → image¶
Creates an image header and allocates the image data.
Parameters:
CreateImageHeader¶
- CreateImageHeader(size, depth, channels) → image¶
Creates an image header but does not allocate the image data.
Parameters: - size (CvSize) – Image width and height
- depth (int) – Image depth (see CreateImage )
- channels (int) – Number of channels (see CreateImage )
CreateMat¶
- CreateMat(rows, cols, type) → mat¶
Creates a matrix header and allocates the matrix data.
Parameters: - rows (int) – Number of rows in the matrix
- cols (int) – Number of columns in the matrix
- type (int) – The type of the matrix elements in the form CV_<bit depth><S|U|F>C<number of channels> , where S=signed, U=unsigned, F=float. For example, CV _ 8UC1 means the elements are 8-bit unsigned and the there is 1 channel, and CV _ 32SC2 means the elements are 32-bit signed and there are 2 channels.
CreateMatHeader¶
- CreateMatHeader(rows, cols, type) → mat¶
Creates a matrix header but does not allocate the matrix data.
Parameters: - rows (int) – Number of rows in the matrix
- cols (int) – Number of columns in the matrix
- type (int) – Type of the matrix elements, see CreateMat
The function allocates a new matrix header and returns a pointer to it. The matrix data can then be allocated using CreateData or set explicitly to user-allocated data via SetData .
CreateMatND¶
- CreateMatND(dims, type) → None¶
Creates the header and allocates the data for a multi-dimensional dense array.
Parameters: - dims (sequence of int) – List or tuple of array dimensions, up to 32 in length.
- type (int) – Type of array elements, see CreateMat .
This is a short form for:
CreateMatNDHeader¶
- CreateMatNDHeader(dims, type) → None¶
Creates a new matrix header but does not allocate the matrix data.
Parameters: - dims (sequence of int) – List or tuple of array dimensions, up to 32 in length.
- type (int) – Type of array elements, see CreateMat
The function allocates a header for a multi-dimensional dense array. The array data can further be allocated using CreateData or set explicitly to user-allocated data via SetData .
CrossProduct¶
- CrossProduct(src1, src2, dst) → None¶
Calculates the cross product of two 3D vectors.
Parameters:
The function calculates the cross product of two 3D vectors:
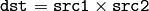
or:
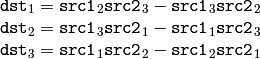
DCT¶
- DCT(src, dst, flags) → None¶
Performs a forward or inverse Discrete Cosine transform of a 1D or 2D floating-point array.
Parameters: - src (CvArr) – Source array, real 1D or 2D array
- dst (CvArr) – Destination array of the same size and same type as the source
- flags (int) –
Transformation flags, a combination of the following values
- CV_DXT_FORWARD do a forward 1D or 2D transform.
- CV_DXT_INVERSE do an inverse 1D or 2D transform.
- CV_DXT_ROWS do a forward or inverse transform of every individual row of the input matrix. This flag allows user to transform multiple vectors simultaneously and can be used to decrease the overhead (which is sometimes several times larger than the processing itself), to do 3D and higher-dimensional transforms and so forth.
The function performs a forward or inverse transform of a 1D or 2D floating-point array:
Forward Cosine transform of 1D vector of
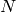 elements:
elements:
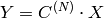
where
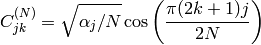
and
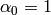 ,
,
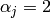 for
for
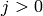 .
.
Inverse Cosine transform of 1D vector of N elements:
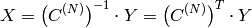
(since
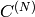 is orthogonal matrix,
is orthogonal matrix,
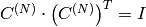 )
)
Forward Cosine transform of 2D
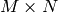 matrix:
matrix:
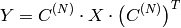
Inverse Cosine transform of 2D vector of
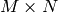 elements:
elements:
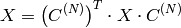
DFT¶
- DFT(src, dst, flags, nonzeroRows=0) → None¶
Performs a forward or inverse Discrete Fourier transform of a 1D or 2D floating-point array.
Parameters: - src (CvArr) – Source array, real or complex
- dst (CvArr) – Destination array of the same size and same type as the source
- flags (int) –
Transformation flags, a combination of the following values
- CV_DXT_FORWARD do a forward 1D or 2D transform. The result is not scaled.
- CV_DXT_INVERSE do an inverse 1D or 2D transform. The result is not scaled. CV_DXT_FORWARD and CV_DXT_INVERSE are mutually exclusive, of course.
- CV_DXT_SCALE scale the result: divide it by the number of array elements. Usually, it is combined with CV_DXT_INVERSE , and one may use a shortcut CV_DXT_INV_SCALE .
- CV_DXT_ROWS do a forward or inverse transform of every individual row of the input matrix. This flag allows the user to transform multiple vectors simultaneously and can be used to decrease the overhead (which is sometimes several times larger than the processing itself), to do 3D and higher-dimensional transforms and so forth.
- CV_DXT_INVERSE_SCALE same as CV_DXT_INVERSE + CV_DXT_SCALE
- nonzeroRows (int) – Number of nonzero rows in the source array (in the case of a forward 2d transform), or a number of rows of interest in the destination array (in the case of an inverse 2d transform). If the value is negative, zero, or greater than the total number of rows, it is ignored. The parameter can be used to speed up 2d convolution/correlation when computing via DFT. See the example below.
The function performs a forward or inverse transform of a 1D or 2D floating-point array:
Forward Fourier transform of 1D vector of N elements:
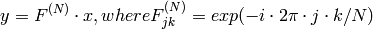
,
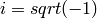
Inverse Fourier transform of 1D vector of N elements:
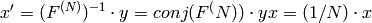
Forward Fourier transform of 2D vector of M
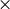 N elements:
N elements:
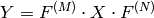
Inverse Fourier transform of 2D vector of M
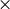 N elements:
N elements:
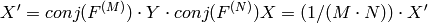
In the case of real (single-channel) data, the packed format, borrowed from IPL, is used to represent the result of a forward Fourier transform or input for an inverse Fourier transform:
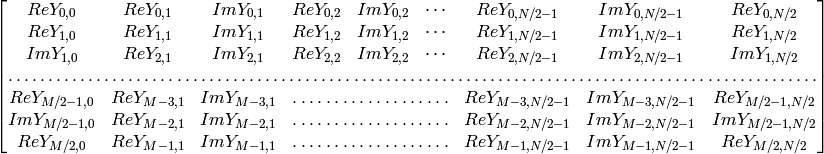
Note: the last column is present if N is even, the last row is present if M is even. In the case of 1D real transform the result looks like the first row of the above matrix.
Here is the example of how to compute 2D convolution using DFT.
Det¶
The function returns the determinant of the square matrix
mat
. The direct method is used for small matrices and Gaussian elimination is used for larger matrices. For symmetric positive-determined matrices, it is also possible to run
SVD
with
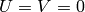 and then calculate the determinant as a product of the diagonal elements of
and then calculate the determinant as a product of the diagonal elements of
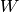 .
.
Div¶
- Div(src1, src2, dst, scale) → None¶
Performs per-element division of two arrays.
Parameters:
The function divides one array by another:
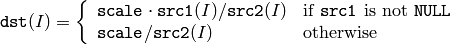
All the arrays must have the same type and the same size (or ROI size).
DotProduct¶
- DotProduct(src1, src2) → double¶
Calculates the dot product of two arrays in Euclidian metrics.
Parameters:
The function calculates and returns the Euclidean dot product of two arrays.
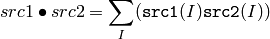
In the case of multiple channel arrays, the results for all channels are accumulated. In particular,
cvDotProduct(a,a)
where
a
is a complex vector, will return
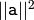 .
The function can process multi-dimensional arrays, row by row, layer by layer, and so on.
.
The function can process multi-dimensional arrays, row by row, layer by layer, and so on.
EigenVV¶
- EigenVV(mat, evects, evals, eps, lowindex, highindex) → None¶
Computes eigenvalues and eigenvectors of a symmetric matrix.
Parameters: - mat (CvArr) – The input symmetric square matrix, modified during the processing
- evects (CvArr) – The output matrix of eigenvectors, stored as subsequent rows
- evals (CvArr) – The output vector of eigenvalues, stored in the descending order (order of eigenvalues and eigenvectors is syncronized, of course)
- eps (float) – Accuracy of diagonalization. Typically, DBL_EPSILON (about
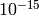 ) works well.
THIS PARAMETER IS CURRENTLY IGNORED.
) works well.
THIS PARAMETER IS CURRENTLY IGNORED. - lowindex (int) – Optional index of largest eigenvalue/-vector to calculate. (See below.)
- highindex (int) – Optional index of smallest eigenvalue/-vector to calculate. (See below.)
The function computes the eigenvalues and eigenvectors of matrix A :
mat*evects(i,:)' = evals(i)*evects(i,:)' (in MATLAB notation)
If either low- or highindex is supplied the other is required, too. Indexing is 0-based. Example: To calculate the largest eigenvector/-value set lowindex=highindex=0 . To calculate all the eigenvalues, leave lowindex=highindex=-1 . For legacy reasons this function always returns a square matrix the same size as the source matrix with eigenvectors and a vector the length of the source matrix with eigenvalues. The selected eigenvectors/-values are always in the first highindex - lowindex + 1 rows.
The contents of matrix A is destroyed by the function.
Currently the function is slower than SVD yet less accurate, so if A is known to be positively-defined (for example, it is a covariance matrix)it is recommended to use SVD to find eigenvalues and eigenvectors of A , especially if eigenvectors are not required.
Exp¶
- Exp(src, dst) → None¶
Calculates the exponent of every array element.
Parameters:
The function calculates the exponent of every element of the input array:
![\texttt{dst} [I] = e^{ \texttt{src} (I)}](_images/math/496d2ddec2bb134c04e7cc31b2f20a5023d602e7.png)
The maximum relative error is about
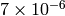 . Currently, the function converts denormalized values to zeros on output.
. Currently, the function converts denormalized values to zeros on output.
FastArctan¶
- FastArctan(y, x) → float¶
Calculates the angle of a 2D vector.
Parameters: - x (float) – x-coordinate of 2D vector
- y (float) – y-coordinate of 2D vector
The function calculates the full-range angle of an input 2D vector. The angle is measured in degrees and varies from 0 degrees to 360 degrees. The accuracy is about 0.1 degrees.
Flip¶
- Flip(src, dst=NULL, flipMode=0) → None¶
Flip a 2D array around vertical, horizontal or both axes.
Parameters: - src (CvArr) – Source array
- dst (CvArr) – Destination array.
If
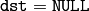 the flipping is done in place.
the flipping is done in place. - flipMode (int) – Specifies how to flip the array: 0 means flipping around the x-axis, positive (e.g., 1) means flipping around y-axis, and negative (e.g., -1) means flipping around both axes. See also the discussion below for the formulas:
The function flips the array in one of three different ways (row and column indices are 0-based):
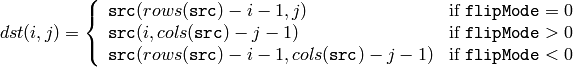
The example scenarios of function use are:
- vertical flipping of the image (flipMode = 0) to switch between top-left and bottom-left image origin, which is a typical operation in video processing under Win32 systems.
- horizontal flipping of the image with subsequent horizontal shift and absolute difference calculation to check for a vertical-axis symmetry (flipMode
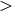 0)
0) - simultaneous horizontal and vertical flipping of the image with subsequent shift and absolute difference calculation to check for a central symmetry (flipMode
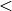 0)
0) - reversing the order of 1d point arrays (flipMode > 0)
fromarray¶
- fromarray(object, allowND = False) → CvMat
Create a CvMat from an object that supports the array interface.
Parameters: - object – Any object that supports the array interface
- allowND – If true, will return a CvMatND
If the object supports the array interface , return a CvMat ( allowND = False ) or CvMatND ( allowND = True ).
If allowND = False , then the object’s array must be either 2D or 3D. If it is 2D, then the returned CvMat has a single channel. If it is 3D, then the returned CvMat will have N channels, where N is the last dimension of the array. In this case, N cannot be greater than OpenCV’s channel limit, CV_CN_MAX .
If allowND = True , then fromarray returns a single-channel CvMatND with the same shape as the original array.
For example, NumPy arrays support the array interface, so can be converted to OpenCV objects:
>>> import cv, numpy
>>> a = numpy.ones((480, 640))
>>> mat = cv.fromarray(a)
>>> print cv.GetDims(mat), cv.CV_MAT_CN(cv.GetElemType(mat))
(480, 640) 1
>>> a = numpy.ones((480, 640, 3))
>>> mat = cv.fromarray(a)
>>> print cv.GetDims(mat), cv.CV_MAT_CN(cv.GetElemType(mat))
(480, 640) 3
>>> a = numpy.ones((480, 640, 3))
>>> mat = cv.fromarray(a, allowND = True)
>>> print cv.GetDims(mat), cv.CV_MAT_CN(cv.GetElemType(mat))
(480, 640, 3) 1
GEMM¶
- GEMM(src1, src2, alphs, src3, beta, dst, tABC=0) → None¶
Performs generalized matrix multiplication.
Parameters: - src1 (CvArr) – The first source array
- src2 (CvArr) – The second source array
- src3 (CvArr) – The third source array (shift). Can be NULL, if there is no shift.
- dst (CvArr) – The destination array
- tABC (int) –
The operation flags that can be 0 or a combination of the following values
- CV_GEMM_A_T transpose src1
- CV_GEMM_B_T transpose src2
- CV_GEMM_C_T transpose src3
For example, CV_GEMM_A_T+CV_GEMM_C_T corresponds to
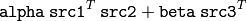
The function performs generalized matrix multiplication:

All the matrices should have the same data type and coordinated sizes. Real or complex floating-point matrices are supported.
Get1D¶
- Get1D(arr, idx) → scalar¶
Return a specific array element.
Parameters: - arr (CvArr) – Input array
- idx (int) – Zero-based element index
Return a specific array element. Array must have dimension 3.
Get2D¶
- Get2D(arr, idx0, idx1) → scalar¶
Return a specific array element.
Parameters: - arr (CvArr) – Input array
- idx0 (int) – Zero-based element row index
- idx1 (int) – Zero-based element column index
Return a specific array element. Array must have dimension 2.
Get3D¶
- Get3D(arr, idx0, idx1, idx2) → scalar¶
Return a specific array element.
Parameters: - arr (CvArr) – Input array
- idx0 (int) – Zero-based element index
- idx1 (int) – Zero-based element index
- idx2 (int) – Zero-based element index
Return a specific array element. Array must have dimension 3.
GetND¶
- GetND(arr, indices) → scalar¶
Return a specific array element.
Parameters: - arr (CvArr) – Input array
- indices (sequence of int) – List of zero-based element indices
Return a specific array element. The length of array indices must be the same as the dimension of the array.
GetCol¶
- GetCol(arr, col) → submat¶
Returns array column.
Parameters:
The function GetCol returns a single column from the input array.
GetCols¶
- GetCols(arr, startCol, endCol) → submat¶
Returns array column span.
Parameters:
The function GetCols returns a column span from the input array.
GetDiag¶
- GetDiag(arr, diag=0) → submat¶
Returns one of array diagonals.
Parameters:
The function returns the header, corresponding to a specified diagonal of the input array.
GetDims¶
The function returns a list of array dimensions. In the case of IplImage or CvMat it always returns a list of length 2.
GetElemType¶
The function returns type of the array elements as described in CreateMat discussion: CV_8UC1 ... CV_64FC4 .
GetImage¶
- GetImage(arr) → iplimage¶
Returns image header for arbitrary array.
Parameters: arr (CvMat) – Input array
The function returns the image header for the input array that can be a matrix - CvMat , or an image - IplImage* . In the case of an image the function simply returns the input pointer. In the case of CvMat it initializes an imageHeader structure with the parameters of the input matrix. Note that if we transform IplImage to CvMat and then transform CvMat back to IplImage, we can get different headers if the ROI is set, and thus some IPL functions that calculate image stride from its width and align may fail on the resultant image.
GetImageCOI¶
- GetImageCOI(image) → channel¶
Returns the index of the channel of interest.
Parameters: image (IplImage) – A pointer to the image header
Returns the channel of interest of in an IplImage. Returned values correspond to the coi in SetImageCOI .
GetImageROI¶
- GetImageROI(image) → CvRect¶
Returns the image ROI.
Parameters: image (IplImage) – A pointer to the image header
If there is no ROI set, cvRect(0,0,image->width,image->height) is returned.
GetMat¶
- GetMat(arr, allowND=0) → cvmat¶
Returns matrix header for arbitrary array.
Parameters: - arr (IplImage) – Input array
- allowND (int) – If non-zero, the function accepts multi-dimensional dense arrays (CvMatND*) and returns 2D (if CvMatND has two dimensions) or 1D matrix (when CvMatND has 1 dimension or more than 2 dimensions). The array must be continuous.
The function returns a matrix header for the input array that can be a matrix -
CvMat , an image - IplImage or a multi-dimensional dense array - CvMatND (latter case is allowed only if allowND != 0 ) . In the case of matrix the function simply returns the input pointer. In the case of IplImage* or CvMatND it initializes the header structure with parameters of the current image ROI and returns the pointer to this temporary structure. Because COI is not supported by CvMat , it is returned separately.
The function provides an easy way to handle both types of arrays - IplImage and CvMat - using the same code. Reverse transform from CvMat to IplImage can be done using the GetImage function.
Input array must have underlying data allocated or attached, otherwise the function fails.
If the input array is IplImage with planar data layout and COI set, the function returns the pointer to the selected plane and COI = 0. It enables per-plane processing of multi-channel images with planar data layout using OpenCV functions.
GetOptimalDFTSize¶
- GetOptimalDFTSize(size0) → int¶
Returns optimal DFT size for a given vector size.
Parameters: size0 (int) – Vector size
The function returns the minimum number
N
that is greater than or equal to
size0
, such that the DFT
of a vector of size
N
can be computed fast. In the current
implementation
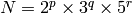 , for some
, for some
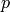 ,
,
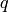 ,
,
 .
.
The function returns a negative number if size0 is too large (very close to INT_MAX )
GetReal1D¶
- GetReal1D(arr, idx0) → float¶
Return a specific element of single-channel 1D array.
Parameters: - arr (CvArr) – Input array. Must have a single channel.
- idx0 (int) – The first zero-based component of the element index
Returns a specific element of a single-channel array. If the array has multiple channels, a runtime error is raised. Note that Get function can be used safely for both single-channel and multiple-channel arrays though they are a bit slower.
In the case of a sparse array the functions return 0 if the requested node does not exist (no new node is created by the functions).
GetReal2D¶
- GetReal2D(arr, idx0, idx1) → float¶
Return a specific element of single-channel 2D array.
Parameters: - arr (CvArr) – Input array. Must have a single channel.
- idx0 (int) – The first zero-based component of the element index
- idx1 (int) – The second zero-based component of the element index
Returns a specific element of a single-channel array. If the array has multiple channels, a runtime error is raised. Note that Get function can be used safely for both single-channel and multiple-channel arrays though they are a bit slower.
In the case of a sparse array the functions return 0 if the requested node does not exist (no new node is created by the functions).
GetReal3D¶
- GetReal3D(arr, idx0, idx1, idx2) → float¶
Return a specific element of single-channel array.
Parameters: - arr (CvArr) – Input array. Must have a single channel.
- idx0 (int) – The first zero-based component of the element index
- idx1 (int) – The second zero-based component of the element index
- idx2 (int) – The third zero-based component of the element index
Returns a specific element of a single-channel array. If the array has multiple channels, a runtime error is raised. Note that Get function can be used safely for both single-channel and multiple-channel arrays though they are a bit slower.
In the case of a sparse array the functions return 0 if the requested node does not exist (no new node is created by the functions).
GetRealND¶
- GetRealND(arr, idx) → float¶
Return a specific element of single-channel array.
Parameters: - arr (CvArr) – Input array. Must have a single channel.
- idx (sequence of int) – Array of the element indices
Returns a specific element of a single-channel array. If the array has multiple channels, a runtime error is raised. Note that Get function can be used safely for both single-channel and multiple-channel arrays though they are a bit slower.
In the case of a sparse array the functions return 0 if the requested node does not exist (no new node is created by the functions).
GetRow¶
- GetRow(arr, row) → submat¶
Returns array row.
Parameters:
The function GetRow returns a single row from the input array.
GetRows¶
- GetRows(arr, startRow, endRow, deltaRow=1) → submat¶
Returns array row span.
Parameters:
The function GetRows returns a row span from the input array.
GetSize¶
The function returns number of rows (CvSize::height) and number of columns (CvSize::width) of the input matrix or image. In the case of image the size of ROI is returned.
GetSubRect¶
- GetSubRect(arr, rect) → cvmat¶
Returns matrix header corresponding to the rectangular sub-array of input image or matrix.
Parameters:
The function returns header, corresponding to a specified rectangle of the input array. In other words, it allows the user to treat a rectangular part of input array as a stand-alone array. ROI is taken into account by the function so the sub-array of ROI is actually extracted.
InRange¶
- InRange(src, lower, upper, dst) → None¶
Checks that array elements lie between the elements of two other arrays.
Parameters:
The function does the range check for every element of the input array:
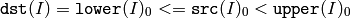
For single-channel arrays,
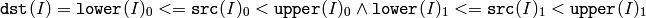
For two-channel arrays and so forth,
dst(I) is set to 0xff (all 1 -bits) if src(I) is within the range and 0 otherwise. All the arrays must have the same type, except the destination, and the same size (or ROI size).
InRangeS¶
- InRangeS(src, lower, upper, dst) → None¶
Checks that array elements lie between two scalars.
Parameters:
The function does the range check for every element of the input array:
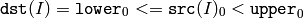
For single-channel arrays,
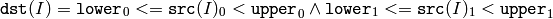
For two-channel arrays nd so forth,
‘dst(I)’ is set to 0xff (all 1 -bits) if ‘src(I)’ is within the range and 0 otherwise. All the arrays must have the same size (or ROI size).
InvSqrt¶
- InvSqrt(value) → float¶
Calculates the inverse square root.
Parameters: value (float) – The input floating-point value
The function calculates the inverse square root of the argument, and normally it is faster than
1./sqrt(value)
. If the argument is zero or negative, the result is not determined. Special values (
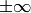 , NaN) are not handled.
, NaN) are not handled.
Inv¶
Invert
- Invert(src, dst, method=CV_LU) → double¶
Finds the inverse or pseudo-inverse of a matrix.
Parameters: - src – The source matrix
- dst – The destination matrix
- method –
Inversion method
- CV_LU Gaussian elimination with optimal pivot element chosen
- CV_SVD Singular value decomposition (SVD) method
- CV_SVD_SYM SVD method for a symmetric positively-defined matrix
The function inverts matrix src1 and stores the result in src2 .
In the case of LU method, the function returns the src1 determinant (src1 must be square). If it is 0, the matrix is not inverted and src2 is filled with zeros.
In the case of SVD methods, the function returns the inversed condition of src1 (ratio of the smallest singular value to the largest singular value) and 0 if src1 is all zeros. The SVD methods calculate a pseudo-inverse matrix if src1 is singular.
IsInf¶
- IsInf(value) → int¶
Determines if the argument is Infinity.
Parameters: value (float) – The input floating-point value
The function returns 1 if the argument is
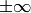 (as defined by IEEE754 standard), 0 otherwise.
(as defined by IEEE754 standard), 0 otherwise.
IsNaN¶
- IsNaN(value) → int¶
Determines if the argument is Not A Number.
Parameters: value (float) – The input floating-point value
The function returns 1 if the argument is Not A Number (as defined by IEEE754 standard), 0 otherwise.
LUT¶
- LUT(src, dst, lut) → None¶
Performs a look-up table transform of an array.
Parameters: - src (CvArr) – Source array of 8-bit elements
- dst (CvArr) – Destination array of a given depth and of the same number of channels as the source array
- lut (CvArr) – Look-up table of 256 elements; should have the same depth as the destination array. In the case of multi-channel source and destination arrays, the table should either have a single-channel (in this case the same table is used for all channels) or the same number of channels as the source/destination array.
The function fills the destination array with values from the look-up table. Indices of the entries are taken from the source array. That is, the function processes each element of src as follows:
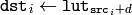
where
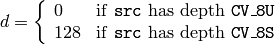
Log¶
- Log(src, dst) → None¶
Calculates the natural logarithm of every array element’s absolute value.
Parameters:
The function calculates the natural logarithm of the absolute value of every element of the input array:
![\texttt{dst} [I] = \fork{\log{|\texttt{src}(I)}}{if $\texttt{src}[I] \ne 0$ }{\texttt{C}}{otherwise}](_images/math/c9674a87d0835e8caabdc2f257e50624032b3264.png)
Where C is a large negative number (about -700 in the current implementation).
Mahalanobis¶
- Mahalonobis(vec1, vec2, mat) → None¶
Calculates the Mahalanobis distance between two vectors.
Parameters: - vec1 – The first 1D source vector
- vec2 – The second 1D source vector
- mat – The inverse covariance matrix
The function calculates and returns the weighted distance between two vectors:
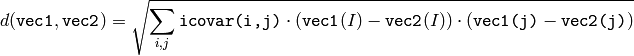
The covariance matrix may be calculated using the CalcCovarMatrix function and further inverted using the Invert function (CV _ SVD method is the prefered one because the matrix might be singular).
Max¶
- Max(src1, src2, dst) → None¶
Finds per-element maximum of two arrays.
Parameters:
The function calculates per-element maximum of two arrays:
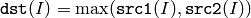
All the arrays must have a single channel, the same data type and the same size (or ROI size).
MaxS¶
- MaxS(src, value, dst) → None¶
Finds per-element maximum of array and scalar.
Parameters:
The function calculates per-element maximum of array and scalar:
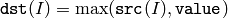
All the arrays must have a single channel, the same data type and the same size (or ROI size).
Merge¶
- Merge(src0, src1, src2, src3, dst) → None¶
Composes a multi-channel array from several single-channel arrays or inserts a single channel into the array.
Parameters:
The function is the opposite to Split . If the destination array has N channels then if the first N input channels are not NULL, they all are copied to the destination array; if only a single source channel of the first N is not NULL, this particular channel is copied into the destination array; otherwise an error is raised. The rest of the source channels (beyond the first N) must always be NULL. For IplImage Copy with COI set can be also used to insert a single channel into the image.
Min¶
- Min(src1, src2, dst) → None¶
Finds per-element minimum of two arrays.
Parameters:
The function calculates per-element minimum of two arrays:
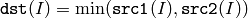
All the arrays must have a single channel, the same data type and the same size (or ROI size).
MinMaxLoc¶
- MinMaxLoc(arr, mask=NULL)-> (minVal, maxVal, minLoc, maxLoc)¶
Finds global minimum and maximum in array or subarray.
Parameters: - arr (CvArr) – The source array, single-channel or multi-channel with COI set
- minVal (float) – Pointer to returned minimum value
- maxVal (float) – Pointer to returned maximum value
- minLoc (CvPoint) – Pointer to returned minimum location
- maxLoc (CvPoint) – Pointer to returned maximum location
- mask (CvArr) – The optional mask used to select a subarray
The function finds minimum and maximum element values and their positions. The extremums are searched across the whole array, selected ROI (in the case of IplImage ) or, if mask is not NULL , in the specified array region. If the array has more than one channel, it must be IplImage with COI set. In the case of multi-dimensional arrays, minLoc->x and maxLoc->x will contain raw (linear) positions of the extremums.
MinS¶
- MinS(src, value, dst) → None¶
Finds per-element minimum of an array and a scalar.
Parameters:
The function calculates minimum of an array and a scalar:
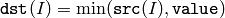
All the arrays must have a single channel, the same data type and the same size (or ROI size).
MixChannels¶
- MixChannels(src, dst, fromTo) → None¶
Copies several channels from input arrays to certain channels of output arrays
Parameters: - src (cvarr_count) – Input arrays
- dst (cvarr_count) – Destination arrays
- fromTo (intpair) –
The array of pairs of indices of the planes copied. Each pair fromTo[k]=(i,j) means that i-th plane from src is copied to the j-th plane in dst , where continuous plane numbering is used both in the input array list and the output array list. As a special case, when the fromTo[k][0] is negative, the corresponding output plane j
is filled with zero.
The function is a generalized form of cvSplit and Merge and some forms of CvtColor . It can be used to change the order of the planes, add/remove alpha channel, extract or insert a single plane or multiple planes etc.
As an example, this code splits a 4-channel RGBA image into a 3-channel BGR (i.e. with R and B swapped) and separate alpha channel image:
rgba = cv.CreateMat(100, 100, cv.CV_8UC4)
bgr = cv.CreateMat(100, 100, cv.CV_8UC3)
alpha = cv.CreateMat(100, 100, cv.CV_8UC1)
cv.Set(rgba, (1,2,3,4))
cv.MixChannels([rgba], [bgr, alpha], [
(0, 2), # rgba[0] -> bgr[2]
(1, 1), # rgba[1] -> bgr[1]
(2, 0), # rgba[2] -> bgr[0]
(3, 3) # rgba[3] -> alpha[0]
])
Mul¶
- Mul(src1, src2, dst, scale) → None¶
Calculates the per-element product of two arrays.
Parameters:
The function calculates the per-element product of two arrays:
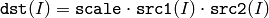
All the arrays must have the same type and the same size (or ROI size). For types that have limited range this operation is saturating.
MulSpectrums¶
- MulSpectrums(src1, src2, dst, flags) → None¶
Performs per-element multiplication of two Fourier spectrums.
Parameters: - src1 (CvArr) – The first source array
- src2 (CvArr) – The second source array
- dst (CvArr) – The destination array of the same type and the same size as the source arrays
- flags (int) –
A combination of the following values;
- CV_DXT_ROWS treats each row of the arrays as a separate spectrum (see DFT parameters description).
- CV_DXT_MUL_CONJ conjugate the second source array before the multiplication.
The function performs per-element multiplication of the two CCS-packed or complex matrices that are results of a real or complex Fourier transform.
The function, together with DFT , may be used to calculate convolution of two arrays rapidly.
MulTransposed¶
- MulTransposed(src, dst, order, delta=NULL, scale) → None¶
Calculates the product of an array and a transposed array.
Parameters:
The function calculates the product of src and its transposition:
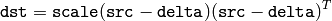
if
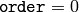 , and
, and
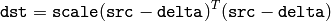
otherwise.
Norm¶
- Norm(arr1, arr2, normType=CV_L2, mask=NULL) → double¶
Calculates absolute array norm, absolute difference norm, or relative difference norm.
Parameters:
The function calculates the absolute norm of arr1 if arr2 is NULL:
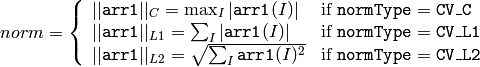
or the absolute difference norm if arr2 is not NULL:
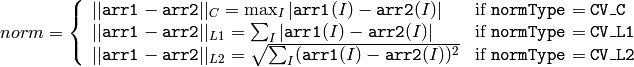
or the relative difference norm if arr2 is not NULL and (normType & CV_RELATIVE) != 0 :

The function returns the calculated norm. A multiple-channel array is treated as a single-channel, that is, the results for all channels are combined.
Not¶
- Not(src, dst) → None¶
Performs per-element bit-wise inversion of array elements.
Parameters:
The function Not inverses every bit of every array element:
dst(I)=~src(I)
Or¶
- Or(src1, src2, dst, mask=NULL) → None¶
Calculates per-element bit-wise disjunction of two arrays.
Parameters:
The function calculates per-element bit-wise disjunction of two arrays:
dst(I)=src1(I)|src2(I)
In the case of floating-point arrays their bit representations are used for the operation. All the arrays must have the same type, except the mask, and the same size.
OrS¶
- OrS(src, value, dst, mask=NULL) → None¶
Calculates a per-element bit-wise disjunction of an array and a scalar.
Parameters:
The function OrS calculates per-element bit-wise disjunction of an array and a scalar:
dst(I)=src(I)|value if mask(I)!=0
Prior to the actual operation, the scalar is converted to the same type as that of the array(s). In the case of floating-point arrays their bit representations are used for the operation. All the arrays must have the same type, except the mask, and the same size.
PerspectiveTransform¶
- PerspectiveTransform(src, dst, mat) → None¶
Performs perspective matrix transformation of a vector array.
Parameters:
The function transforms every element of src (by treating it as 2D or 3D vector) in the following way:
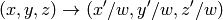
where
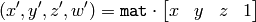
and
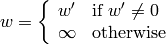
PolarToCart¶
- PolarToCart(magnitude, angle, x, y, angleInDegrees=0) → None¶
Calculates Cartesian coordinates of 2d vectors represented in polar form.
Parameters: - magnitude (CvArr) – The array of magnitudes. If it is NULL, the magnitudes are assumed to be all 1’s.
- angle (CvArr) – The array of angles, whether in radians or degrees
- x (CvArr) – The destination array of x-coordinates, may be set to NULL if it is not needed
- y (CvArr) – The destination array of y-coordinates, mau be set to NULL if it is not needed
- angleInDegrees (int) – The flag indicating whether the angles are measured in radians, which is default mode, or in degrees
The function calculates either the x-coodinate, y-coordinate or both of every vector magnitude(I)*exp(angle(I)*j), j=sqrt(-1) :
x(I)=magnitude(I)*cos(angle(I)),
y(I)=magnitude(I)*sin(angle(I))
Pow¶
- Pow(src, dst, power) → None¶
Raises every array element to a power.
Parameters:
The function raises every element of the input array to p :
![\texttt{dst} [I] = \fork{\texttt{src}(I)^p}{if \texttt{p} is integer}{|\texttt{src}(I)^p|}{otherwise}](_images/math/dce163a41d9683729fbdfeb68bf27fef04a12709.png)
That is, for a non-integer power exponent the absolute values of input array elements are used. However, it is possible to get true values for negative values using some extra operations, as the following example, computing the cube root of array elements, shows:
>>> import cv
>>> src = cv.CreateMat(1, 10, cv.CV_32FC1)
>>> mask = cv.CreateMat(src.rows, src.cols, cv.CV_8UC1)
>>> dst = cv.CreateMat(src.rows, src.cols, cv.CV_32FC1)
>>> cv.CmpS(src, 0, mask, cv.CV_CMP_LT) # find negative elements
>>> cv.Pow(src, dst, 1. / 3)
>>> cv.SubRS(dst, cv.ScalarAll(0), dst, mask) # negate the results of negative inputs
For some values of power , such as integer values, 0.5, and -0.5, specialized faster algorithms are used.
RNG¶
- RNG(seed=-1LL) → CvRNG¶
Initializes a random number generator state.
Parameters: seed (int64) – 64-bit value used to initiate a random sequence
The function initializes a random number generator and returns the state. The pointer to the state can be then passed to the RandInt , RandReal and RandArr functions. In the current implementation a multiply-with-carry generator is used.
RandArr¶
- RandArr(rng, arr, distType, param1, param2) → None¶
Fills an array with random numbers and updates the RNG state.
Parameters: - rng (CvRNG) – RNG state initialized by RNG
- arr (CvArr) – The destination array
- distType (int) –
Distribution type
- CV_RAND_UNI uniform distribution
- CV_RAND_NORMAL normal or Gaussian distribution
- param1 (CvScalar) – The first parameter of the distribution. In the case of a uniform distribution it is the inclusive lower boundary of the random numbers range. In the case of a normal distribution it is the mean value of the random numbers.
- param2 (CvScalar) – The second parameter of the distribution. In the case of a uniform distribution it is the exclusive upper boundary of the random numbers range. In the case of a normal distribution it is the standard deviation of the random numbers.
The function fills the destination array with uniformly or normally distributed random numbers.
RandInt¶
- RandInt(rng) → unsigned¶
Returns a 32-bit unsigned integer and updates RNG.
Parameters: rng (CvRNG) – RNG state initialized by RandInit and, optionally, customized by RandSetRange (though, the latter function does not affect the discussed function outcome)
The function returns a uniformly-distributed random
32-bit unsigned integer and updates the RNG state. It is similar to the rand()
function from the C runtime library, but it always generates a 32-bit number
whereas rand() returns a number in between 0 and
RAND_MAX
which is
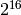 or
or
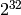 , depending on the platform.
, depending on the platform.
The function is useful for generating scalar random numbers, such as points, patch sizes, table indices, etc., where integer numbers of a certain range can be generated using a modulo operation and floating-point numbers can be generated by scaling from 0 to 1 or any other specific range.
RandReal¶
- RandReal(rng) → double¶
Returns a floating-point random number and updates RNG.
Parameters: rng (CvRNG) – RNG state initialized by RNG
The function returns a uniformly-distributed random floating-point number between 0 and 1 (1 is not included).
Reduce¶
- Reduce(src, dst, dim=-1, op=CV_REDUCE_SUM) → None¶
Reduces a matrix to a vector.
Parameters: - src (CvArr) – The input matrix.
- dst (CvArr) – The output single-row/single-column vector that accumulates somehow all the matrix rows/columns.
- dim (int) – The dimension index along which the matrix is reduced. 0 means that the matrix is reduced to a single row, 1 means that the matrix is reduced to a single column and -1 means that the dimension is chosen automatically by analysing the dst size.
- op (int) –
The reduction operation. It can take of the following values:
- CV_REDUCE_SUM The output is the sum of all of the matrix’s rows/columns.
- CV_REDUCE_AVG The output is the mean vector of all of the matrix’s rows/columns.
- CV_REDUCE_MAX The output is the maximum (column/row-wise) of all of the matrix’s rows/columns.
- CV_REDUCE_MIN The output is the minimum (column/row-wise) of all of the matrix’s rows/columns.
The function reduces matrix to a vector by treating the matrix rows/columns as a set of 1D vectors and performing the specified operation on the vectors until a single row/column is obtained. For example, the function can be used to compute horizontal and vertical projections of an raster image. In the case of CV_REDUCE_SUM and CV_REDUCE_AVG the output may have a larger element bit-depth to preserve accuracy. And multi-channel arrays are also supported in these two reduction modes.
Repeat¶
- Repeat(src, dst) → None¶
Fill the destination array with repeated copies of the source array.
Parameters:
The function fills the destination array with repeated copies of the source array:
dst(i,j)=src(i mod rows(src), j mod cols(src))
So the destination array may be as larger as well as smaller than the source array.
ResetImageROI¶
- ResetImageROI(image) → None¶
Resets the image ROI to include the entire image and releases the ROI structure.
Parameters: image (IplImage) – A pointer to the image header
This produces a similar result to the following
cv.SetImageROI(image, (0, 0, image.width, image.height))
cv.SetImageCOI(image, 0)
Reshape¶
- Reshape(arr, newCn, newRows=0) → cvmat¶
Changes shape of matrix/image without copying data.
Parameters: - arr (CvArr) – Input array
- newCn (int) – New number of channels. ‘newCn = 0’ means that the number of channels remains unchanged.
- newRows (int) – New number of rows. ‘newRows = 0’ means that the number of rows remains unchanged unless it needs to be changed according to newCn value.
The function initializes the CvMat header so that it points to the same data as the original array but has a different shape - different number of channels, different number of rows, or both.
ReshapeMatND¶
- ReshapeMatND(arr, newCn, newDims) → cvmat¶
Changes the shape of a multi-dimensional array without copying the data.
Parameters: - arr (CvMat) – Input array
- newCn (int) – New number of channels.
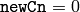 means that the number of channels remains unchanged.
means that the number of channels remains unchanged. - newDims (sequence of int) – List of new dimensions.
Returns a new CvMatND that shares the same data as arr but has different dimensions or number of channels. The only requirement is that the total length of the data is unchanged.
>>> import cv
>>> mat = cv.CreateMatND([24], cv.CV_32FC1)
>>> print cv.GetDims(cv.ReshapeMatND(mat, 0, [8, 3]))
(8, 3)
>>> m2 = cv.ReshapeMatND(mat, 4, [3, 2])
>>> print cv.GetDims(m2)
(3, 2)
>>> print m2.channels
4
Round¶
- Round(value) → int¶
Converts a floating-point number to the nearest integer value.
Parameters: value (float) – The input floating-point value
On some architectures this function is much faster than the standard cast
operations. If the absolute value of the argument is greater than
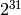 , the result is not determined. Special values (
, the result is not determined. Special values (
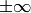 , NaN)
are not handled.
, NaN)
are not handled.
Floor¶
- Floor(value) → int¶
Converts a floating-point number to the nearest integer value that is not larger than the argument.
Parameters: value (float) – The input floating-point value
On some architectures this function is much faster than the standard cast
operations. If the absolute value of the argument is greater than
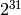 , the result is not determined. Special values (
, the result is not determined. Special values (
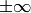 , NaN)
are not handled.
, NaN)
are not handled.
Ceil¶
- Ceil(value) → int¶
Converts a floating-point number to the nearest integer value that is not smaller than the argument.
Parameters: value (float) – The input floating-point value
On some architectures this function is much faster than the standard cast
operations. If the absolute value of the argument is greater than
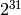 , the result is not determined. Special values (
, the result is not determined. Special values (
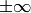 , NaN)
are not handled.
, NaN)
are not handled.
ScaleAdd¶
- ScaleAdd(src1, scale, src2, dst) → None¶
Calculates the sum of a scaled array and another array.
Parameters:
The function calculates the sum of a scaled array and another array:
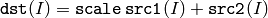
All array parameters should have the same type and the same size.
Set¶
- Set(arr, value, mask=NULL) → None¶
Sets every element of an array to a given value.
Parameters:
The function copies the scalar value to every selected element of the destination array:
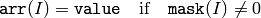
If array arr is of IplImage type, then is ROI used, but COI must not be set.
Set1D¶
- Set1D(arr, idx, value) → None¶
Set a specific array element.
Parameters:
Sets a specific array element. Array must have dimension 1.
Set2D¶
- Set2D(arr, idx0, idx1, value) → None¶
Set a specific array element.
Parameters:
Sets a specific array element. Array must have dimension 2.
Set3D¶
- Set3D(arr, idx0, idx1, idx2, value) → None¶
Set a specific array element.
Parameters:
Sets a specific array element. Array must have dimension 3.
SetND¶
- SetND(arr, indices, value) → None¶
Set a specific array element.
Parameters:
Sets a specific array element. The length of array indices must be the same as the dimension of the array.
SetData¶
- SetData(arr, data, step) → None¶
Assigns user data to the array header.
Parameters: - arr (CvArr) – Array header
- data (object) – User data
- step (int) – Full row length in bytes
The function assigns user data to the array header. Header should be initialized before using cvCreate*Header , cvInit*Header or Mat (in the case of matrix) function.
SetIdentity¶
- SetIdentity(mat, value=1) → None¶
Initializes a scaled identity matrix.
Parameters:
The function initializes a scaled identity matrix:
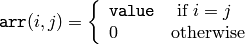
SetImageCOI¶
- SetImageCOI(image, coi) → None¶
Sets the channel of interest in an IplImage.
Parameters: - image (IplImage) – A pointer to the image header
- coi (int) – The channel of interest. 0 - all channels are selected, 1 - first channel is selected, etc. Note that the channel indices become 1-based.
If the ROI is set to NULL and the coi is not 0, the ROI is allocated. Most OpenCV functions do not support the COI setting, so to process an individual image/matrix channel one may copy (via Copy or Split ) the channel to a separate image/matrix, process it and then copy the result back (via Copy or Merge ) if needed.
SetImageROI¶
- SetImageROI(image, rect) → None¶
Sets an image Region Of Interest (ROI) for a given rectangle.
Parameters:
If the original image ROI was NULL and the rect is not the whole image, the ROI structure is allocated.
Most OpenCV functions support the use of ROI and treat the image rectangle as a separate image. For example, all of the pixel coordinates are counted from the top-left (or bottom-left) corner of the ROI, not the original image.
SetReal1D¶
- SetReal1D(arr, idx, value) → None¶
Set a specific array element.
Parameters: - arr (CvArr) – Input array
- idx (int) – Zero-based element index
- value (float) – The value to assign to the element
Sets a specific array element. Array must have dimension 1.
SetReal2D¶
- SetReal2D(arr, idx0, idx1, value) → None¶
Set a specific array element.
Parameters: - arr (CvArr) – Input array
- idx0 (int) – Zero-based element row index
- idx1 (int) – Zero-based element column index
- value (float) – The value to assign to the element
Sets a specific array element. Array must have dimension 2.
SetReal3D¶
- SetReal3D(arr, idx0, idx1, idx2, value) → None¶
Set a specific array element.
Parameters: - arr (CvArr) – Input array
- idx0 (int) – Zero-based element index
- idx1 (int) – Zero-based element index
- idx2 (int) – Zero-based element index
- value (float) – The value to assign to the element
Sets a specific array element. Array must have dimension 3.
SetRealND¶
- SetRealND(arr, indices, value) → None¶
Set a specific array element.
Parameters: - arr (CvArr) – Input array
- indices (sequence of int) – List of zero-based element indices
- value (float) – The value to assign to the element
Sets a specific array element. The length of array indices must be the same as the dimension of the array.
SetZero¶
The function clears the array. In the case of dense arrays (CvMat, CvMatND or IplImage), cvZero(array) is equivalent to cvSet(array,cvScalarAll(0),0). In the case of sparse arrays all the elements are removed.
Solve¶
- Solve(A, B, X, method=CV_LU) → None¶
Solves a linear system or least-squares problem.
Parameters: - A (CvArr) – The source matrix
- B (CvArr) – The right-hand part of the linear system
- X (CvArr) – The output solution
- method (int) –
The solution (matrix inversion) method
- CV_LU Gaussian elimination with optimal pivot element chosen
- CV_SVD Singular value decomposition (SVD) method
- CV_SVD_SYM SVD method for a symmetric positively-defined matrix.
The function solves a linear system or least-squares problem (the latter is possible with SVD methods):
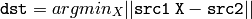
If CV_LU method is used, the function returns 1 if src1 is non-singular and 0 otherwise; in the latter case dst is not valid.
SolveCubic¶
- SolveCubic(coeffs, roots) → None¶
Finds the real roots of a cubic equation.
Parameters:
The function finds the real roots of a cubic equation:
If coeffs is a 4-element vector:
![\texttt{coeffs} [0] x^3 + \texttt{coeffs} [1] x^2 + \texttt{coeffs} [2] x + \texttt{coeffs} [3] = 0](_images/math/fe7795e1b29e8f68c0ede218705289b0674bba6b.png)
or if coeffs is 3-element vector:
![x^3 + \texttt{coeffs} [0] x^2 + \texttt{coeffs} [1] x + \texttt{coeffs} [2] = 0](_images/math/ba956f7c22249ea7674f92cbab534fde659bd964.png)
The function returns the number of real roots found. The roots are stored to root array, which is padded with zeros if there is only one root.
Split¶
- Split(src, dst0, dst1, dst2, dst3) → None¶
Divides multi-channel array into several single-channel arrays or extracts a single channel from the array.
Parameters:
The function divides a multi-channel array into separate single-channel arrays. Two modes are available for the operation. If the source array has N channels then if the first N destination channels are not NULL, they all are extracted from the source array; if only a single destination channel of the first N is not NULL, this particular channel is extracted; otherwise an error is raised. The rest of the destination channels (beyond the first N) must always be NULL. For IplImage Copy with COI set can be also used to extract a single channel from the image.
Sqrt¶
- Sqrt(value) → float¶
Calculates the square root.
Parameters: value (float) – The input floating-point value
The function calculates the square root of the argument. If the argument is negative, the result is not determined.
Sub¶
- Sub(src1, src2, dst, mask=NULL) → None¶
Computes the per-element difference between two arrays.
Parameters:
The function subtracts one array from another one:
dst(I)=src1(I)-src2(I) if mask(I)!=0
All the arrays must have the same type, except the mask, and the same size (or ROI size). For types that have limited range this operation is saturating.
SubRS¶
- SubRS(src, value, dst, mask=NULL) → None¶
Computes the difference between a scalar and an array.
Parameters:
The function subtracts every element of source array from a scalar:
dst(I)=value-src(I) if mask(I)!=0
All the arrays must have the same type, except the mask, and the same size (or ROI size). For types that have limited range this operation is saturating.
SubS¶
- SubS(src, value, dst, mask=NULL) → None¶
Computes the difference between an array and a scalar.
Parameters:
The function subtracts a scalar from every element of the source array:
dst(I)=src(I)-value if mask(I)!=0
All the arrays must have the same type, except the mask, and the same size (or ROI size). For types that have limited range this operation is saturating.
Sum¶
The function calculates the sum S of array elements, independently for each channel:
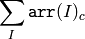
If the array is IplImage and COI is set, the function processes the selected channel only and stores the sum to the first scalar component.
SVBkSb¶
- SVBkSb(W, U, V, B, X, flags) → None¶
Performs singular value back substitution.
Parameters: - W (CvArr) – Matrix or vector of singular values
- U (CvArr) – Left orthogonal matrix (tranposed, perhaps)
- V (CvArr) – Right orthogonal matrix (tranposed, perhaps)
- B (CvArr) – The matrix to multiply the pseudo-inverse of the original matrix A by. This is an optional parameter. If it is omitted then it is assumed to be an identity matrix of an appropriate size (so that X will be the reconstructed pseudo-inverse of A ).
- X (CvArr) – The destination matrix: result of back substitution
- flags (int) – Operation flags, should match exactly to the flags passed to SVD
The function calculates back substitution for decomposed matrix A (see SVD description) and matrix B :
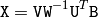
where
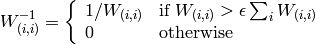
and
 is a small number that depends on the matrix data type.
is a small number that depends on the matrix data type.
This function together with SVD is used inside Invert and Solve , and the possible reason to use these (svd and bksb) “low-level” function, is to avoid allocation of temporary matrices inside the high-level counterparts (inv and solve).
SVD¶
- SVD(A, W, U = None, V = None, flags=0) → None¶
Performs singular value decomposition of a real floating-point matrix.
Parameters: - A (CvArr) – Source
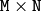 matrix
matrix - W (CvArr) – Resulting singular value diagonal matrix (
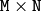 or
or 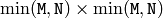 ) or
) or 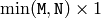 vector of the singular values
vector of the singular values - U (CvArr) – Optional left orthogonal matrix,
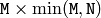 (when CV_SVD_U_T is not set), or
(when CV_SVD_U_T is not set), or 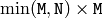 (when CV_SVD_U_T is set), or
(when CV_SVD_U_T is set), or 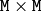 (regardless of CV_SVD_U_T flag).
(regardless of CV_SVD_U_T flag). - V (CvArr) – Optional right orthogonal matrix,
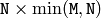 (when CV_SVD_V_T is not set), or
(when CV_SVD_V_T is not set), or 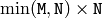 (when CV_SVD_V_T is set), or
(when CV_SVD_V_T is set), or 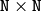 (regardless of CV_SVD_V_T flag).
(regardless of CV_SVD_V_T flag). - flags (int) –
Operation flags; can be 0 or a combination of the following values:
- CV_SVD_MODIFY_A enables modification of matrix A during the operation. It speeds up the processing.
- CV_SVD_U_T means that the transposed matrix U is returned. Specifying the flag speeds up the processing.
- CV_SVD_V_T means that the transposed matrix V is returned. Specifying the flag speeds up the processing.
- A (CvArr) – Source
The function decomposes matrix A into the product of a diagonal matrix and two
orthogonal matrices:
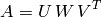
where
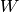 is a diagonal matrix of singular values that can be coded as a
1D vector of singular values and
is a diagonal matrix of singular values that can be coded as a
1D vector of singular values and
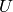 and
and
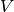 . All the singular values
are non-negative and sorted (together with
. All the singular values
are non-negative and sorted (together with
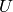 and
and
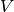 columns)
in descending order.
columns)
in descending order.
An SVD algorithm is numerically robust and its typical applications include:
accurate eigenvalue problem solution when matrix A is a square, symmetric, and positively defined matrix, for example, when
it is a covariance matrix.
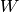 in this case will be a vector/matrix
in this case will be a vector/matrixof the eigenvalues, and
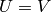 will be a matrix of the eigenvectors.
will be a matrix of the eigenvectors.accurate solution of a poor-conditioned linear system.
least-squares solution of an overdetermined linear system. This and the preceeding is done by using the Solve function with the CV_SVD method.
accurate calculation of different matrix characteristics such as the matrix rank (the number of non-zero singular values), condition number (ratio of the largest singular value to the smallest one), and determinant (absolute value of the determinant is equal to the product of singular values).
Transform¶
- Transform(src, dst, transmat, shiftvec=NULL) → None¶
Performs matrix transformation of every array element.
Parameters:
The function performs matrix transformation of every element of array src and stores the results in dst :
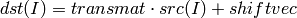
That is, every element of an
N
-channel array
src
is
considered as an
N
-element vector which is transformed using
a
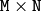 matrix
transmat
and shift
vector
shiftvec
into an element of
M
-channel array
dst
. There is an option to embedd
shiftvec
into
transmat
. In this case
transmat
should be a
matrix
transmat
and shift
vector
shiftvec
into an element of
M
-channel array
dst
. There is an option to embedd
shiftvec
into
transmat
. In this case
transmat
should be a
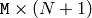 matrix and the rightmost column is treated as the shift
vector.
matrix and the rightmost column is treated as the shift
vector.
Both source and destination arrays should have the same depth and the same size or selected ROI size. transmat and shiftvec should be real floating-point matrices.
The function may be used for geometrical transformation of n dimensional point set, arbitrary linear color space transformation, shuffling the channels and so forth.
Transpose¶
- Transpose(src, dst) → None¶
Transposes a matrix.
Parameters:
The function transposes matrix src1 :
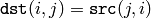
Note that no complex conjugation is done in the case of a complex matrix. Conjugation should be done separately: look at the sample code in XorS for an example.
Xor¶
- Xor(src1, src2, dst, mask=NULL) → None¶
Performs per-element bit-wise “exclusive or” operation on two arrays.
Parameters:
The function calculates per-element bit-wise logical conjunction of two arrays:
dst(I)=src1(I)^src2(I) if mask(I)!=0
In the case of floating-point arrays their bit representations are used for the operation. All the arrays must have the same type, except the mask, and the same size.
XorS¶
- XorS(src, value, dst, mask=NULL) → None¶
Performs per-element bit-wise “exclusive or” operation on an array and a scalar.
Parameters:
The function XorS calculates per-element bit-wise conjunction of an array and a scalar:
dst(I)=src(I)^value if mask(I)!=0
Prior to the actual operation, the scalar is converted to the same type as that of the array(s). In the case of floating-point arrays their bit representations are used for the operation. All the arrays must have the same type, except the mask, and the same size
mGet¶
- mGet(mat, row, col) → double¶
Returns the particular element of single-channel floating-point matrix.
Parameters: - mat (CvMat) – Input matrix
- row (int) – The zero-based index of row
- col (int) – The zero-based index of column
The function is a fast replacement for GetReal2D in the case of single-channel floating-point matrices. It is faster because it is inline, it does fewer checks for array type and array element type, and it checks for the row and column ranges only in debug mode.
mSet¶
- mSet(mat, row, col, value) → None¶
Returns a specific element of a single-channel floating-point matrix.
Parameters: - mat (CvMat) – The matrix
- row (int) – The zero-based index of row
- col (int) – The zero-based index of column
- value (float) – The new value of the matrix element
The function is a fast replacement for SetReal2D in the case of single-channel floating-point matrices. It is faster because it is inline, it does fewer checks for array type and array element type, and it checks for the row and column ranges only in debug mode.
Help and Feedback
You did not find what you were looking for?- Try the Cookbook.
- Ask a question in the user group/mailing list.
- If you think something is missing or wrong in the documentation, please file a bug report.
 or
or 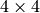 transformation matrix
transformation matrix