線形代数¶
行列要素の四則演算を行う¶
サイズや要素の型が異なる配列の場合,要素同士の演算はできません. 例外発生時のメッセージは,OpenCV のバージョンによって異なります.
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
// 3x3 の行列
cv::Mat m1 = (cv::Mat_<double>(3,3) << 1, 2, 3, 4, 5, 6, 7, 8, 9);
std::cout << "m1=" << m1 << std::endl << std::endl;
// 行列とスカラ
cv::Mat m2 = m1+3;
cv::Mat m3 = m1*3; // スケーリング
cv::Mat m4 = m1/3;
std::cout << "m2=" << m2 << std::endl << std::endl;
std::cout << "m3=" << m3 << std::endl << std::endl;
std::cout << "m4=" << m4 << std::endl << std::endl;
// 行列と行列
cv::Mat m5 = m1+m1;
cv::Mat m6 = m1.mul(m2); // m1*m2 とは違う
cv::Mat m7 = m1.mul(m2, 2); // スケールファクタ追加
std::cout << "m5=" << m5 << std::endl << std::endl;
std::cout << "m6=" << m6 << std::endl << std::endl;
std::cout << "m7=" << m7 << std::endl << std::endl;
// 要素の型が違う
cv::Mat m8 = (cv::Mat_<int>(3,3) << 1, 2, 3, 4, 5, 6, 7, 8, 9);
try {
std::cout << m1/m8 << std::endl;
} catch(cv::Exception e) {
// ...
std::cout << std::endl;
}
// 行列のサイズが違う
cv::Mat m9 = (cv::Mat_<double>(2,2) << 1, 2, 3, 4);
try {
std::cout << m9/m1 << std::endl;
} catch(cv::Exception e) {
// ...
std::cout << std::endl;
}
}
実行結果:
m1=[1, 2, 3;
4, 5, 6;
7, 8, 9]
m2=[4, 5, 6;
7, 8, 9;
10, 11, 12]
m3=[3, 6, 9;
12, 15, 18;
21, 24, 27]
m4=[0.3333333333333333, 0.6666666666666666, 1;
1.333333333333333, 1.666666666666667, 2;
2.333333333333333, 2.666666666666667, 3]
m5=[2, 4, 6;
8, 10, 12;
14, 16, 18]
m6=[4, 10, 18;
28, 40, 54;
70, 88, 108]
m7=[8, 20, 36;
56, 80, 108;
140, 176, 216]
OpenCV Error: Assertion failed (src1.size() == src2.size() && src1.type() == src2.type() && func != 0) in divide, file arithm.cpp, line 885
OpenCV Error: Assertion failed (src1.size() == src2.size() && src1.type() == src2.type() && func != 0) in divide, file arithm.cpp, line 885
行列同士の積を求める¶
前述の行列の「要素同士の積」とは異なり,* 演算子を利用すると,行列積を計算することができます. また,2チャンネルの行列は複素行列とみなされ,その積も複素行列積になることに注意してください.
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
// シングルチャンネル,3x3 の行列
cv::Mat m1 = (cv::Mat_<double>(3,3) << 1, 2, 3, 4, 5, 6, 7, 8, 9);
cv::Mat m2 = m1+3;
std::cout << "m1=" << m1 << std::endl << std::endl;
std::cout << "m2=" << m2 << std::endl << std::endl;
// 行列の積
std::cout << "m1*m2=" << m1*m2 << std::endl << std::endl;
cv::Mat m3 = (cv::Mat_<double>(3,3) << -1, 2, -3, 4, -5, 6, -7, 8, -9);
cv::Mat m4 = m3-3;
std::cout << "m3=" << m3 << std::endl << std::endl;
std::cout << "m4=" << m4 << std::endl << std::endl;
// 行列の積
std::cout << "m2*m4=" << m3*m4 << std::endl << std::endl;
// 2チャンネル,3x3 の行列
cv::Mat m13, m24;
std::vector<cv::Mat> ms(2);
ms[0] = m1;
ms[1] = m3;
cv::merge(ms, m13);
ms[0] = m2;
ms[1] = m4;
cv::merge(ms, m24);
// 複素行列の積
std::cout << "m13*m24=" << m13*m24 << std::endl;
}
実行結果:
m1=[1, 2, 3;
4, 5, 6;
7, 8, 9]
m2=[4, 5, 6;
7, 8, 9;
10, 11, 12]
m1*m2=[48, 54, 60;
111, 126, 141;
174, 198, 222]
m3=[-1, 2, -3;
4, -5, 6;
-7, 8, -9]
m4=[-4, -1, -6;
1, -8, 3;
-10, 5, -12]
m2*m4=[36, -30, 48;
-81, 66, -111;
126, -102, 174]
m13*m24=[12, -52, 84, -24, 12, -60;
192, -30, 60, 32, 252, -30;
48, -172, 300, -96, 48, -204]
cv::Vecの内積と外積¶
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
cv::Vec3d v1(1,2,3);
cv::Vec3d v2(3,4,5);
// 内積
double v_dot = v1.dot(v2);
// 外積(3要素ベクトル同士のみで計算可能)
cv::Vec3d v_cross = v1.cross(v2);
std::cout << "v_dot=" << v_dot << std::endl;
cv::Mat tmp(v_cross);
std::cout << "v_cross=" << tmp << std::endl;
}
実行結果:
v_dot=26
v_cross=[-2; 4; -2]
ノルムを求める¶
cv::Matやstd::vectorに対するL-2ノルムを計算します. また,Eigen::Matrix型に変換することで,任意のL-pノルムを簡単に求めることができます.
#include <iostream>
#include <iostream>
#include <Eigen/Core>
#include <opencv2/core/core.hpp>
#include <opencv2/core/eigen.hpp>
int
main(int argc, char *argv[])
{
// 6x1 の行列
cv::Mat m1 = (cv::Mat_<double>(6,1) << 1, 5, 3, -1,-3,-5);
// 2x3 の行列
cv::Mat m2 = (cv::Mat_<double>(2,3) << 1, 5, 3, -1,-3,-5);
// ベクトル(1,2,...,9)
std::vector<double> v1;
m1.copyTo(v1);
// ベクトル(3,4)
cv::Point p1(3,4);
double norm_m1 = cv::norm(m1); // 6次元ベクトルのL-2ノルム
double norm_m2 = cv::norm(m2); // 実数行列のフロベニウスノルム
// OpenCV>=2.3ならば, cv::norm(v1); で OK
double norm_v1 = cv::norm(cv::Mat(v1)); // 6次元ベクトルのL-2ノルム
double norm_p1 = cv::norm(p1); // 2次元ベクトルのL-2ノルム
std::cout << "norm(m1)=" << norm_m1 << std::endl;
std::cout << "norm(m2)=" << norm_m2 << std::endl;
std::cout << "norm(v1)=" << norm_v1 << std::endl;
std::cout << "norm(p1)=" << norm_p1 << std::endl << std::endl;
#if EIGEN_VERSION_AT_LEAST(2,2,0)
Eigen::VectorXd em1;
cv::cv2eigen(m1, em1);
double lpnorm1 = em1.lpNorm<1>(); // L-1ノルム
double lpnorm2 = em1.lpNorm<2>(); // L-2ノルム
double lpnorm3 = em1.lpNorm<3>(); // L-3ノルム
std::cout << "L-1 norm=" << lpnorm1 << std::endl;
std::cout << "L-2 norm=" << lpnorm2 << std::endl;
std::cout << "L-3 norm=" << lpnorm3 << std::endl;
#endif
}
実行結果:
norm(m1)=8.3666
norm(m2)=8.3666
norm(v1)=8.3666
norm(p1)=5
L-1 norm=18
L-2 norm=8.3666
L-3 norm=6.73866
行列式を求める¶
要素の型が CV_32FC1 または CV_64FC1 の正方行列の,行列式を求めます.
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
// 正方行列
cv::Mat m1 = (cv::Mat_<double>(3,3) << 1, 0, 3, 4, 5, 6, 7, 0, 9);
CV_Assert(m1.cols==m1.rows && (m1.type()==CV_32FC1 || m1.type()==CV_64FC1));
double d1 = cv::determinant(m1);
std::cout << "m1=" << m1 << std::endl;
std::cout << "det=" << d1 << std::endl << std::endl;
}
実行結果:
m1=[1, 0, 3;
4, 5, 6;
7, 0, 9]
det=-60
行列の転置¶
複素行列の転置は,共役転置行列( 随伴行列 )にはなりません.
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
// 3x1 行列
cv::Mat m1 = (cv::Mat_<double>(3,1) << 1, 2, 3);
std::cout << "m1=" << m1 << std::endl << std::endl;
std::cout << "m1.t()=" << m1.t() << std::endl << std::endl;
// 3x1 複素行列
std::complex<double> c1(1,2);
std::complex<double> c2(3,4);
std::complex<double> c3(5,6);
cv::Mat m2 = (cv::Mat_<std::complex<double> >(3, 1) << c1, c2, c3);
std::cout << "m2=" << m2 << std::endl << std::endl;
// 共役にはならない
std::cout << "m2.t()=" << m2.t() << std::endl << std::endl;
}
実行結果:
m1=[1; 2; 3]
m1.t()=[1, 2, 3]
m2=[1, 2; 3, 4; 5, 6]
m2.t()=[1, 2, 3, 4, 5, 6]
行列の対角成分を取り出す¶
2次元以外の Mat では, 対角成分 を取り出すことはできません.
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
// 5x5 の行列
cv::Mat m1 = (cv::Mat_<double>(5,5) << 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, \
11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25);
std::cout << "m1=" << m1 << std::endl << std::endl;
std::cout << "diag(0)=" << m1.diag(0) << std::endl << std::endl; // 主対角線上の成分
std::cout << "diag(1)=" << m1.diag(1) << std::endl << std::endl; // 主対角線の1つ上の成分
std::cout << "diag(-1)=" << m1.diag(-1) << std::endl << std::endl; // 主対角線の1つ下の成分
}
実行結果:
m1=[1, 2, 3, 4, 5;
6, 7, 8, 9, 10;
11, 12, 13, 14, 15;
16, 17, 18, 19, 20;
21, 22, 23, 24, 25]
diag(0)=[1; 7; 13; 19; 25]
diag(1)=[2; 8; 14; 20]
diag(-1)=[6; 12; 18; 24]
行列のトレースを求める¶
2次元以外の Mat では, トレース を求めることはできません.
シングルチャンネル行列のトレース¶
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
cv::Mat m1 = (cv::Mat_<int>(3,3) << 1,2,3,4,5,6,7,8,9);
std::cout << "m1=" << m1 << std::endl;
cv::Scalar traces = cv::trace(m1);
std::cout << "trace=" << traces[0] << std::endl << std::endl;
}
実行結果:
m1=[1, 2, 3;
4, 5, 6;
7, 8, 9]
trace=15
マルチチャンネル行列のトレース¶
2チャンネル行列の場合,要素は複素数として扱われ,実数部と虚数部のトレースが求められます.
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
cv::Mat m0 = (cv::Mat_<int>(3,6) << 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18);
// channels=2, 3x3 の行列
cv::Mat m1 = m0.reshape(2);
std::cout << "m1=" << m1 << std::endl << std::endl;
std::vector<cv::Mat> planes;
cv::Scalar traces = cv::trace(m1);
cv::split(m1, planes);
for(int i=0; i<m1.channels(); ++i) {
std::cout << planes[i] << std::endl;
std::cout << "trace[" << i << "]=" << traces[i] << std::endl << std::endl;
}
}
実行結果:
m1=[1, 2, 3, 4, 5, 6;
7, 8, 9, 10, 11, 12;
13, 14, 15, 16, 17, 18]
[1, 3, 5;
7, 9, 11;
13, 15, 17]
trace[0]=27
[2, 4, 6;
8, 10, 12;
14, 16, 18]
trace[1]=30
逆行列/疑似逆行列を求める¶
逆行列,あるいは疑似逆行列を求めます.
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
// 逆行列 (LU分解)
cv::Mat m1 = (cv::Mat_<double>(3,3) << 10, -9, -12, 7, -12, 11, -10, 10, 3);
std::cout << "m1=" << m1 << std::endl << std::endl;
std::cout << "inverse matrix (LU decompression):" << std::endl << std::endl;
std::cout << "m1^-1=" << m1.inv() << std::endl << std::endl;
std::cout << "m1*m1^-1=" << m1*m1.inv() << std::endl << std::endl;
// 逆行列 (SVD)
std::cout << "inverse matrix (SVD):" << std::endl << std::endl;
std::cout << "m1^-1=" << m1.inv(cv::DECOMP_SVD) << std::endl << std::endl;
std::cout << "m1*m1^-1=" << m1*m1.inv(cv::DECOMP_SVD) << std::endl << std::endl;
// 擬似逆行列
cv::Mat m2 = (cv::Mat_<double>(2,3) << 10, -9, -12, 7, -12, 11);
std::cout << "m2=" << m2 << std::endl << std::endl;
std::cout << "m2^-1=" << m2.inv(cv::DECOMP_SVD) << std::endl << std::endl;
std::cout << "m2*m2^-1=" << m2*m2.inv(cv::DECOMP_SVD) << std::endl << std::endl;
}
実行結果:
m1=[10, -9, -12;
7, -12, 11;
-10, 10, 3]
inverse matrix (LU decompression):
m1^-1=[-0.4576802507836991, -0.2915360501567398, -0.7617554858934169;
-0.4106583072100313, -0.2821316614420062, -0.6081504702194357;
-0.1567398119122257, -0.03134796238244514, -0.1786833855799373]
m1*m1^-1=[1, -4.996003610813204e-16, -3.33066907387547e-16;
-4.163336342344337e-16, 0.9999999999999996, -2.775557561562891e-16;
1.942890293094024e-16, 4.996003610813204e-16, 1]
inverse matrix (SVD):
m1^-1=[-0.4576802507837005, -0.2915360501567407, -0.7617554858934192;
-0.4106583072100324, -0.282131661442007, -0.6081504702194376;
-0.1567398119122261, -0.03134796238244537, -0.1786833855799379]
m1*m1^-1=[0.9999999999999998, 4.996003610813204e-16, 6.661338147750939e-16;
-1.165734175856414e-15, 0.9999999999999998, -6.661338147750939e-16;
2.442490654175344e-15, 9.020562075079397e-16, 1.000000000000003]
m2=[10, -9, -12;
7, -12, 11]
m2^-1=[0.02819861108331499, 0.01816198691136149;
-0.02275501831208597, -0.03488302279504472;
-0.04276822702983969, 0.04129725618908479]
m2*m2^-1=[1, -1.387778780781446e-17;
-1.040834085586084e-17, 0.9999999999999998]
2次元ベクトルの角度と大きさを求める¶
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
cv::Mat x = (cv::Mat_<double>(4,1) << 0, 1, 4, 1);
cv::Mat y = (cv::Mat_<double>(4,1) << 1, 1, 3, 1.7320504);
// 2次元座標から,大きさと角度を求める.
cv::Mat magnitude, angle;
cv::cartToPolar(x, y, magnitude, angle, true); // in degrees
for(int i=0; i<4; ++i) {
std::cout << "(" << x.at<double>(i) << ", " << y.at<double>(i) << ") ";
std::cout << "mag=" << magnitude.at<double>(i) << ", angle=" << angle.at<double>(i) << "[deg]" << std::endl;
}
}
実行結果:
(0, 1) mag=1, angle=90
(1, 1) mag=1.41421, angle=44.7623
(4, 3) mag=5, angle=37.1247
(1, 1.73205) mag=2, angle=59.7441
角度と大きさから2次元座標を求める¶
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
cv::Mat magnitude = (cv::Mat_<double>(4,1) << 1, 1.41421, 5, 2);
cv::Mat angle = (cv::Mat_<double>(4,1) << 90, 45, 36.8699, 60);
// 大きさと角度から,2次元座標を求める.
cv::Mat x, y;
cv::polarToCart(magnitude, angle, x, y, true); // in degrees
for(int i=0; i<4; ++i) {
std::cout << "(" << x.at<double>(i) << ", " << y.at<double>(i) << ") ";
std::cout << "mag=" << magnitude.at<double>(i) << ", angle=" << angle.at<double>(i) << "[deg]" << std::endl;
}
}
実行結果:
(2.65358e-17, 1) mag=1, angle=90[deg]
(0.999997, 0.999997) mag=1.41421, angle=45[deg]
(4, 3) mag=5, angle=36.8699[deg]
(1, 1.73205) mag=2, angle=60[deg]
行列を反転する¶
2次元以外の Mat では,flipを利用した反転行列を求めることはできません.
シングルチャンネル行列の反転¶
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
// 3x3 の行列
cv::Mat m1 = (cv::Mat_<double>(3,3) << 1, 2, 3, 4, 5, 6, 7, 8, 9);
cv::Mat mv, mh, mb;
cv::flip(m1, mv, 0); // 水平軸で反転
cv::flip(m1, mh, 1); // 垂直軸で反転
cv::flip(m1, mb, -1); // 両方の軸で反転
std::cout << "m1=" << m1 << std::endl << std::endl;
std::cout << "mv=" << mv << std::endl << std::endl;
std::cout << "mh=" << mh << std::endl << std::endl;
std::cout << "mb=" << mb << std::endl << std::endl;
}
実行結果:
m1=[1, 2, 3;
4, 5, 6;
7, 8, 9]
mv=[7, 8, 9;
4, 5, 6;
1, 2, 3]
mh=[3, 2, 1;
6, 5, 4;
9, 8, 7]
mb=[9, 8, 7;
6, 5, 4;
3, 2, 1]
マルチチャンネル行列の反転¶
マルチチャンネル行列の場合は,各チャンネル毎に反転が行われます. チャンネルの順番が入れ替わることはありません.
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
// CV32SC2, 3x3 行列(m1)
cv::Mat m0 = (cv::Mat_<int>(3,6) << 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18);
cv::Mat m1 = m0.reshape(2);
cv::Mat mv, mh, mb;
cv::flip(m1, mv, 0); // 水平軸で反転
cv::flip(m1, mh, 1); // 垂直軸で反転
cv::flip(m1, mb, -1); // 両方の軸で反転
std::cout << "m1=" << m1 << std::endl << std::endl;
std::cout << "mv=" << mv << std::endl << std::endl;
std::cout << "mh=" << mh << std::endl << std::endl;
std::cout << "mb=" << mb << std::endl << std::endl;
}
実行結果:
m1=[1, 2, 3, 4, 5, 6;
7, 8, 9, 10, 11, 12;
13, 14, 15, 16, 17, 18]
mv=[13, 14, 15, 16, 17, 18;
7, 8, 9, 10, 11, 12;
1, 2, 3, 4, 5, 6]
mh=[5, 6, 3, 4, 1, 2;
11, 12, 9, 10, 7, 8;
17, 18, 15, 16, 13, 14]
mb=[17, 18, 15, 16, 13, 14;
11, 12, 9, 10, 7, 8;
5, 6, 3, 4, 1, 2]
行列要素の最小値・最大値を求める¶
行列要素の最小値・最大値,およびそれの位置を求めます.(例えば,最大値だけが必要で,最小値が不要な場合など)求める必要がないパラメータには NULL を渡すこともできます. また,マスクを利用して,限定された範囲内の最小値・最大値を求めることも可能です.
シングルチャンネル行列の最小値・最大値¶
minMaxLoc に渡せる行列はシングルチャンネルのみです.つまり,1つのチャンネルの最大値のみを求めることができます.しかし,reshape() メソッドを利用することで,すべてのチャンネルの中で最大の値を求めることもできます.
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
// 3x3 の行列
cv::Mat m1 = (cv::Mat_<double>(3,3) << 1, 2, 3, 4, 5, 6, 7, 8, 9);
double minVal, maxVal;
cv::Point minLoc, maxLoc;
cv::minMaxLoc(m1, &minVal, &maxVal, &minLoc, &maxLoc);
std::cout << "m1=" << m1 << std::endl << std::endl;
std::cout << "min=" << minVal << ", " << minLoc << std::endl << std::endl;
std::cout << "max=" << maxVal << ", " << maxLoc << std::endl << std::endl;
// 最小値・最大値が複数あると...
m1.at<double>(0,1) = 1;
m1.at<double>(2,1) = 9;
// 最初に見つかった位置が返される
cv::minMaxLoc(m1, &minVal, &maxVal, &minLoc, &maxLoc);
std::cout << "m1=" << m1 << std::endl << std::endl;
std::cout << "min=" << minVal << ", " << minLoc << std::endl << std::endl;
std::cout << "max=" << maxVal << ", " << maxLoc << std::endl << std::endl;
}
実行結果:
m1=[1, 2, 3;
4, 5, 6;
7, 8, 9]
min=1, [0, 0]
max=9, [2, 2]
m1=[1, 1, 3;
4, 5, 6;
7, 9, 9]
min=1, [0, 0]
max=9, [1, 2]
2次元点集合間の最適なアフィン変換を推定する¶
2つの2次元点集合間の最適な2次元のアフィン変換を推定します. パラメータを指定することにより,並進,回転,等方スケーリングに制限されたアフィン変換(5自由度)を推定することもできます.
2次元のアフィン変換を行う も参照してください.
#include <iostream>
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp> //
#include <opencv2/video/tracking.hpp> // for 2.3 or later
int
main(int argc, char *argv[])
{
cv::Size img_size(500, 500);
cv::Mat img = cv::Mat::zeros(img_size, CV_8UC3);
// 3x3 の行列
int rand_num = 10;
cv::Mat_<float> points(rand_num, 3);
cv::Mat src_points(points, cv::Rect(0,0,2,rand_num));
cv::randu(points, cv::Scalar(100), cv::Scalar(400));
for(int i=0; i<rand_num; ++i) {
points(i, 2) = 1.0;
// 変換前の座標点を描画(水色の点)
cv::circle(img, cv::Point(points(i,0), points(i,1)), 2, cv::Scalar(200,200,0), -1, CV_AA);
}
cv::Mat affine_matrix = (cv::Mat_<float>(2, 3) << 0.7660,-0.8428,214.1616,0.6428,0.9660,-108.4043);
cv::Mat dst_points = points * affine_matrix.t();
// 変換後の座標点を描画(赤色の点)
for(int i=0; i<rand_num; ++i) {
cv::circle(img, cv::Point(dst_points.at<float>(i,0), dst_points.at<float>(i,1)), 2, cv::Scalar(50,50,255), -1, CV_AA);
}
// 2次元アフィン変換の推定(回転,並進,拡大縮小の拘束あり)
cv::Mat est_matrix = cv::estimateRigidTransform(src_points.reshape(2), dst_points.reshape(2), false);
// 2次元アフィン変換の推定(拘束なし)
cv::Mat est_matrix_full = cv::estimateRigidTransform(src_points.reshape(2), dst_points.reshape(2), true);
std::cout << "Affine Transformation Matrix:" << std::endl;
std::cout << affine_matrix << std::endl << std::endl;
std::cout << "Estimated Matrix:" << std::endl;
std::cout << est_matrix << std::endl << std::endl;
std::cout << "Estimated Matrix (full):" << std::endl;
std::cout << est_matrix_full << std::endl << std::endl;
/// 元の点を推定した変換行列で変換する
cv::Mat est_matrixF, est_matrixF_full;
est_matrix.convertTo(est_matrixF, CV_32F);
est_matrix_full.convertTo(est_matrixF_full, CV_32F);
cv::Mat_<float> est_points = points * est_matrixF.t();
cv::Mat_<float> est_points_full = points * est_matrixF_full.t();
for(int i=0; i<rand_num; ++i) {
// 拘束ありのアフィン変換で変換した点集合を描画(緑色の円)
cv::circle(img, cv::Point(est_points(i,0), est_points(i,1)), 5, cv::Scalar(50,255,50), 1, CV_AA);
// 拘束なしのアフィン変換で変換した点集合を描画(黄色の円)
cv::circle(img, cv::Point(est_points_full(i,0), est_points_full(i,1)), 5, cv::Scalar(50,255,255), 1, CV_AA);
}
cv::namedWindow("image", CV_WINDOW_AUTOSIZE|CV_WINDOW_FREERATIO);
cv::imshow("image", img);
cv::waitKey(0);
}
実行結果:
Affine Transformation Matrix:
[0.76599997, -0.84280002, 214.16161;
0.64279997, 0.96600002, -108.4043]
Estimated Matrix:
[0.8995064623862854, -0.8670171167356711, 198.2603717112048;
0.8670171167356711, 0.8995064623862854, -128.2613453078639]
Estimated Matrix (full):
[0.7659999426447789, -0.8428000332703937, 214.1616156934035;
0.6427999985417542, 0.966000008132273, -108.4043013037557]
水色:入力点集合1,赤色:入力点集合2: 集合1から集合2へのアフィン変換を推定します.
緑色の円:制限されたアフィン変換による変換後の点,黄色の円:任意のアフィン変換による変換後の点,

連立1次方程式を解く¶
cv::solve() を利用する場合,右辺,左辺の係数を格納する行列の型は共に,32Fまたは64Fである必要があります.
非特異系¶
独立した方程式の数が変数の数に等しく,行列式がゼロではない場合で,一意な解が存在します.
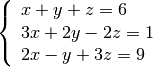
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
// 左辺
cv::Mat lhand = (cv::Mat_<double>(3,3) << 1,1,1,3,2,-2,2,-1,3);
// 右辺
cv::Mat rhand = (cv::Mat_<double>(3,1) << 6,1,9);
// ガウスの消去法により解を求める
cv::Mat ans;
cv::solve(lhand, rhand, ans);
std::cout << "(x,y,z) = " << ans << std::endl;
}
実行結果:
(x,y,z) = [1; 2; 3]
優決定系¶
方程式の数が変数の数より大きい場合で,解は存在しない可能性がありますが,OpenCVでは最小二乗問題を解くことになります.
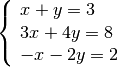
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
// 左辺
cv::Mat lhand = (cv::Mat_<double>(3,2) << 1,1,3,4,-1,-2);
// 右辺
cv::Mat rhand = (cv::Mat_<double>(3,1) << 3,8,2);
// SVDにより最小二乗問題の解を求める
cv::Mat x;
cv::solve(lhand, rhand, x, cv::DECOMP_SVD);
std::cout << "(x,y) = " << x << std::endl;
std::cout << "norm(lhand*x-rhand)=" << norm(lhand*x-rhand) << std::endl;
}
実行結果:
(x,y) = [9.999999999999998; -5.666666666666665]
norm(lhand*x-rhand)=1.63299
特異値分解を行う¶
特異値分解を行います. 特異値分解の実装は,OpenCV-2.3で,Lapackを利用しないものに変更されました. しかし,2.3,2.3.1 では,入力行列 A を直接変更する(ことで,多少の速度向上とメモリ節約が見込まれる)オプションフラグ SVD::MODIFY_A フラグを利用することができません.
#include <iostream>
#include <opencv2/core/core.hpp>
int
main(int argc, char *argv[])
{
// 2x4 の行列
cv::Mat A = (cv::Mat_<double>(2,4) << 1, 2, 3, 4, 5, 6, 7, 8);
std::cout << "A=" << A << std::endl << std::endl;;
// 特異値分解
cv::Mat w, u, vt;
cv::SVD::compute(A, w, u, vt, cv::SVD::FULL_UV);
std::cout << "w=" << w << std::endl;
std::cout << "u=" << u << std::endl;
std::cout << "vt=" << vt << std::endl << std::endl;
// 特異値分解(特異値のみ)
cv::SVD::compute(A, w, u, vt, cv::SVD::NO_UV);
std::cout << "w=" << w << std::endl;
std::cout << "u=" << u << std::endl;
std::cout << "vt=" << vt << std::endl << std::endl;
// SVDクラスのコンストラクタで特異値分解
cv::SVD svd1(A, cv::SVD::FULL_UV);
std::cout << "w=" << svd1.w << std::endl;
std::cout << "u=" << svd1.u << std::endl;
std::cout << "vt=" << svd1.vt << std::endl << std::endl;
// 入力行列Aを直接変更するオプションフラグ "A_MODIFY" も存在するが,
// OpenCV-2.3, 2.3.1 では機能しない.
// cv::SVD::compute(A, w, u, vt, cv::SVD::A_MODIFY);
}
実行結果:
A=[1, 2, 3, 4;
5, 6, 7, 8]
w=[14.22740741263374; 1.25732983537911]
u=[0.3761682344281408, -0.9265513797988838;
0.9265513797988838, 0.3761682344281408]
vt=[0.3520616924890126, 0.4436257825895202, 0.5351898726900277, 0.6267539627905352;
0.7589812676751462, 0.3212415991459323, -0.1164980693832817, -0.5542377379124958;
-0.486602119114998, 0.461395992822191, 0.5370143717006115, -0.5118082454078047;
-0.2514326503714135, 0.6979353392740796, -0.6415727274339188, 0.1950700385312527]
w=[14.22740741263374; 1.25732983537911]
u=[]
vt=[]
w=[14.22740741263374; 1.25732983537911]
u=[0.3761682344281408, -0.9265513797988838;
0.9265513797988838, 0.3761682344281408]
vt=[0.3520616924890126, 0.4436257825895202, 0.5351898726900277, 0.6267539627905352;
0.7589812676751462, 0.3212415991459323, -0.1164980693832817, -0.5542377379124958;
-0.486602119114998, 0.461395992822191, 0.5370143717006115, -0.5118082454078047;
-0.2514326503714135, 0.6979353392740796, -0.6415727274339188, 0.1950700385312527]