画像の幾何学変換¶
このサブセクションで述べる関数は,2次元画像の様々な幾何学変換を行います.つまり,画像の内容は変更せずにピクセルグリッドだけを変形し,変形したグリッドを出力画像にマッピングします.実際には,サンプリングによる余計な値や不定な値を排除するために,出力画像から入力画像という逆方向へのマッピングが行われます.つまり,出力画像の各ピクセル
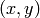 に対して,入力画像中の対応する「ドナー」ピクセルの座標を求め,そのピクセル値をコピーします:
に対して,入力画像中の対応する「ドナー」ピクセルの座標を求め,そのピクセル値をコピーします:
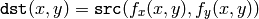
ユーザが正順のマッピング:
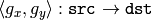 を指定した場合,OpenCV の関数は最初に,対応する逆マッピング:
を指定した場合,OpenCV の関数は最初に,対応する逆マッピング:
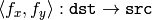 を求めてから上述の式を利用します.
を求めてから上述の式を利用します.
幾何学変換の実際の実装では,最も汎用的な remap() から,最も単純で高速な resize() まで,上述の式を用いて2つの主な問題を解く必要があります:
- 存在しないピクセルの外挿.
と同様に,ある
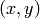 に対して,
に対して,
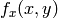 または
または
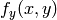 のどちらか,あるいは両方が画像の外側にはみ出してしまう可能性があります.この場合,何らかの外挿手法が必要になります.OpenCVでは,フィルタリング関数の場合と同じく,いくつかの外挿手法が提供されています.さらに別の手法も追加されており,その
BORDER_TRANSPARENT
は,出力画像中の対応するピクセルが全く変更されないことを意味します.
のどちらか,あるいは両方が画像の外側にはみ出してしまう可能性があります.この場合,何らかの外挿手法が必要になります.OpenCVでは,フィルタリング関数の場合と同じく,いくつかの外挿手法が提供されています.さらに別の手法も追加されており,その
BORDER_TRANSPARENT
は,出力画像中の対応するピクセルが全く変更されないことを意味します. - ピクセル値の内挿.通常
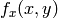 と
と
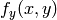 は,浮動小数点数(つまり,
は,浮動小数点数(つまり,
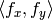 は,アフィン変換,透視変換,または半径方向のレンズ歪み係数など)です.よって,小数点座標上に存在するピクセル値が必要になります.最も単純なケースでは,この座標は単に最も近い整数値の座標に丸められ,そこのピクセル値が利用されます.これは,最近傍補間と呼ばれます.しかし,より洗練された
補間手法
を用いることで,より良い結果が得られます.この場合,求められたピクセル
は,アフィン変換,透視変換,または半径方向のレンズ歪み係数など)です.よって,小数点座標上に存在するピクセル値が必要になります.最も単純なケースでは,この座標は単に最も近い整数値の座標に丸められ,そこのピクセル値が利用されます.これは,最近傍補間と呼ばれます.しかし,より洗練された
補間手法
を用いることで,より良い結果が得られます.この場合,求められたピクセル
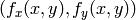 近傍に対して多項式関数をフィッティングし,
近傍に対して多項式関数をフィッティングし,
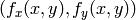 における多項式の値を,補間されたピクセル値として利用します.OpenCVでは,複数の補間手法から選択することができます.詳しくは
resize()
を参照してください.
における多項式の値を,補間されたピクセル値として利用します.OpenCVでは,複数の補間手法から選択することができます.詳しくは
resize()
を参照してください.
cv::GetRotationMatrix2D¶
- GetRotationMatrix2D(center, angle, scale, mapMatrix) → None¶
2次元回転のアフィン変換行列を求めます.
パラメタ: - center (CvPoint2D32f) – 入力画像における回転中心
- angle (float) – 度単位で表される回転角度.正の値は,反時計回りの回転を意味します(座標原点は左上にあると仮定されます)
- scale (float) – 等方性スケーリング係数
- mapMatrix (CvMat) –
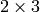 の出力行列へのポインタ
の出力行列へのポインタ
関数 cv2DRotationMatrix は,次のような変換行列を求めます:
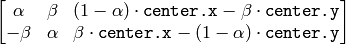
ここで,
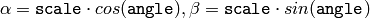
です. この変換は,回転中心をそれ自身に写像します.それを意図していない場合は,並進を調整しなければいけません.
cv::GetAffineTransform¶
- GetAffineTransform(src, dst, mapMatrix) → None¶
3組の対応点を用いてアフィン変換行列を求めます.
パラメタ: - src (CvPoint2D32f) – 入力画像における三角形の3つの頂点座標
- dst (CvPoint2D32f) – 出力画像における,入力画像の3点に対応する3つの頂点座標
- mapMatrix (CvMat) –
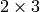 の出力行列へのポインタ
の出力行列へのポインタ
この関数は,次のようなアフィン変換行列を求めます:
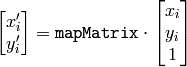
ここで
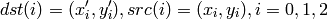
です.
cv::GetPerspectiveTransform¶
- GetPerspectiveTransform(src, dst, mapMatrix) → None¶
3組の対応点を用いて透視変換行列を求めます.
パラメタ: - src (CvPoint2D32f) – 入力画像における四角形の4つの頂点座標
- dst (CvPoint2D32f) – 出力画像における,入力画像の4点に対応する4つの頂点座標
- map_matrix –
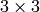 の出力行列へのポインタ
の出力行列へのポインタ
この関数は,次のような透視変換行列を求めます:
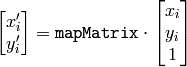
ここで
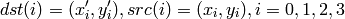
です.
cv::GetQuadrangleSubPix¶
- GetQuadrangleSubPix(src, dst, mapMatrix) → None¶
画像から,四角形領域のピクセル値をサブピクセル精度で取得します.
パラメタ:
この関数は,以下のようにして src からサブピクセル精度でピクセル値を取得し,それを dst に格納します:
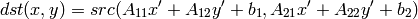
ここで
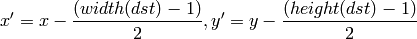
であり,また
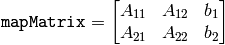
です.
非整数の座標におけるピクセル値は,バイリニア補間を用いて取得されます.画像外部にある領域のピクセル値を取得する場合は,複製境界モードを利用します.また,マルチチャンネル画像の各チャンネルは,それぞれ独立に処理されます.
cv::GetRectSubPix¶
- GetRectSubPix(src, dst, center) → None¶
画像から,矩形領域のピクセル値をサブピクセル精度で取得します.
パラメタ: - src (CvArr) – 入力画像
- dst (CvArr) – 抽出された矩形領域
- center (CvPoint2D32f) – 浮動小数点数で表現された,矩形領域の中心座標.中心座標は,必ず画像内になければいけません
この関数は,以下のように, src からピクセル値を取得します:
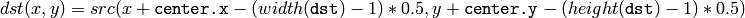
ここで,非整数の座標におけるピクセル値は,バイリニア補間を用いて取得されます.また,マルチチャンネル画像の各チャンネルは,それぞれ独立に処理されます.矩形領域のの中心は,必ず画像内部になければいけませんが,矩形領域の一部が画像外部にはみ出していても構いません.その場合は,画像外部にある領域のピクセル値を取得するために,複製境界モードを利用します.
cv::LogPolar¶
- LogPolar(src, dst, center, M, flags=CV_INNER_LINEAR+CV_WARP_FILL_OUTLIERS) → None¶
画像を対数極座標空間に写像します.
パラメタ: - src (CvArr) – 入力画像
- dst (CvArr) – 出力画像
- center (CvPoint2D32f) – 変換中心.この場所で,出力の精度が最大となります
- M (float) – スケーリング係数の大きさ.以下の説明を参照してください
- flags (int) –
補間手法,および以下に示すオプションフラグの組み合わせ:
- CV_WARP_FILL_OUTLIERS 出力画像の全ピクセルを埋めます.対応するピクセルが入力画像の範囲外であるようなピクセルには,値として 0がセットされます
- CV_WARP_INVERSE_MAP 以下の説明を参照してください
この関数は,入力画像に対して次のような変換を行います:
順変換( CV_WARP_INVERSE_MAP が指定されていない場合 ):
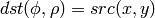
逆変換( CV_WARP_INVERSE_MAP が指定されている場合 ):
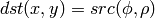
ここで
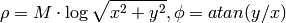
です.
この関数は,人間の「中心」視を模倣したものであり,物体追跡などのための,高速なスケーリングと回転に不変なテンプレートマッチングに利用できます.また,この関数は,置換モードでは動作しないことに注意してください.
cv::Remap¶
- Remap(src, dst, mapx, mapy, flags=CV_INNER_LINEAR+CV_WARP_FILL_OUTLIERS, fillval=(0, 0, 0, 0)) → None¶
画像の幾何学変換を行います.
パラメタ:
この関数は,指定された写像を用いて次のように入力画像を変換します:
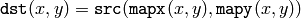
他の幾何変換と同様,非整数の座標におけるピクセル値を求めるために,(ユーザが指定する)補間手法が用いられます.また,この関数は,置換モードでは動作しないことに注意してください.
cv::Resize¶
- Resize(src, dst, interpolation=CV_INTER_LINEAR) → None¶
画像をリサイズします.
パラメタ:
この関数は,画像 src を dst に正確に一致するようにリサイズします.また,ROIが設定されている場合には,それを考慮します.
cv::WarpAffine¶
- WarpAffine(src, dst, mapMatrix, flags=CV_INTER_LINEAR+CV_WARP_FILL_OUTLIERS, fillval=(0, 0, 0, 0)) → None¶
画像のアフィン変換を行います.
パラメタ: - src (CvArr) – 入力画像
- dst (CvArr) – 出力画像
- mapMatrix (CvMat) –
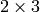 の変換行列
の変換行列 - flags (int) –
補間手法,および以下に示すオプションフラグの組み合わせ:
- CV_WARP_FILL_OUTLIERS 出力画像の全ピクセルを埋めます.対応するピクセルが入力画像の範囲外であるようなピクセルには,値として fillval がセットされます
- CV_WARP_INVERSE_MAP これは, matrix が出力画像から入力画像への逆変換であることを表します.したがって,この行列を直接ピクセル補間に利用できます.このフラグが指定されていない場合は,この関数が mapMatrix の逆変換を求めます
- fillval (CvScalar) – 対応のとれない点を埋める値
この関数は,指定された行列を用いて入力画像を以下のように変換します:
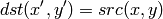
ここで
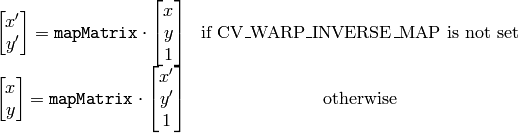
です.
この関数は, GetQuadrangleSubPix と似ていますが,完全に等価というわけではありません WarpAffine は,入力画像と出力画像が同じデータ型でなければならず,オーバーヘッドも大きいです(よって,小さい画像を変換するのには適していません).さらに,出力画像の一部を変更しないままにしておく事もできます.一方, GetQuadrangleSubPix は,8ビット画像から抽出した矩形領域のピクセル値を浮動小数点型のバッファに保存しますし,オーバーヘッドも小さいです.さらに,常に出力画像全体が変更され,すべてのピクセルが埋められます.また,この関数は,置換モードでは動作しないことに注意してください.
疎な点集合を変換する場合は,cxcore の関数 Transform を利用します.
cv::WarpPerspective¶
- WarpPerspective(src, dst, mapMatrix, flags=CV_INNER_LINEAR+CV_WARP_FILL_OUTLIERS, fillval=(0, 0, 0, 0)) → None¶
画像の透視変換を行います.
パラメタ: - src (CvArr) – 入力画像
- dst (CvArr) – 出力画像
- mapMatrix (CvMat) –
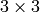 の変換行列
の変換行列 - flags (int) –
補間手法,および以下に示すオプションフラグの組み合わせ:
- CV_WARP_FILL_OUTLIERS 出力画像の全ピクセルを埋める.対応するピクセルが入力画像の範囲外であるようなピクセルには,値として fillval がセットされます
- CV_WARP_INVERSE_MAP これは, matrix が出力画像から入力画像への逆変換であることを表します.したがって,この行列を直接ピクセル補間に利用できます.このフラグが指定されていない場合は,この関数が map_matrix の逆変換を求めます
- fillval (CvScalar) – 対応のとれない点を埋める値
この関数は,指定された行列を用いて入力画像を以下のように変換します:
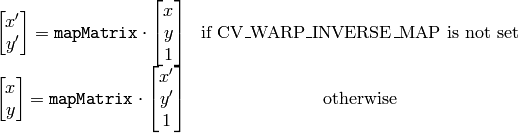
この関数は,置換モードでは動作しないことに注意してください.また,疎な点集合を変換する場合は,cxcore の関数 PerspectiveTransform を利用します.
ヘルプとフィードバック
お探しの情報が見つかりませんか?- FAQ (英語)を試してください.
- ユーザグループ/メーリングリスト (英語)で質問してみてください.
- このドキュメントに誤りなどを見つけたらbug report まで報告してください.また,日本語訳に関する誤りや指摘はopencv.jpまでお願い します.
![[A|b]](_images/math/5811dc4a2ff4e426ab272d1d4da6988db5790e51.png) (以下の説明を参照してください)
(以下の説明を参照してください)