構造解析と形状ディスクリプタ¶
cv::ApproxChains¶
- ApproxChains(src_seq, storage, method=CV_CHAIN_APPROX_SIMPLE, parameter=0, minimal_perimeter=0, recursive=0) → chains¶
フリーマンチェーンを,折れ線で近似します.
パラメタ: - src_seq (CvSeq) – 他のチェーンを参照できるチェーンへのポインタ
- storage (CvMemStorage) – 結果として得られる折れ線を保存するストレージ
- method (int) – 近似手法(関数 FindContours の説明を参照してください)
- parameter (float) – 近似手法のパラメータ(現在は利用されていません)
- minimal_perimeter (int) – minimal_perimeter 以上の周囲長をもつ輪郭のみを近似します.その他のチェーンは,結果の構造体から削除されます
- recursive (int) – これが0ではない場合, src_seq から h_next と v_next links によって辿ることができる全てのチェーンが近似されます.0の場合は,1つのチェーンのみが近似されます
これは,単独動作可能な近似ルーチンです.関数 cvApproxChains は,これに相当する近似フラグを引数として与えた場合の FindContours と全く同じように動作します.この関数は,結果として得られる最初の輪郭へのポインタを返します.もしその他の近似輪郭が存在するならば,返された構造体のフィールド v_next と h_next を辿って取得できます.
cv::ApproxPoly¶
ApproxPoly(src_seq, storage, method, parameter=0, parameter2=0) -> sequence
折れ線(カーブ)を指定された精度で近似します.
param src_seq: 座標点配列のシーケンス param storage: 似された折れ線を保存するストレージ.これがNULLの場合,入力シーケンスのストレージが利用されます param method: 近似手法.Douglas-Peuckerアルゴリズムに相当する CV_POLY_APPROX_DP のみがサポートされます param parameter: 近似手法のパラメータ. CV_POLY_APPROX_DP の場合は,要求する近似精度を意味します param parameter2: src_seq がシーケンスの場合,この値は,1つ のシーケンスを近似するのか, src_seq と同レベル,およびそれより下のレベルに存在する全てのシーケンスを近似するのか,を決定します(階層的輪郭構造体については FindContours の説明を参照してください).また, src_seq が 点座標の配列 CvMat* である場合,この値は折れ線が閉じている( parameter2 !=0 )か,開いている( parameter2 =0 ),を決定します
この関数は,1つあるいは複数の折れ線(カーブ)を近似し,その近似結果を返します.折れ線が複数の場合,結果の木構造は入力のそれと同じ構造になります(1対1に対応します).
cv::ArcLength¶
- ArcLength(curve, slice=CV_WHOLE_SEQ, isClosed=-1) → double¶
輪郭線の周囲長,あるいは曲線の長さを求めます.
パラメタ: - curve (CvArr or CvSeq) – 曲線を表す座標点のシーケンス,または配列
- slice (CvSlice) – 曲線の始点と終点.デフォルトでは,曲線全体の長さが求められます
- isClosed (int) –
閉曲線か否かを表します.以下の3通りが考えられる:
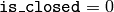 曲線は開いていると見なされます.
曲線は開いていると見なされます.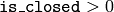 曲線は閉じている見なされます.
曲線は閉じている見なされます.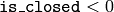 曲線がシーケンスの場合, ((CvSeq*)curve)->flags のフラグが CV_SEQ_FLAG_CLOSED であるか否かによって,曲線が閉じているか否かが決まります.シーケンスではない(頂点の配列 CvMat* で表されている場合)場合は,曲線は開いていると見なされます.
曲線がシーケンスの場合, ((CvSeq*)curve)->flags のフラグが CV_SEQ_FLAG_CLOSED であるか否かによって,曲線が閉じているか否かが決まります.シーケンスではない(頂点の配列 CvMat* で表されている場合)場合は,曲線は開いていると見なされます.
この関数は,曲線上の連続する2点間の線分距離の総和として,曲線の長さを求めます.
cv::BoundingRect¶
- BoundingRect(points, update=0) → CvRect¶
点群を包含する傾いていない矩形を求めます.
パラメタ:
この関数は,2次元点の集合に対する傾いていないバウンディングボックスを返します. 以下に,取り得る points の種類とフラグの組み合わせを示します:
| update | points | action |
|---|---|---|
| 0 | CvContour* | バウンディングボックスを計算せず,輪郭ヘッダのフィールド rect から取得します. |
| 1 | CvContour* | バウンディングボックスを計算し,輪郭ヘッダのフィールド rect に書き込みます. |
| 0 | CvSeq* or CvMat* | バウンディングボックスが計算され,それが返されます. |
| 1 | CvSeq* or CvMat* | ランタイムエラーが発生します. |
cv::BoxPoints¶
- BoxPoints(box) → points¶
箱形状の頂点を求めます.
パラメタ: - box (CvBox2D) – 箱形状
- points (CvPoint2D32f_4) – 頂点の配列
この関数は,入力された2次元の箱形状の頂点を求めます.
cv::CalcPGH¶
- CalcPGH(contour, hist) → None¶
輪郭のペアワイズ幾何ヒストグラムを求めます.
パラメタ: - contour – 入力輪郭.現在は,整数値の座標のみ扱えます
- hist – 計算されたヒストグラム.必ず2次元です
この関数は, Iivarinen97 で提唱された,輪郭に対する2次元のペアワイズ幾何ヒストグラム(PGH)を計算します.このアルゴリズムでは,輪郭を構成する辺同士の全ての組み合わせ(ペア)が考慮されます.各ペアに対して,辺同士が成す角度と,辺同士の最小/最大距離が求められます.そのために,一つ一つの辺を順番に基準辺として,それ以外の辺との関係を全て調べます.基準辺とそれ以外の辺を考える場合,基準辺ではない方の辺上にある点から,基準辺の直線までの最小距離と最大距離が選択されます.この辺同士の角度がヒストグラムの行を定義します.ヒストグラムでは,計算された最小・最大距離の範囲内に含まれる距離に対応する全てのビンが,その値を増加させます(つまり,このヒストグラムは Iivarninen97 での定義に対して,転置されています).このヒストグラムは,輪郭同士のマッチングに利用できます.
cv::CalcEMD2¶
- CalcEMD2(signature1, signature2, distance_type, distance_func = None, cost_matrix=None, flow=None, lower_bound=None, userdata = None) → float¶
2つの重み付き点群間の「最小コスト」距離を求めます.
パラメタ: - signature1 – 1番目のシグネチャ.
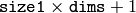 の浮動小数点型行列.各行には点の重みと座標が格納されています.ユーザ定義のコスト関数を使う場合には,この行列は,1列(重みのみ)で構いません
の浮動小数点型行列.各行には点の重みと座標が格納されています.ユーザ定義のコスト関数を使う場合には,この行列は,1列(重みのみ)で構いません - signature2 – 2番目のシグネチャ. signature1 と同じフォーマットですが,行数は異なる可能性があります.重みの総和が異なる場合は, signature1 か signature2 のどちらかに「ダミー」の点が追加されます
- distance_type – 用いられる距離の種類. CV_DIST_L1, CV_DIST_L2 , および CV_DIST_C はそれぞれ,標準的な距離を表しています. CV_DIST_USER の場合は,ユーザ定義関数 distance_func ,あるいは事前に計算された cost_matrix が利用されます
- distance_func –
ユーザ定義の距離関数.2点 pt0 と pt1 を引数にとり,その間の距離を返します ``
func(pt0, pt1, userdata) -> float``
- cost_matrix – ユーザ定義の
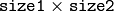 のコスト行列.少なくとも, cost_matrix と distance_func のどちらかは NULL でなければいけません.また,コスト行列が利用される場合は,距離関数を必要とする下限値(下記の説明を参照してください)の計算はできません
のコスト行列.少なくとも, cost_matrix と distance_func のどちらかは NULL でなければいけません.また,コスト行列が利用される場合は,距離関数を必要とする下限値(下記の説明を参照してください)の計算はできません - flow – 結果として得られる
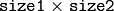 のフロー行列:
のフロー行列: 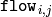 は, signature1 の
は, signature1 の 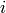 番目の点から signature2 の
番目の点から signature2 の 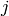 番目の点までのフローを表します
番目の点までのフローを表します - lower_bound – オプションである入出力パラメータ.2つのシグネチャ間の距離,つまりそれぞれの重心間同士の距離の下限値.ユーザ定義のコスト行列を利用する場合,互いの点群の重みの総和が等しくない場合,シグネチャが重みのみで構成されている場合(つまり,シグネチャが1行の行列の場合)は,この下限値は計算されません.ユーザは, 必ず *lower_bound を初期化しなければいけません.また,計算された重心間距離が *lower_bound 以上だった場合(これは,シグネチャ同士が十分に離れている事を意味します),この関数はEMDの計算を行いません.したがって,重心間距離とEMDの両方を求めたい場合は, *lower_bound を0にセットするべきです
- userdata – オプション.ユーザ定義の距離関数に渡されるデータへのポインタ
- signature1 – 1番目のシグネチャ.
この関数は,EMDと2つの重み付き点群間の距離の下限値のどちらか片方,あるいは両方を計算します.これの RubnerSept98 で述べられている応用例の1つが,画像抽出のための多次元ヒストグラム比較です.EMDは,修正シンプレックス法で解くことができる輸送問題なので,最悪の場合は計算量が指数関数的に増加するが,平均的には十分高速に計算できます.実際は,(線形時間アルゴリズムを利用して)下限値をより高速に求めることが可能で,2つのシグネチャが十分に離れており,同一物体に関連するものではないと判断するのに利用できます.
cv::CheckContourConvexity¶
- CheckContourConvexity(contour) → int¶
輪郭形状が凸であるかを調べます.
Parameter: contour (CvArr or CvSeq) – 対象となる輪郭(座標点のシーケンス,または配列)
この関数は,入力輪郭が凸であるか否かを調べます.この輪郭は,自己交差しないような単純なものでなければいけません.
CvConvexityDefect¶
- class CvConvexityDefect¶
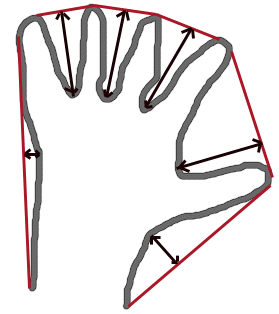
タプル (start, end, depthpoint, depth) で表現される,一つの輪郭凹状欠損.
- start¶
- 輪郭の凹状欠損の始点 (x, y)
- end¶
- 輪郭の凹状欠損の終点 (x, y)
- depthpoint¶
- 凹状欠損の中で凸包から最も遠い点 (x, y)
- depth¶
- 最も遠い点と凸包間の距離
cv::ContourArea¶
- ContourArea(contour, slice=CV_WHOLE_SEQ) → double¶
全輪郭,あるい輪郭の一部が囲む領域面積を求めます.
パラメタ:
この関数は,全輪郭,あるい輪郭の一部が囲む領域面積を求めます.後者の場合,以下の図のように,輪郭の弧と2点を結ぶ弦によって区切られた総面積が求められます:
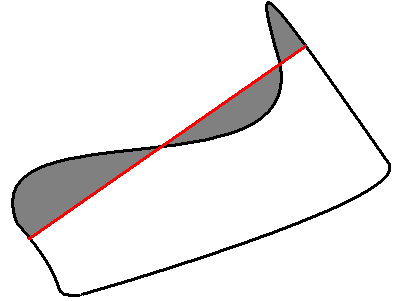
輪郭の姿勢によっては, 負の 値を返すことがあります.面積の絶対値を得るには,C言語の fabs() を利用してください.
cv::ContourFromContourTree¶
- ContourFromContourTree(tree, storage, criteria) → contour¶
木構造から輪郭を復元します.
パラメタ: - tree (CvContourTree) – 輪郭を表す木
- storage (CvMemStorage) – 復元された輪郭を保存するストレージ
- criteria (CvTermCriteria) – 復元を停止するための停止基準
この関数は,その二分木表現から輪郭を復元します.パラメータ criteria は,精度と復元に利用する木のレベル数のどちらか片方,あるいは両方を決めます.これにより,近似された輪郭を作成することができます.また,この関数は,復元された輪郭を返します.
cv::ConvexHull2¶
- ConvexHull2(points, storage, orientation=CV_CLOCKWISE, return_points=0) → convex_hull¶
点集合に対する凸包を求めます.
パラメタ: - points (CvArr or CvSeq) – 2次元点,あるいは3次元点のシーケンス,または配列.要素は,32ビット整数型,あるいは浮動小数点型の座標
- storage (CvMemStorage) – 凸包を保存するための出力配列(CvMat*),あるいはメモリストレージ(CvMemStorage*).配列の場合,入力配列/シーケンスと同数の要素をもつ1次元配列でなければいけません.また出力時には,配列を凸包のサイズまで切り詰めるようにヘッダが変更されます. hull_storage がNULLの場合,凸包は入力シーケンスと同じストレージに保存されます
- orientation (int) – 凸包を構成するデータの整列方向: CV_CLOCKWISE または CV_COUNTER_CLOCKWISE
- return_points (int) – これが0ならば, storage が配列の場合はインデックスが保存され, storage がメモリストレージの場合はポインタが保存されます.0以外ならば,凸包を構成する点自身が保存されます
この関数は,Sklanskyのアルゴリズムを用いて2次元点集合の凸包を求めます. storage がメモリストレージならば,この関数は,凸包を構成する点,あるいはその点へのポインタを含むシーケンスを作成します.これは return_points の値によって決まり,出力としてこのシーケンスが返されます. storage が CvMat ならば,この関数はNULLを返します.
cv::ConvexityDefects¶
- ConvexityDefects(contour, convexhull, storage) → convexity_defects¶
輪郭の凹状欠損を見つけます.
パラメタ: - contour (CvArr or CvSeq) – 入力輪郭
- convexhull (CvSeq) – ConvexHull2 によって得られる凸包.これは,凸包を構成する点自身ではなく,輪郭点へのポインタあるいはインデックスを持ちます(関数 ConvexHull2 のパラメータ return_points が0でなければいけません)
- storage (CvMemStorage) – 凹状欠損の出力シーケンスを保存するストレージ.これがNULLの場合,輪郭あるいは凸包のストレージが(この優先順位で)使われます
この関数は,入力輪郭の全ての凹状欠損を見つけて,構造体 CvConvexityDefect のシーケンスを返します.
cv::CreateContourTree¶
- CreateContourTree(contour, storage, threshold) → contour_tree¶
輪郭の階層表現を作成します.
パラメタ: - contour (CvSeq) – 入力輪郭
- storage (CvMemStorage) – 出力木構造を保存するストレージ
- threshold (float) – 近似精度
この関数は,入力輪郭 contour の二分木表現を作成し,その根へのポインタを返します.パラメータ threshold が0以下の場合,この関数は全二分木表現を作成します.また,0よりも大きい場合は,精度 threshold の表現を作成します:これは,近似線によって切り取られる元輪郭線上の頂点数が threshold よりも少なくなると,それ以上木を作成しません.また,この関数は,作成された木構造を返します.
cv::FindContours¶
- FindContours(image, storage, mode=CV_RETR_LIST, method=CV_CHAIN_APPROX_SIMPLE, offset=(0, 0)) → cvseq¶
2値画像中の輪郭を抽出します.
パラメタ: - image – 入力画像,8ビット,シングルチャンネル.0以外のピクセルは 1として,0のピクセルは0のまま処理されます.つまり,入力画像は 2値画像 として扱われます.グレースケールから,このような2値画像を得るには, Threshold , AdaptiveThreshold あるいは Canny などの関数を利用します.また,この関数は,入力画像の中身を書き換えます
- storage – 抽出された輪郭を格納するストレージ
- mode –
輪郭抽出モード
- CV_RETR_EXTERNAL 最も外側の輪郭のみを抽出します
- CV_RETR_LIST すべての輪郭を抽出し,それらをリストに保存します
- CV_RETR_CCOMP すべての輪郭を抽出し,をれらを2階層構造として保存します:上のレベルには,連結成分の外側の境界線が,下のレベルには,連結成分の内側に存在する穴の境界線が属します
- CV_RETR_TREE すべての輪郭を抽出し,入れ子構造になった輪郭を完全に表現する階層構造を構成します
- method –
近似手法( CV_LINK_RUNS 以外の全ての手法では,組み込みの近似手法を利用しています)
- CV_CHAIN_CODE 出力はフリーマンチェーンコード. 他の手法では,ポリゴン(頂点のシーケンス)を出力します
- CV_CHAIN_APPROX_NONE チェーンコードの全ての点を,通常の点群に変換します
- CV_CHAIN_APPROX_SIMPLE 水平・垂直・斜めの線分を圧縮し,それらの端点のみを残します
- CV_CHAIN_APPROX_TC89_L1,CV_CHAIN_APPROX_TC89_KCOS Teh-Chin チェーン近似アルゴリズムの1つを適用します
- CV_LINK_RUNS 値が1のセグメントを水平方向に接続する,全く異なる輪郭抽出アルゴリズム.この手法を用いる場合は,抽出モードが CV_RETR_LIST でなければいけません
- offset – オフセット.各輪郭はこの値ぶんだけ平行移動します.これは,ROIの中で抽出された輪郭を,画像全体に対して位置づけて解析する場合に役立ちます
この関数は, Suzuki85 のアルゴリズムを用いて,2値画像から輪郭を抽出します.その輪郭は,形状解析や物体検出,物体認識に役立ちます.
この関数は,2値画像から輪郭を抽出し,その輪郭数を返します.また,ポインタ first_contour に,結果が出力されます.これは,最も外側にある最初の輪郭へのポインタを表し,輪郭が全く抽出されなかった場合(画像が完全に真っ黒の場合)は,戻り値が NULL になります.それ以外の輪郭へは,リンクである h_next と v_next を利用して, first_contour から辿ることができます.関数 DrawContours の説明にあるサンプルは,輪郭を利用して連結成分を抽出する方法について述べています.輪郭は,形状解析や物体認識などにも用いられます - OpenCVサンプルディレクトリにある
squares.py を参照してください.
注意: 元の image は,この関数によって書き換えられます.
cv::FitEllipse2¶
この関数は,2次元点の集合に最もフィットする(二乗誤差が最小になる)楕円を求めます.返される構造体のフィールドは, size が,楕円軸の半分の長さではなく全長を表していることを除けば, Ellipse のそれと同様です..
cv::FitLine¶
- FitLine(points, dist_type, param, reps, aeps) → line¶
2次元あるいは3次元の点集合に直線をフィッティングします.
パラメタ: - points – 2次元点,あるいは3次元点のシーケンス,または配列.要素は,32ビット整数型,あるいは浮動小数点型の座標です
- dist_type – フィッティングに利用される距離(説明を参照してください)
- param – いくつかの距離で利用される数値パラメータ( C ).これが0の場合,最適な値が選択されます
- reps – 半径(座標原点と直線との距離)に対する精度.デフォルト値の0.01 は,適切な値です
- aeps – 角度に対する精度.デフォルト値の0.01 は,適切な値です
- line – 出力直線パラメータ. 2次元フィッティングの場合,これは,4つの浮動小数点数 (vx, vy, x0, y0) の タプル となります.ここで, (vx, vy) は直線に乗るように正規化された方向ベクトル, (x0, y0) は直線上の点を表します.3次元フィッティングの場合,これは,6つの浮動小数点数 (vx, vy, vz, x0, y0, z0) の タプル となります.またここで, (vx, vy, vz) は直線に乗るように正規化された方向ベクトル, (x0, y0, z0) は直線上の点を表します
この関数は,
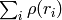 を最小化することで,2次元あるいは3次元の点集合に直線をフィッティングします.ここで,
を最小化することで,2次元あるいは3次元の点集合に直線をフィッティングします.ここで,
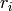 は
は
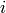 番目の点と直線の距離,
番目の点と直線の距離,
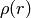 は距離関数(以下の内の1つ)を表します:
は距離関数(以下の内の1つ)を表します:
dist_type=CV_DIST_L2
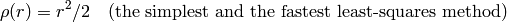
dist_type=CV_DIST_L1
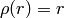
dist_type=CV_DIST_L12
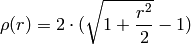
dist_type=CV_DIST_FAIR
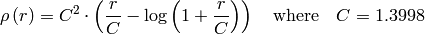
dist_type=CV_DIST_WELSCH
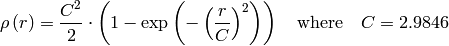
dist_type=CV_DIST_HUBER
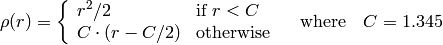
cv::GetCentralMoment¶
- GetCentralMoment(moments, x_order, y_order) → double¶
画像モーメント構造体から,中心モーメントを取得します.
パラメタ: - moments (CvMoments) – 画像モーメント構造体へのポインタ
- x_order (int) – 取得するモーメントのx方向の次数,
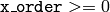
- y_order (int) – 取得するモーメントのy方向の次数,
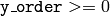 および
および 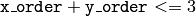
この関数は,中心モーメント,つまり,画像モーメントの場合は次のように定義される値,を取り出します:
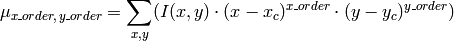
ここで,
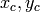 は重心の座標です:
は重心の座標です:
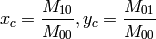
cv::GetHuMoments¶
- GetHuMoments(moments) → hu¶
7つの Hu モーメント不変量を求めます.
パラメタ: - moments – Moments で求められた入力モーメント
- hu – 出力される Hu モーメント不変量
この関数は,次のように定義される 7つの Hu モーメント不変量を求めます. http://en.wikipedia.org/wiki/Image_moment も参照してください.
![\begin{array}{l} hu_1= \eta _{20}+ \eta _{02} \\ hu_2=( \eta _{20}- \eta _{02})^{2}+4 \eta _{11}^{2} \\ hu_3=( \eta _{30}-3 \eta _{12})^{2}+ (3 \eta _{21}- \eta _{03})^{2} \\ hu_4=( \eta _{30}+ \eta _{12})^{2}+ ( \eta _{21}+ \eta _{03})^{2} \\ hu_5=( \eta _{30}-3 \eta _{12})( \eta _{30}+ \eta _{12})[( \eta _{30}+ \eta _{12})^{2}-3( \eta _{21}+ \eta _{03})^{2}]+(3 \eta _{21}- \eta _{03})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}] \\ hu_6=( \eta _{20}- \eta _{02})[( \eta _{30}+ \eta _{12})^{2}- ( \eta _{21}+ \eta _{03})^{2}]+4 \eta _{11}( \eta _{30}+ \eta _{12})( \eta _{21}+ \eta _{03}) \\ hu_7=(3 \eta _{21}- \eta _{03})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}]-( \eta _{30}-3 \eta _{12})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}] \\ \end{array}](_images/math/c0225e5b813ed803409286b71268108e4cceda75.png)
ここで
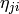 は,正規化された中心モーメントを表します.
は,正規化された中心モーメントを表します.
反転によって符号が逆転してしまう7番目のHuモーメントを除いて,これらの値は,画像のスケール変化,回転,および反転に対して不変であることが分かっています.この不変量は,もちろん画像解像度が有限であるという仮定の元に成り立っています.ラスタ画像の場合は,元画像に対する Hu 不変量と変形した画像に対するものとは多少異なります.
>>> import cv
>>> original = cv.LoadImageM("building.jpg", cv.CV_LOAD_IMAGE_GRAYSCALE)
>>> print cv.GetHuMoments(cv.Moments(original))
(0.0010620951868446141, 1.7962726159653835e-07, 1.4932744974469421e-11, 4.4832441315737963e-12, -1.0819359198251739e-23, -9.5726503811945833e-16, -3.5050592804744648e-23)
>>> flipped = cv.CloneMat(original)
>>> cv.Flip(original, flipped)
>>> print cv.GetHuMoments(cv.Moments(flipped))
(0.0010620951868446141, 1.796272615965384e-07, 1.4932744974469935e-11, 4.4832441315740249e-12, -1.0819359198259393e-23, -9.572650381193327e-16, 3.5050592804745877e-23)
cv::GetNormalizedCentralMoment¶
- GetNormalizedCentralMoment(moments, x_order, y_order) → double¶
画像モーメント構造体から,正規化された中心モーメントを取得します.
パラメタ: - moments (CvMoments) – 画像モーメント構造体へのポインタ
- x_order (int) – 取得するモーメントのx方向の次数,
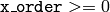
- y_order (int) – 取得するモーメントのy方向の次数,
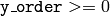 および
および 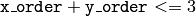
この関数は, 次のように正規化された中心モーメントを取得します:
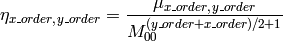
cv::GetSpatialMoment¶
- GetSpatialMoment(moments, x_order, y_order) → double¶
画像モーメント構造体から,空間モーメントを取得します.
パラメタ: - moments (CvMoments) – Moments によって計算される画像モーメント構造体へのポインタ
- x_order (int) – 取得するモーメントのx方向の次数,
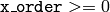
- y_order (int) – 取得するモーメントのy方向の次数,
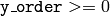 および
および 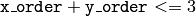
この関数は,空間モーメント,つまり,画像モーメントの場合は次のように定義される値,を取り出します:
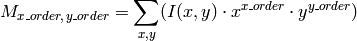
ここで,
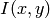 は,ピクセル
は,ピクセル
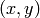 の輝度値です.
の輝度値です.
cv::MatchContourTrees¶
- MatchContourTrees(tree1, tree2, method, threshold) → double¶
2つの輪郭を,その二分木表現によって比較します.
パラメタ: - tree1 (CvContourTree) – 1番目の木表現
- tree2 (CvContourTree) – 2番目の木表現
- method (int) – 類似度. CV_CONTOUR_TREES_MATCH_I1 のみをサポートします
- threshold (float) – 類似度の閾値
この関数は,2つの輪郭(木)の類似度を求めます.この類似度は,二分木の根から順に,それぞれのレベル毎に計算されます.あるレベルにおいて,輪郭間の差が threshold よりも小さくなった場合,復元処理が中断され,その時点での差が返されます.
cv::MatchShapes¶
- MatchShapes(object1, object2, method, parameter=0) → None¶
2つの形状を比較します.
パラメタ:
この関数は,2つの形状を比較します.実装されている3つの手法は,いずれもHuモーメント(
GetHuMoments
の説明を参照してください)を利用します(
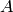 は
object1
,
は
object1
,
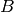 は
object2
を表します):
は
object2
を表します):
method=CV_CONTOUR_MATCH_I1
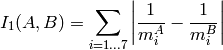
method=CV_CONTOUR_MATCH_I2
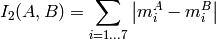
method=CV_CONTOUR_MATCH_I3
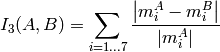
ここで,
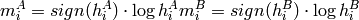
です.
また,
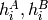 は,
は,
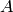 と
と
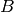 それぞれのHuモーメントを表します.
それぞれのHuモーメントを表します.
cv::MinAreaRect2¶
- MinAreaRect2(points, storage=NULL) → CvBox2D¶
与えられた2次元点集合を囲む最小の矩形を求めます.
パラメタ: - points (CvArr or CvSeq) – 座標点のシーケンス,あるいは配列
- storage (CvMemStorage) – オプション.一時的に使用されるメモリストレージ
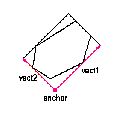
この関数は,点集合に対する凸包を作成し,その凸包に対して rotating calipers 法を適用することにより,与えられた2次元点集合を囲む最小の矩形を求めます.
図.輪郭を囲む最小面積の矩形
cv::MinEnclosingCircle¶
- MinEnclosingCircle(points)-> (int, center, radius)¶
与えられた2次元点集合を囲む最小の円を求めます.
パラメタ: - points (CvArr or CvSeq) – 座標点のシーケンス,あるいは配列
- center (CvPoint2D32f) – 出力パラメータ.包含円の中心座標
- radius (float) – 出力パラメータ.包含円の半径
この関数は,反復アルゴリズムを用いて,与えられた2次元点集合を囲む最小の円を求めます.そして,結果として得られる円が全ての入力点を囲んでいる場合は0以外の値を返し,そうでない場合(つまり,アルゴリズムが失敗した場合)は0を返します.
cv::Moments¶
- Moments(arr, binary = 0) → moments¶
ポリゴンあるいはラスタライズされた形状の,3次までのモーメントを求めます.
パラメタ:
この関数は,3次までの空間モーメントあるいは中心モーメントを計算し,それらを moments に書き込みます.そしてこれらのモーメントは,形状の重心,面積,主軸,そして7つのHuモーメント不変量を含む各種の形状特徴を計算するために利用されます.
cv::PointPolygonTest¶
- PointPolygonTest(contour, pt, measure_dist) → double¶
点と輪郭の位置関係を調べます.
パラメタ: - contour (CvArr or CvSeq) – 入力輪郭
- pt (CvPoint2D32f) – 輪郭との位置関係を調べる座標点
- measure_dist (int) – これが0以外ならば,この関数は点からそれに最も近い輪郭の辺までの距離を推定します
この関数は,与えられた点が輪郭の内側,外側,あるいは輪郭の辺上(あるいは,頂点上)のどこにあるかを判定します.そして,その結果に応じて,正,負,0のいずれかの値が返されます.
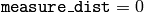 の場合,戻り値はそれぞれ +1,-1,0です.また,
の場合,戻り値はそれぞれ +1,-1,0です.また,
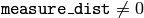 の場合,入力点とそれに最も近い輪郭の辺までの符号付き距離が返されます.
の場合,入力点とそれに最も近い輪郭の辺までの符号付き距離が返されます.
ここでは,この関数の出力例として,各画像ピクセルが輪郭に対してテストされる様子を示します.

ヘルプとフィードバック
お探しの情報が見つかりませんか?- FAQ (英語)を試してください.
- ユーザグループ/メーリングリスト (英語)で質問してみてください.
- このドキュメントに誤りなどを見つけたらbug report まで報告してください.また,日本語訳に関する誤りや指摘はopencv.jpまでお願い します.
