平面細分割¶
CvSubdiv2D¶
- class CvSubdiv2D¶
平面細分割.
平面細分割とは,重複しない小領域(細分割面)で全平面を細分化することです.上記の構造体は 2 次元の点集合によって細分割を表現しており,その点集合の点は互いに連結され,平面グラフを構成します.このグラフは,無限遠にある外部細分割点(通常は,凸包点)と接続する少数の辺をもち,その辺によって平面を小領域に分割していきます.
すべての細分割に対して,その面と点(細分割頂点)の役割を入れ替えた双対細分割が存在します.つまり,双対細分割では,面は頂点として扱われ(以降は,仮想点と呼びます),元の細分割の頂点は面として扱われます.以下の図では,元の細分割が実線で,双対細分割が点線で表されています.
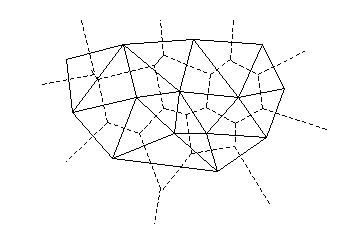
OpenCV では,ドロネーのアルゴリズムを用いて平面を三角形に細分化します.細分割は,確実にすべての細分点を含む仮想の三角形から開始される反復計算により行われます.この場合,双対細分割は入力 2 次元点集合に対するボロノイ図となります.この細分割は,平面の 3 次元区分変換やモーフィング,平面上の点の高速な位置同定,特殊なグラフ(NNGやRNG)の生成などに利用できます.
CvSubdiv2DPoint¶
- class CvSubdiv2DPoint¶
細分割または双対細分割における頂点.
- first¶
接続される CvSubdiv2DEdge .
- pt¶
位置, CvPoint2D32f .
CalcSubdivVoronoi2D¶
- CalcSubdivVoronoi2D(subdiv) → None¶
ボロノイ図のセルの座標を求めます.
パラメタ: subdiv (CvSubdiv2D) – 既にすべての点を含む,ドロネー細分割.
この関数は,仮想点の座標を計算します.元の細分割の頂点に対応するすべての仮想点は,(互いに接続され)その点におけるボロノイ図のセルの境界を形成します.
ClearSubdivVoronoi2D¶
- ClearSubdivVoronoi2D(subdiv) → None¶
すべての仮想点を削除します.
パラメタ: subdiv (CvSubdiv2D) – ドロネー細分割.
この関数は,すべての仮想点を削除します.前回の関数呼び出し後に,細分割が変更されていた場合に,関数 CalcSubdivVoronoi2D の内部で呼ばれます.
CreateSubdivDelaunay2D¶
- CreateSubdivDelaunay2D(rect, storage) → delaunay_triangulation¶
空のドロネー三角形を作成します.
パラメタ: - rect (CvRect) – 細分割に追加されるすべての 2 次元点を含む矩形.
- storage (CvMemStorage) – 細分割結果を保存するストレージ.
この関数は,空のドロネー細分割を作成します.ここに 2 次元点を追加するには,関数 SubdivDelaunay2DInsert を利用します.追加されるすべての点は,引数で指定された矩形内に存在しなければならず,そうでない場合はランタイムエラーが発生します.
三角形分割の結果として,与えられた矩形を覆う 1 つの大きな三角形が作成されることに注意してください.したがって,この三角形の3つの頂点は rect の外側に存在します.
FindNearestPoint2D¶
- FindNearestPoint2D(subdiv, pt) → point¶
与えられた点に最も近い細分割の頂点を求めます.
パラメタ: - subdiv (CvSubdiv2D) – ドロネー細分割,あるいはその他の細分割.
- pt (CvPoint2D32f) – 入力座標点.
この関数は,入力点が細分割内のどこに位置するかを求める,もう1つの関数です.これは,入力点にもっとも近い細分割の頂点を見つけます.入力点を含む分割面は(関数 Subdiv2DLocate によって求められ)開始点として利用されますが,その分割面の頂点が最も近い頂点とは限りません.この関数は,見つかった細分割頂点へのポインタを返します.
Subdiv2DEdgeDst¶
- Subdiv2DEdgeDst(edge) → point¶
辺の終点を返します.
パラメタ: edge (CvSubdiv2DEdge) – 細分割の辺(quad-edgeではありません).
この関数は,辺の終点を返します.入力辺が双対細分割のものであり,仮想点の座標がまだ計算されていない場合,戻り値であるポインタは NULL になる場合があります.この仮想点は,関数 CalcSubdivVoronoi2D を用いて計算することが可能です.
Subdiv2DGetEdge¶
- Subdiv2DGetEdge(edge, type) → CvSubdiv2DEdge¶
与えられた辺に関連する辺の1つを返します.
パラメタ: - edge (CvSubdiv2DEdge) – 細分割の辺(quad-edgeではありません).
- type – 関連する辺の内,どの辺を返すかの指定.以下の中から1つが指定されます:
この関数は,入力辺に関連する辺の1つを返します.
Subdiv2DNextEdge¶
- Subdiv2DNextEdge(edge) → CvSubdiv2DEdge¶
入力辺の始点からみて,入力辺の次にある辺を返します.
パラメタ: edge (CvSubdiv2DEdge) – 細分割の辺(quad-edgeではありません).

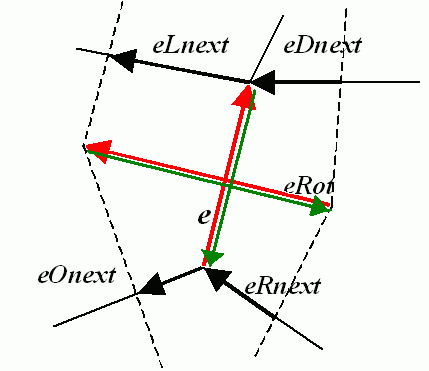
この関数は,入力辺の始点からみて,入力辺の次にある辺を返します:上図の e が入力辺だとすると, eOnext が返されます.
Subdiv2DLocate¶
- Subdiv2DLocate(subdiv, pt) -> (loc, where)¶
ドロネーの三角形内に存在する点の位置を返します.
パラメタ: - subdiv (CvSubdiv2D) – ドロネー細分割,あるいはその他の細分割.
- pt (CvPoint2D32f) – 位置を知りたい点.
- loc (int) – 入力点の,三角分割内における位置.
- where (CvSubdiv2DEdge, CvSubdiv2DPoint) – 辺または頂点.以下の説明を参照してください.
この関数は,入力点が細分割においてどこに位置するかを求めます.ここでは,5つのケースが考えられます:
- 入力点は,分割面内に位置します. loc は CV_PTLOC_INSIDE となり, where はその分割面の辺の1つになります.
- 入力点は,分割辺上に位置します. loc は CV_PTLOC_ON_EDGE となり, where はその辺になります.
- 入力点は,細分割頂点の1つと同じ座標に位置します. loc は CV_PTLOC_VERTEX となり, where はその頂点になります.
- 入力点は,細分割の参照矩形の外側に位置します. loc は CV_PTLOC_OUTSIDE_RECT となり, where は None になります.
- 引数のいずれかが無効.この関数は例外を発生させます.
Subdiv2DRotateEdge¶
- Subdiv2DRotateEdge(edge, rotate) → CvSubdiv2DEdge¶
同じ quad-edge にある別の辺を返します.
パラメタ: - edge (CvSubdiv2DEdge) – 細分割の辺(quad-edgeではありません).
- rotate (int) –
同じquad-edgeにある辺の内,どの辺を返すかの指定.以下の中から1つが指定されます:
- 0 入力辺(下図で e を入力辺とした場合の e 自身).
- 1 回転した辺(下図で e を入力辺とした場合の eRot ).
- 2 反転した辺(下図で e を入力辺とした場合の e を反転した(緑で表現された)辺).
- 3 回転した辺をさらに反転した辺(下図で e を入力辺とした場合の eRot を反転した(緑で表現された)辺).

この関数は,入力辺と同じquad-edgeにある別の辺を返します.
SubdivDelaunay2DInsert¶
- SubdivDelaunay2DInsert(subdiv, pt) → point¶
ドロネーの三角形に1つの点を追加します.
パラメタ: - subdiv (CvSubdiv2D) – 関数 CreateSubdivDelaunay2D によって作成されたドロネー細分割.
- pt (CvPoint2D32f) – 追加される座標点.
この関数は,細分割結果に 1 つの点を追加し,細分割のトポロジーを適切に変更します.もし,既に同じ座標に点が存在していた場合は,点の新規追加は行われません.この関数は,メモリ確保した追加点へのポインタを返します. この段階では,仮想点座標の計算は行われません.
ヘルプとフィードバック
お探しの情報が見つかりませんか?- クックブック を読んでみてみてください.
- ユーザグループ/メーリングリスト (英語)で質問してみてください.
- このドキュメントに誤りなどを見つけたらbug report まで報告してください.また,日本語訳に関する誤りや指摘はOpenCV.jpまでお願いします.
