モーション解析と物体追跡¶
CalcGlobalOrientation¶
- double cvCalcGlobalOrientation(const CvArr* orientation, const CvArr* mask, const CvArr* mhi, double timestamp, double duration)¶
複数の選択領域の全体的なモーション方向を求めます.
パラメタ: - orientation – モーション勾配方向画像.関数 CalcMotionGradient によって計算されます.
- mask – マスク画像. CalcMotionGradient で求められた有効勾配のマスクと,方向を計算する必要がある領域を示すマスクの論理積.
- mhi – モーション履歴画像.
- timestamp – ミリ秒単位,あるいは別の単位で表される現在時間.大きな画像に対して UpdateMotionHistory や CalcMotionGradient を実行すると時間がかかる可能性があるので,事前に UpdateMotionHistory に渡す時間値を保存しておき,ここでそれを再利用する方が良いでしょう.
- duration – ミリ秒単位で表される,モーションの最大持続時間. UpdateMotionHistory のものと同じです.
この関数は,選択領域における全体的なモーション方向を求め,0から360度の間の角度を返します.これはまず,方向ヒストグラムを作成し,ヒストグラムが最大値を取る方向を基本方向とします.次に,全方向ベクトル(相対角度)の重み付き和を求め,基本方向からのズレを計算します:最近の動作ベクトルであるほど,より大きな重みを持ちます.結果として得られる角度は,基本方向とこのズレ量の和になります.
CalcMotionGradient¶
- void cvCalcMotionGradient(const CvArr* mhi, CvArr* mask, CvArr* orientation, double delta1, double delta2, int apertureSize=3)¶
モーション履歴画像の勾配方向を求めます.
パラメタ: - mhi – モーション履歴画像.
- mask – マスク画像.モーション勾配データが有効なピクセルがマークされます.出力パラメータです.
- orientation – モーション勾配方向画像.0~360 度の角度.
- delta1 – 以下を参照してください.
- delta2 – 以下を参照してください.
- apertureSize – この関数で利用される微分オペレータのアパーチャサイズ:CV _ SCHARR, 1, 3, 5, 7( Sobel を参照してください).
この関数は,
mhi
の微分
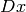 と
と
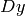 を求め,勾配方向を次のように計算します:
を求め,勾配方向を次のように計算します:
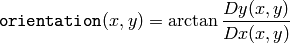
ここでは,(関数
CartToPolar
と同様に)
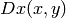 と
と
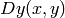 の両方の符号が考慮されます.その後,勾配方向が有効である箇所を示すために
mask
が埋められます.
の両方の符号が考慮されます.その後,勾配方向が有効である箇所を示すために
mask
が埋められます.
この関数は,各ピクセル
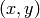 の近傍において,最小(
の近傍において,最小(
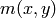 ) と最大(
) と最大(
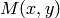 )の mhi 値を求め,以下の条件を満たす場合のみ有効な勾配であるとします.
)の mhi 値を求め,以下の条件を満たす場合のみ有効な勾配であるとします.
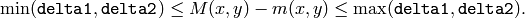
CalcOpticalFlowBM¶
- void cvCalcOpticalFlowBM(const CvArr* prev, const CvArr* curr, CvSize blockSize, CvSize shiftSize, CvSize max_range, int usePrevious, CvArr* velx, CvArr* vely)¶
ブロックマッチング法を用いて,2つの画像に対するオプティカルフローを求めます.
パラメタ: - prev – 1番目の画像.8ビット,シングルチャンネル.
- curr – 2番目の画像.8ビット,シングルチャンネル.
- blockSize – 比較される基本ブロックのサイズ.
- shiftSize – ブロック座標の増加量.
- max_range – ピクセル単位で表される,ブロック周辺の探索範囲サイズ.
- usePrevious – 前回のフレームの速度場を,今回の計算の初期値として利用します.
- velx –
オプティカルフローの水平成分.32ビット,浮動小数点型,シングルチャンネルで,サイズは次のようになります.
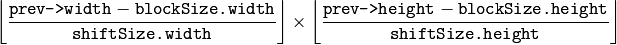
- vely – オプティカルフローの垂直成分. velx と同じサイズ,32ビット,浮動小数点型,シングルチャンネル.
この関数は,重なり合った
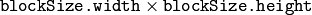 ピクセルのブロック毎にオプティカルフローを計算します.したがって,速度場のサイズは元の画像よりも小さくなります.この関数は,
prev
の各ブロックに対して,
curr
からそれに似たブロックを探そうとします.その探索範囲は,元のブロックの近傍,あるいは,(
use_previous=1
の場合)前回の関数呼び出しで計算された速度分 (velx(x0,y0),vely(x0,y0)) だけ移動したブロックの近傍です.
ピクセルのブロック毎にオプティカルフローを計算します.したがって,速度場のサイズは元の画像よりも小さくなります.この関数は,
prev
の各ブロックに対して,
curr
からそれに似たブロックを探そうとします.その探索範囲は,元のブロックの近傍,あるいは,(
use_previous=1
の場合)前回の関数呼び出しで計算された速度分 (velx(x0,y0),vely(x0,y0)) だけ移動したブロックの近傍です.
CalcOpticalFlowHS¶
- void cvCalcOpticalFlowHS(const CvArr* prev, const CvArr* curr, int usePrevious, CvArr* velx, CvArr* vely, double lambda, CvTermCriteria criteria)¶
2つの画像に対するオプティカルフローを求めます.
パラメタ: - prev – 1番目の画像.8ビット,シングルチャンネル.
- curr – 2番目の画像.8ビット,シングルチャンネル.
- usePrevious – 前回のフレームの速度場を,今回の計算の初期値として利用します.
- velx – オプティカルフローの水平成分.入力画像と同じサイズ,32ビット,浮動小数点型,シングルチャンネル.
- vely – オプティカルフローの垂直成分.入力画像と同じサイズ,32ビット,浮動小数点型,シングルチャンネル.
- lambda – ラグランジュ乗数.
- criteria – 速度計算の停止基準.
この関数は,Horn-Schunck のアルゴリズム Horn81 を用いて,1番目の画像の各ピクセルに対するフローを計算します.
CalcOpticalFlowLK¶
- void cvCalcOpticalFlowLK(const CvArr* prev, const CvArr* curr, CvSize winSize, CvArr* velx, CvArr* vely)¶
2つの画像に対するオプティカルフローを求めます.
パラメタ: - prev – 1番目の画像.8ビット,シングルチャンネル.
- curr – 2番目の画像.8ビット,シングルチャンネル.
- winSize – ピクセルをグループ化するための平均化窓のサイズ.
- velx – オプティカルフローの水平成分.入力画像と同じサイズ,32ビット,浮動小数点型,シングルチャンネル.
- vely – オプティカルフローの垂直成分.入力画像と同じサイズ,32ビット,浮動小数点型,シングルチャンネル.
この関数は,Lucas-Kanade のアルゴリズム Lucas81 を用いて,1番目の画像の各ピクセルに対するフローを計算します.
CalcOpticalFlowPyrLK¶
- void cvCalcOpticalFlowPyrLK(const CvArr* prev, const CvArr* curr, CvArr* prevPyr, CvArr* currPyr, const CvPoint2D32f* prevFeatures, CvPoint2D32f* currFeatures, int count, CvSize winSize, int level, char* status, float* track_error, CvTermCriteria criteria, int flags)¶
Lucas-Kanade法を画像ピラミッドを利用して反復実行することにより,疎な特徴集合に対するオプティカルフローを求めます.
パラメタ: - prev – 時間 t における1番目のフレーム.
- curr – 時間 t + dt における2番目のフレーム.
- prevPyr – 1番目のフレームに対する画像ピラミッドのバッファ.このポインタが NULL ではない場合,バッファは,レベル 1 から level までの画像ピラミッドを格納するのに十分なサイズでなければいけません.合計 (image_width+8)*image_height/3 バイトが十分なサイズといえます.
- curr_pyr – prevPyr と同様.こちらは2番目のフレームに対して利用されます.
- prevFeatures – フローを検出するのに必要な(特徴)点の配列.
- currFeatures – 2次元座標点の配列.入力特徴の2番目のフレームにおける新しい位置が求められ,ここに格納されます.
- count – 特徴点の個数.
- winSize – 画像ピラミッドの各レベルにおける探索窓のサイズ.
- level – 画像ピラミッドの最大レベル数.これが 0 ならば,画像ピラミッドは利用されません(1レベル). 1 ならば,2レベルまでの画像ピラミッドが利用されます.以降同様.
- status – 配列.特徴点のフローが検出できた場合は,それに対応する要素が 1 にセットされ,そうでない場合は 0 にセットされます.
- track_error – オプション.移動前の特徴点の周辺領域と,移動後の特徴点の周辺領域との差を含む配列. NULL でも構いません.
- criteria – 各レベルの画像ピラミッドの各特徴点に対するフローを求める反復計算の停止基準.
- flags –
雑多なフラグ:
- CV_LKFLOWPyr_A_READY 1番目のフレームに対する画像ピラミッドが事前(この関数の呼び出し前)に計算されています.
- CV_LKFLOWPyr_B_READY 2番目のフレームに対する画像ピラミッドが事前(この関数の呼び出し前)に計算されています.
- CV_LKFLOW_INITIAL_GUESSES currFeatures には,事前(この関数の呼び出し前)に特徴点の初期座標が計算され格納されています.
この関数は,Lucas-Kanade法を利用したオプティカルフロー計算を,画像ピラミッドを利用して数回反復するバージョンの実装です Bouguet00 .以前のビデオフレームの特徴点座標が与えられると,現在のフレームでの座標が計算されます.また,この関数は,サブピクセル精度で座標を検出します.
パラメータ prevPyr と currPyr は,どちらも以下の規則に従います:画像ポインタが0の場合,この関数は内部にバッファを確保後,画像ピラミッドを計算します.そして,処理が終わるとそのバッファは解放されます.画像ポインタが0ではない場合,画像ピラミッドを計算し,指定のバッファにそれを格納します.ただし,フラグ CV_LKFLOWPyr_A[B]_READY が指定されている場合を除きます.また,これらの画像は,ガウシアンピラミッドのデータが入るのに十分な大きさが必要です.関数呼び出し後,両方の画像ピラミッドが計算され,次の関数呼び出しに備えて対応画像の準備完了フラグがセットされます(つまり,通常は,一番最初の関数呼び出し以外は, CV_LKFLOWPyr_A_READY が指定されています).
CamShift¶
- int cvCamShift(const CvArr* prob_image, CvRect window, CvTermCriteria criteria, CvConnectedComp* comp, CvBox2D* box=NULL)¶
物体の中心,サイズ,姿勢を求めます.
パラメタ: - prob_image – 物体のヒストグラムのバックプロジェクション( CalcBackProject を参照).
- window – 探索窓の初期状態.
- criteria – 探索の停止基準.
- comp – 結果として得られる構造体.最終的に収束した探索窓の座標(フィールド comp->rect ),および窓内の全ピクセル値の合計(フィールド comp->area )を含みます.
- box – 物体の概説矩形. NULL でなければ,これが物体のサイズと姿勢を表します
この関数は,CAMSHIFT 物体追跡アルゴリズム Bradski98 の実装です.まず, MeanShift を用いて物体中心を求め,次に,物体のサイズと姿勢を計算します.この関数は, MeanShift 内における反復数を返します.
cv.hpp で宣言されている CamShiftTracker クラスは,この関数を利用したカラー物体追跡器の実装です.
CvConDensation¶
ConDenstation の状態構造体.
typedef struct CvConDensation
{
int MP; // 観測ベクトルの次元数
int DP; // 状態ベクトルの次元数
float* DynamMatr; // 線形動力学モデル
float* State; // 状態ベクトル
int SamplesNum; // サンプル数
float** flSamples; // サンプルベクトルの配列
float** flNewSamples; // サンプルベクトルのテンポラリ配列
float* flConfidence; // 各サンプルの確からしさ
float* flCumulative; // 確からしさの累積値
float* Temp; // テンポラリベクトル
float* RandomSample; // サンプル集合を更新するためのランダムベクトル
CvRandState* RandS; // ランダムベクトルを生成するための構造体の配列
} CvConDensation;
構造体 CvConDensation は,CONditional DENSity propagATION 追跡器の状態を保存します.なお,このアルゴリズムに関する情報は, http://www.dai.ed.ac.uk/CVonline/LOCAL_COPIES/ISARD1/condensation.html で知ることができます.
CreateConDensation¶
- CvConDensation* cvCreateConDensation(int dynam_params, int measure_params, int sample_count)¶
ConDensationフィルタ構造体の領域を確保します.
パラメタ: - dynam_params – 状態ベクトルの次元数.
- dynam_params – 状態ベクトルの次元数.
- sample_count – サンプル数.
この関数は,構造体 CvConDensation を作成し,その構造体へのポインタを返します.
ConDensInitSampleSet¶
- void cvConDensInitSampleSet(CvConDensation* condens, CvMat* lower_bound, CvMat* upper_bound)¶
ConDensation アルゴリズムのためのサンプル集合を初期化します.
パラメタ: - condens – 初期化される構造体へのポインタ.
- lower_bound – 各次元における下限を表すベクトル.
- upper_bound – 各次元における上限を表すベクトル.
この関数は,構造体 condens 内のサンプル配列を,指定範囲内の値で埋めます.
CvKalman¶
- CvKalman¶
カルマンフィルタの状態構造体.
typedef struct CvKalman
{
int MP; /* 観測ベクトルの次元数 */
int DP; /* 状態ベクトルの次元数 */
int CP; /* 制御ベクトルの次元数 */
/* 後方互換性のためのフィールド */
#if 1
float* PosterState; /* =state_pre->data.fl */
float* PriorState; /* =state_post->data.fl */
float* DynamMatr; /* =transition_matrix->data.fl */
float* MeasurementMatr; /* =measurement_matrix->data.fl */
float* MNCovariance; /* =measurement_noise_cov->data.fl */
float* PNCovariance; /* =process_noise_cov->data.fl */
float* KalmGainMatr; /* =gain->data.fl */
float* PriorErrorCovariance;/* =error_cov_pre->data.fl */
float* PosterErrorCovariance;/* =error_cov_post->data.fl */
float* Temp1; /* temp1->data.fl */
float* Temp2; /* temp2->data.fl */
#endif
CvMat* state_pre; /* 状態の推定値 (x'(k)):
x(k)=A*x(k-1)+B*u(k) */
CvMat* state_post; /* 更新された状態の推定値 (x(k)):
x(k)=x'(k)+K(k)*(z(k)-H*x'(k)) */
CvMat* transition_matrix; /* システムの時間遷移に関する線形モデル (A) */
CvMat* control_matrix; /* 制御行列 (B)
(制御していない場合は,これは利用されません) */
CvMat* measurement_matrix; /* 観測行列 (H) */
CvMat* process_noise_cov; /* プロセスノイズ(時間遷移に関するノイズ)の共分散行列 (Q) */
CvMat* measurement_noise_cov; /* 観測ノイズの共分散行列 (R) */
CvMat* error_cov_pre; /* 今の時刻の誤差行列 (P'(k)):
P'(k)=A*P(k-1)*At + Q*/
CvMat* gain; /* 最適カルマンゲイン (K(k)):
K(k)=P'(k)*Ht*inv(H*P'(k)*Ht+R)*/
CvMat* error_cov_post; /* 更新された誤差の共分散行列 (P(k)):
P(k)=(I-K(k)*H)*P'(k) */
CvMat* temp1; /* テンポラリ行列 */
CvMat* temp2;
CvMat* temp3;
CvMat* temp4;
CvMat* temp5;
}
CvKalman;
構造体 CvKalman は,カルマンフィルタの状態を記憶しておくために利用されます.これは,関数 CreateKalman によって作成,関数 KalmanPredict と KalmanCorrect によって更新され ,関数 ReleaseKalman によって解放され ます.通常,この構造体は標準カルマンフィルタで利用されます(以下の表記法と式は,優れたカルマンフィルタのチュートリアルである Welch95 から引用しました)
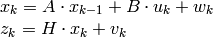
ここで,
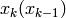 : 時刻
: 時刻
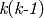 におけるシステムの状態,
におけるシステムの状態,
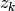 : 時刻
: 時刻
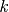 における観測値,
における観測値,
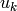 : 時刻
: 時刻
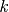 における制御入力,を表します.
における制御入力,を表します.
また,
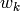 と
と
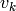 はそれぞれ,正規分布に従うプロセスノイズ,および観測ノイズです:
はそれぞれ,正規分布に従うプロセスノイズ,および観測ノイズです:
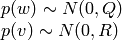
つまり,
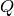 プロセスノイズの共分散行列,定数あるいは変数,
プロセスノイズの共分散行列,定数あるいは変数,
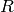 観測ノイズの共分散行列,定数あるいは変数
観測ノイズの共分散行列,定数あるいは変数
標準カルマンフィルタの場合,全ての行列:A, B, H, Q, R は, CreateKalman によって構造体 CvKalman が確保された後で1度だけ初期化されます.しかし,拡張カルマンフィルタの式を現在のシステム状態周辺において線形化することで,拡張カルマンフィルタをシミュレートするために,同じ構造体と同じ関数が利用されることがあります.この場合,A, B, H (おそらく,Q と R も)毎ステップ更新されます.
CreateKalman¶
- CvKalman* cvCreateKalman(int dynam_params, int measure_params, int control_params=0)¶
カルマンフィルタの構造の領域を確保します.
パラメタ: - dynam_params – 状態ベクトルの次元数.
- measure_params – 観測ベクトルの次元数.
- control_params – 制御ベクトルの次元数.
この関数は,構造体 CvKalman と,そのメンバであるすべての行列の領域を確保し,何らかの方法で初期化します.
KalmanCorrect¶
- const CvMat* cvKalmanCorrect(CvKalman* kalman, const CvMat* measurement)¶
モデルの状態を更新します.
パラメタ: - kalman – 更新されるカルマンフィルタ構造体へのポインタ.
- measurement – 観測ベクトルを含む CvMat.
この関数は,モデル状態に対する観測ベクトルが与えられると,それに基づき確率モデル状態を更新します:
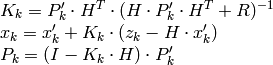
ここで
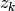 |
与えられた観測 ( mesurement パラメータ) |
|---|---|
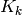 |
カルマン「ゲイン」行列 |
です. この関数は,更新された状態を kalman->state_post に格納し,そのポインタを返します.
Example. Using Kalman filter to track a rotating point
#include "cv.h"
#include "highgui.h"
#include <math.h>
int main(int argc, char** argv)
{
/* 行列データ A */
const float A[] = { 1, 1, 0, 1 };
IplImage* img = cvCreateImage( cvSize(500,500), 8, 3 );
CvKalman* kalman = cvCreateKalman( 2, 1, 0 );
/* 状態 (phi, delta_phi) - 角度,角度の変化量 */
CvMat* state = cvCreateMat( 2, 1, CV_32FC1 );
CvMat* process_noise = cvCreateMat( 2, 1, CV_32FC1 );
/* phi (角度) だけが観測される */
CvMat* measurement = cvCreateMat( 1, 1, CV_32FC1 );
CvRandState rng;
int code = -1;
cvRandInit( &rng, 0, 1, -1, CV_RAND_UNI );
cvZero( measurement );
cvNamedWindow( "Kalman", 1 );
for(;;)
{
cvRandSetRange( &rng, 0, 0.1, 0 );
rng.disttype = CV_RAND_NORMAL;
cvRand( &rng, state );
memcpy( kalman->transition_matrix->data.fl, A, sizeof(A));
cvSetIdentity( kalman->measurement_matrix, cvRealScalar(1) );
cvSetIdentity( kalman->process_noise_cov, cvRealScalar(1e-5) );
cvSetIdentity( kalman->measurement_noise_cov, cvRealScalar(1e-1) );
cvSetIdentity( kalman->error_cov_post, cvRealScalar(1));
/* 初期状態をランダムに選択 */
cvRand( &rng, kalman->state_post );
rng.disttype = CV_RAND_NORMAL;
for(;;)
{
#define calc_point(angle) \
cvPoint( cvRound(img->width/2 + img->width/3*cos(angle)), \
cvRound(img->height/2 - img->width/3*sin(angle)))
float state_angle = state->data.fl[0];
CvPoint state_pt = calc_point(state_angle);
/* 点の位置を推定 */
const CvMat* prediction = cvKalmanPredict( kalman, 0 );
float predict_angle = prediction->data.fl[0];
CvPoint predict_pt = calc_point(predict_angle);
float measurement_angle;
CvPoint measurement_pt;
cvRandSetRange( &rng,
0,
sqrt(kalman->measurement_noise_cov->data.fl[0]),
0 );
cvRand( &rng, measurement );
/* 観測値を生成 */
cvMatMulAdd( kalman->measurement_matrix, state, measurement, measurement );
measurement_angle = measurement->data.fl[0];
measurement_pt = calc_point(measurement_angle);
/* 点をプロット */
#define draw_cross( center, color, d ) \
cvLine( img, cvPoint( center.x - d, center.y - d ), \
cvPoint( center.x + d, center.y + d ), \
color, 1, 0 ); \
cvLine( img, cvPoint( center.x + d, center.y - d ), \
cvPoint( center.x - d, center.y + d ), \
color, 1, 0 )
cvZero( img );
draw_cross( state_pt, CV_RGB(255,255,255), 3 );
draw_cross( measurement_pt, CV_RGB(255,0,0), 3 );
draw_cross( predict_pt, CV_RGB(0,255,0), 3 );
cvLine( img, state_pt, predict_pt, CV_RGB(255,255,0), 3, 0 );
/* カルマンフィルタの状態を更新 */
cvKalmanCorrect( kalman, measurement );
cvRandSetRange( &rng,
0,
sqrt(kalman->process_noise_cov->data.fl[0]),
0 );
cvRand( &rng, process_noise );
cvMatMulAdd( kalman->transition_matrix,
state,
process_noise,
state );
cvShowImage( "Kalman", img );
code = cvWaitKey( 100 );
if( code > 0 ) /* キーを押すと現在のシミュレーションを終了 */
break;
}
if( code == 27 ) /* ESC キーでプログラム終了 */
break;
}
return 0;
}
KalmanPredict¶
- const CvMat* cvKalmanPredict(CvKalman* kalman, const CvMat* control=NULL)¶
次のモデル状態を推定します.
パラメタ: - kalman – カルマンフィルタの状態.
- control – 制御ベクトル
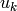 , 制御入力が存在しない場合( control_params =0 )のみ NULL.
, 制御入力が存在しない場合( control_params =0 )のみ NULL.
この関数は,現在の状態から次の確率モデル状態を推定し, kalman->state_pre に格納します:
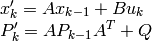
ここで
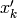 |
状態の推定値 kalman->state_pre , |
|---|---|
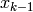 |
前回の更新された状態の推定値 kalman->state_post (最初は何らかの方法で初期化される,デフォルトではゼロベクトル), |
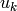 |
制御入力 ( control パラメータ), |
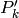 |
今の時刻の誤差の共分散行列 kalman->error_cov_pre |
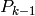 |
前回の更新された誤差の共分散行列 kalman->error_cov_post (最初は何らかの方法で初期化される,デフォルトでは単位行列), |
この関数は,状態の推定値を返します.
KalmanUpdateByMeasurement¶
KalmanCorrect と同義
KalmanUpdateByTime¶
KalmanPredict と同義
MeanShift¶
- int cvMeanShift(const CvArr* prob_image, CvRect window, CvTermCriteria criteria, CvConnectedComp* comp)¶
バックプロジェクション上の物体中心を求めます.
パラメタ: - prob_image – 物体のヒストグラムのバックプロジェクション( CalcBackProject を参照してください).
- window – 探索窓の初期状態.
- criteria – 探索の停止基準.
- comp – 結果として得られる構造体.最終的に収束した探索窓の座標(フィールド comp->rect ),および窓内の全ピクセル値の合計(フィールド comp->area )を含みます.
この関数は,物体のバック工プロジェクションと探索窓の初期位置が与えられると,その物体の中心を求めるための反復計算を行います.反復計算は,探索窓中心の移動量が与えられた閾値より小さくなるか,あるいは関数の反復数が最大値に達するまで続けられます.また,この関数は,その反復数を返します.
ReleaseConDensation¶
- void cvReleaseConDensation(CvConDensation** condens)¶
ConDensationフィルタ構造体を解放します.
パラメタ: - condens – 解放される構造体へのダブルポインタ.
この関数は,構造体 condens と,この構造体のために確保されたメモリすべてを解放します.
SegmentMotion¶
- CvSeq* cvSegmentMotion(const CvArr* mhi, CvArr* seg_mask, CvMemStorage* storage, double timestamp, double seg_thresh)¶
モーション全体を個別のモーションに分解します.
パラメタ: - mhi – モーション履歴画像.
- seg_mask – 検出されたマスクが保存される画像.シングルチャンネル,32ビット,浮動小数点型.
- storage – モーション連結成分のシーケンスが保存されるメモリストレージ.
- timestamp – ミリ秒単位,あるいは別の単位で表される現在時間.
- seg_thresh – 分割の閾値.モーション履歴の間隔と同じか,それよりも大きい値の方が良いでしょう.
この関数は,すべてのモーション成分を検出し,それぞれ個別の値を用いて seg_mask にマークします.これは,各モーション成分毎に,構造体 CvConnectedComp のシーケンスを返します.その後,特定の成分を抽出するマスク Cmp を利用し, CalcGlobalOrientation によって全てのモーション成分のモーション方向が計算されます.
SnakeImage¶
- void cvSnakeImage(const IplImage* image, CvPoint* points, int length, float* alpha, float* beta, float* gamma, int coeff_usage, CvSize win, CvTermCriteria criteria, int calc_gradient=1)¶
そのエネルギーが最小となるように輪郭位置を変更します.
パラメタ: - image – 入力画像,あるいは外部エネルギー場.
- points – 輪郭点 (snake).
- length – 輪郭中の点数.
- alpha – 連続エネルギーの重み.1つの浮動小数点数,あるいは長さ length の浮動小数点型の配列.後者の場合,1つの要素が1つの輪郭点に対応します.
- beta – 曲率エネルギーの重み. alpha と同様.
- gamma – 画像エネルギーの重み. alpha と同様.
- coeff_usage –
前述の3つのパラメータの使用法:
- CV_VALUE の場合, alpha, beta, gamma の各パラメータは,全ての輪郭点で利用される1つの値へのポインタです.
- CV_ARRAY の場合, alpha, beta, gamma の各パラメータは,全ての輪郭点に対しての個別の係数を要素にもつ配列へのポインタです.全ての配列サイズは,輪郭サイズと同じでなければいけません.
- win – 最小値探索に用いられる各輪郭点の近傍領域サイズ. win.width および win.height は奇数でなければいけません.
- criteria – 停止基準.
- calc_gradient – 勾配フラグ.0以外の場合,この関数は,各画像ピクセルに対する勾配の強さを計算し,それをエネルギー場として扱います.そうでない場合,入力画像はそのまま扱われます.
この関数は,内部エネルギーと外部エネルギーの総和が最小になるように輪郭点を更新します.内部エネルギーは,輪郭形状に依存します(滑らかな輪郭ほど,内部エネルギーが小さくなります).また,外部エネルギーはエネルギー場に依存し,画像勾配を用いる場合は,画像エッジのようにエネルギーが極小値をとる場所において最小になります.
パラメータ criteria.epsilon は,1回の計算で最低何個の輪郭点が移動すれば反復計算が継続されるか,を規定します.
ある試行において,移動する輪郭点の個数が criteria.epsilon よりも少ないか,あるいは,関数の反復計算回数が criteria.max_iter に達した場合,この関数は終了します.
UpdateMotionHistory¶
- void cvUpdateMotionHistory(const CvArr* silhouette, CvArr* mhi, double timestamp, double duration)¶
動作を表すシルエット画像を用いて,モーション履歴画像を更新します.
パラメタ: - silhouette – モーションが発生した場所が 0 以外のピクセル値をもつシルエットマスク.
- mhi – この関数によって更新される,モーション履歴画像(シングルチャンネル,32ビット浮動小数点型).
- timestamp – ミリ秒単位,あるいは別の単位で表される現在時間.
- duration – timestamp と同じ単位で表される,モーションの最大持続時間.
この関数は,モーション履歴画像を以下のように更新します:
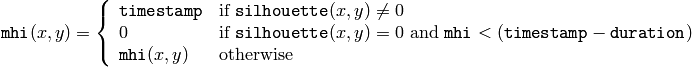
つまり,モーションが発生した場所のMHI(モーション履歴画像)ピクセルには,現在のタイムスタンプがセットされ,モーションが発生からある程度以上時間が経ったピクセルの値はクリアされます.
ヘルプとフィードバック
お探しの情報が見つかりませんか?- ユーザグループ/メーリングリスト (英語)で質問してみてください.
- このドキュメントに誤りなどを見つけたらbug report まで報告してください.また,日本語訳に関する誤りや指摘はOpenCV.jpまでお願いします.
