クラスタリング

cv::kmeans

Comments from the Wiki

double kmeans(const Mat& samples, int clusterCount, Mat& labels, TermCriteria termcrit, int attempts, int flags, Mat* centers)

クラスタ中心を求め，入力サンプルを各クラスタにグループ分けします．

パラメタ:

• samples – 入力サンプルの浮動小数点型行列．1行が1つのサンプルを表します
• clusterCount – サンプル集合を分割するクラスタ数
• labels – 整数型の入出力配列．各要素が属するクラスタのインデックスを格納します
• termcrit – 反復数の最大値 および/または 精度（連続する試行間でクラスタ中心が移動する距離）を指定します
• attempts – このアルゴリズムが，異なる初期ラベルを与えられて実行される回数．このアルゴリズムは，最もコンパクトな分割を行うラベル（最後のパラメータを参照してください）を返します
• flags –

  以下の値をとることができます：

  • KMEANS_RANDOM_CENTERS 各試行で，ランダムな初期中心が選択されます
  • KMEANS_PP_CENTERS Arthur および Vassilvitskiiによる kmeans++ の中心初期化手法が利用されます
  • KMEANS_USE_INITIAL_LABELS 最初の試行で（だけ）は，ランダムに生成されるラベルの代わりに，ユーザが与えたラベルを初期推定値として利用します．2回目以降の試行では，ランダムまたは半ランダム（手法を指定するために KMEANS_*_CENTERS フラグの1つを利用します）に選択された中心が用いられます
• centers – クラスタ中心の出力行列．1つの行が1つのクラスタ中心を表します

関数 kmeans は， clusterCount 個のクラスタの中心を求め，入力サンプルを各クラスタに分類する k-means アルゴリズムの実装です．出力として， samples 行列の 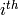行目のサンプルが属するクラスタの（0基準の）インデックスが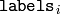， に格納されます．

この関数は，次のように計算されるコンパクト尺度を返します．

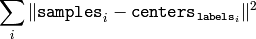
全試行の終了後，最もよい（小さい）値が選択され，それに対応するラベルとコンパクト尺度が戻り値として返されます．

また，基本的に次のようにして，ユーザはこの関数の基本機能だけを利用することができます．まず，試行回数を1にセットし，フラグ（ flags = KMEANS_USE_INITIAL_LABELS ）をセットして，独自アルゴリズムによりラベルを毎回初期化します そして，最良の（最もコンパクトな）クラスタリングを選択します．

cv::partition

Comments from the Wiki

template<typename _Tp, class _EqPredicate> int()

partition(const vector<_Tp>& vec, vector<int>& labels, _EqPredicate predicate=_EqPredicate())

要素の集合を同値クラス（同値類）に分割します．

パラメタ:

• vec – ベクトルで表現された要素の集合
• labels – 出力されるラベルのベクトル． vec と同じ要素数．各ラベル labels[i] は， vec[i] が属する0基準のクラスタインデックスです
• predicate – 同値述語（つまり，2つの引数をとり真偽値を返す関数へのポインタ，あるいは， bool operator()(const _Tp& a, const _Tp& b) メソッドを持つクラスのインスタンスへのポインタ）．この述語は，要素が確実に同じクラスならば真値を返し，同じクラスの可能性がある（同じクラスではない可能性がある）場合は偽値を返します

汎用関数 partition は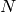， 個の要素の集合を1つまたは複数の同値類に分割する 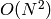のアルゴリズムの実装です．これについては http://en.wikipedia.org/wiki/Disjoint-set_data_structure で説明されています．また，この関数は，同値類の個数を返します．