基本構造体¶
DataType¶
OpenCV のその他のプリミティブなデータ型に対する “traits” クラステンプレート.
template<typename _Tp> class DataType
{
// value_type は常に _Tp と等しくなります.
typedef _Tp value_type;
// _Tp の処理で利用される中間型です.
// uchar, signed char, unsigned char, signed short, int に対しては int ,
// float に対しては float , double に対しては double , ...
typedef <...> work_type;
// マルチチャンネルデータの場合,これは各チャンネルのデータ型になります.
typedef <...> channel_type;
enum
{
// CV_8U ... CV_64F
depth = DataDepth<channel_type>::value,
// 1 ...
channels = <...>,
// '1u', '4i', '3f', '2d' など.
fmt=<...>,
// CV_8UC3, CV_32FC2 ...
type = CV_MAKETYPE(depth, channels)
};
};
クラステンプレート DataType は,OpenCV の基本的なデータ型や以下の定義に従うその他の型,に対する説明的なクラスです. OpenCV の基本的なデータ型は, unsigned char, bool, unsigned char, signed char, unsigned short, signed short, int, float, double の 1 つ,あるいは, 1 つの型の値のタプルで,その場合タプル内の値はすべて同じ型になります. OpenCV の CvMat の表記法 CV _ 8U ... CV _ 32FC3, CV _ 64FC2 に慣れているならば, 基本的な型は CV_<bit-depth>{U|S|F}C<number_of_channels> の形式で一意な識別子を与えることができるもの,としても定義できます. Vec は,この基本的なデータ型の 1 つのインスタンスを格納できる OpenCV の汎用的な構造です. また, std::vector , Mat , Mat_ , SparseMat , SparseMat_ や, Vec() のインスタンスを格納できるその他のコンテナは,このような型の複数のインスタンスを格納できます.
DataType クラスは基本的に,対象となるクラスにフィールドやメソッドを追加せずに(C/C++ の基本的なデータ型に何かを追加するのは実際に不可能です),このような基本的なデータ型の説明を提供するために利用されます.このテクニックは,C++ では traits クラスとして知られています.使われるのは DataType 自身ではなく,以下のように特殊化したものです:
template<> class DataType<uchar>
{
typedef uchar value_type;
typedef int work_type;
typedef uchar channel_type;
enum { channel_type = CV_8U, channels = 1, fmt='u', type = CV_8U };
};
...
template<typename _Tp> DataType<std::complex<_Tp> >
{
typedef std::complex<_Tp> value_type;
typedef std::complex<_Tp> work_type;
typedef _Tp channel_type;
// DataDepth は別の traits クラス
enum { depth = DataDepth<_Tp>::value, channels=2,
fmt=(channels-1)*256+DataDepth<_Tp>::fmt,
type=CV_MAKETYPE(depth, channels) };
};
...
このクラスの主な目的は,コンパイル時の型情報を OpenCV と互換性のあるデータ型識別子に変換することです.例えば:
// 30x40 の浮動小数点型行列を確保します.
Mat A(30, 40, DataType<float>::type);
Mat B = Mat_<std::complex<double> >(3, 3);
// 以下の文は, 6, 2 を表示します /* つまり, depth == CV_64F, channels == 2 */
cout << B.depth() << ", " << B.channels() << endl;
つまり,この traits クラスは,ユーザがどんなデータ型を使用しているかを,たとえそのデータ型が OpenCV の組み込み型ではないとしても,OpenCV に教えるために利用されます (OpenCV は適切に特殊化されたクラステンプレート DataType<complex<_Tp> > を定義するので,上述の行列 B の初期化はコンパイルされます)また,この機構は generic algorithm の実装に役立ちます(OpenCV内でもそのように使われています).
Point_¶
2 次元座標上の点のためのクラステンプレート.
template<typename _Tp> class Point_
{
public:
typedef _Tp value_type;
Point_();
Point_(_Tp _x, _Tp _y);
Point_(const Point_& pt);
Point_(const CvPoint& pt);
Point_(const CvPoint2D32f& pt);
Point_(const Size_<_Tp>& sz);
Point_(const Vec<_Tp, 2>& v);
Point_& operator = (const Point_& pt);
template<typename _Tp2> operator Point_<_Tp2>() const;
operator CvPoint() const;
operator CvPoint2D32f() const;
operator Vec<_Tp, 2>() const;
// 内積を計算します. (this->x*pt.x + this->y*pt.y)
_Tp dot(const Point_& pt) const;
// 倍精度の演算を用いて内積を計算します.
double ddot(const Point_& pt) const;
// この点が矩形 "r" 内に入っていれば真値を返します.
bool inside(const Rect_<_Tp>& r) const;
_Tp x, y;
};
このクラスは,その座標値
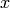 と
と
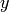 によって指定される 2 次元の点を表現します.
このクラスのインスタンスは, C の構造体である
CvPoint
や
CvPoint2D32f
と交換可能です.また,点の座標を指定の型に変換するためのキャスト演算子も存在します.浮動小数点型座標から整数座標への変換は,丸めることで行われます.通常は,それぞれの座標に対して
saturate_cast
演算を行います.上述の宣言にあるクラスメンバに加えて,座標点に対する以下の処理が実装されています:
によって指定される 2 次元の点を表現します.
このクラスのインスタンスは, C の構造体である
CvPoint
や
CvPoint2D32f
と交換可能です.また,点の座標を指定の型に変換するためのキャスト演算子も存在します.浮動小数点型座標から整数座標への変換は,丸めることで行われます.通常は,それぞれの座標に対して
saturate_cast
演算を行います.上述の宣言にあるクラスメンバに加えて,座標点に対する以下の処理が実装されています:
pt1 = pt2 + pt3;
pt1 = pt2 - pt3;
pt1 = pt2 * a;
pt1 = a * pt2;
pt1 += pt2;
pt1 -= pt2;
pt1 *= a;
double value = norm(pt); // L2 ノルム
pt1 == pt2;
pt1 != pt2;
利便性のために,以下のように型の別名が定義されています:
typedef Point_<int> Point2i;
typedef Point2i Point;
typedef Point_<float> Point2f;
typedef Point_<double> Point2d;
ここでは,短い例を示します:
Point2f a(0.3f, 0.f), b(0.f, 0.4f);
Point pt = (a + b)*10.f;
cout << pt.x << ", " << pt.y << endl;
Point3_¶
3 次元座標上の点のためのクラステンプレート.
template<typename _Tp> class Point3_
{
public:
typedef _Tp value_type;
Point3_();
Point3_(_Tp _x, _Tp _y, _Tp _z);
Point3_(const Point3_& pt);
explicit Point3_(const Point_<_Tp>& pt);
Point3_(const CvPoint3D32f& pt);
Point3_(const Vec<_Tp, 3>& v);
Point3_& operator = (const Point3_& pt);
template<typename _Tp2> operator Point3_<_Tp2>() const;
operator CvPoint3D32f() const;
operator Vec<_Tp, 3>() const;
_Tp dot(const Point3_& pt) const;
double ddot(const Point3_& pt) const;
_Tp x, y, z;
};
このクラスは,その座標値
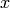 ,
,
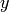 ,
,
 によって指定される 3 次元の点を表現します.
このクラスのインスタンスは, C の構造体
CvPoint2D32f
と交換可能です.
Point_
の場合と同様に,3 次元点の座標を別の型に変換する事が可能で,さらにベクトル計算や比較演算もサポートされています.
によって指定される 3 次元の点を表現します.
このクラスのインスタンスは, C の構造体
CvPoint2D32f
と交換可能です.
Point_
の場合と同様に,3 次元点の座標を別の型に変換する事が可能で,さらにベクトル計算や比較演算もサポートされています.
以下のような型の別名が利用可能です:
typedef Point3_<int> Point3i;
typedef Point3_<float> Point3f;
typedef Point3_<double> Point3d;
Size_¶
画像や矩形のサイズを表現するためのクラステンプレート.
template<typename _Tp> class Size_
{
public:
typedef _Tp value_type;
Size_();
Size_(_Tp _width, _Tp _height);
Size_(const Size_& sz);
Size_(const CvSize& sz);
Size_(const CvSize2D32f& sz);
Size_(const Point_<_Tp>& pt);
Size_& operator = (const Size_& sz);
_Tp area() const;
operator Size_<int>() const;
operator Size_<float>() const;
operator Size_<double>() const;
operator CvSize() const;
operator CvSize2D32f() const;
_Tp width, height;
};
Size_ クラスは, 2 つのメンバが x と y ではなく width と height という名前になっていることを除けば, Point_ と同じです.この構造は,古い OpenCV の構造体 CvSize や CvSize2D32f に対して相互に変換可能です.また,このクラスでも Point_ に対する計算や比較演算と同様のものが利用できます.
OpenCVでは,型の別名を以下の用に定義しています:
typedef Size_<int> Size2i;
typedef Size2i Size;
typedef Size_<float> Size2f;
Rect_¶
2 次元の矩形を表現するためのクラステンプレート.
template<typename _Tp> class Rect_
{
public:
typedef _Tp value_type;
Rect_();
Rect_(_Tp _x, _Tp _y, _Tp _width, _Tp _height);
Rect_(const Rect_& r);
Rect_(const CvRect& r);
// (x, y) <- org, (width, height) <- sz
Rect_(const Point_<_Tp>& org, const Size_<_Tp>& sz);
// (x, y) <- min(pt1, pt2), (width, height) <- max(pt1, pt2) - (x, y)
Rect_(const Point_<_Tp>& pt1, const Point_<_Tp>& pt2);
Rect_& operator = ( const Rect_& r );
// Point_<_Tp>(x, y) を返します
Point_<_Tp> tl() const;
// Point_<_Tp>(x+width, y+height) を返します
Point_<_Tp> br() const;
// Size_<_Tp>(width, height) を返します
Size_<_Tp> size() const;
// width*height を返します
_Tp area() const;
operator Rect_<int>() const;
operator Rect_<float>() const;
operator Rect_<double>() const;
operator CvRect() const;
// x <= pt.x && pt.x < x + width &&
// y <= pt.y && pt.y < y + height ? true : false
bool contains(const Point_<_Tp>& pt) const;
_Tp x, y, width, height;
};
矩形は,左上コーナの座標(OpenCV ではデフォルトで, Rect_::x と Rect_::y を左上コーナーと解釈しますが,ユーザのアルゴリズムでは x と y を左下のコーナから数える可能性もあります)と,矩形の幅と高さによって表現されます.
OpenCV におけるもう 1 つの前提は,矩形の上側と左側の境界線は矩形に含まれ,右側と下側の境界線は含まれない,ということです.例えば,以下のような場合に, Rect_::contains メソッドは true を返します.
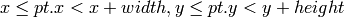
OpenCV では,画像の ROI ( ROIは Rect_<int> によって指定されます)を処理するループは以下のように実装されます:
for(int y = roi.y; y < roi.y + rect.height; y++)
for(int x = roi.x; x < roi.x + rect.width; x++)
{
// ...
}
クラスのメンバに加えて,矩形に対する以下の処理が実装されています:
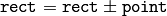 (あるオフセット分だけ矩形を移動する)
(あるオフセット分だけ矩形を移動する)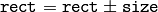 (ある量だけ矩形を縮小あるいは拡大する)
(ある量だけ矩形を縮小あるいは拡大する)- rect += point, rect -= point, rect += size, rect -= size (複合代入)
- rect = rect1 & rect2 (矩形の共通部分)
- rect = rect1 | rect2 ( rect2 と rect3 を含む最小面積の矩形)
- rect &= rect1, rect |= rect1 (上記に相当する複合代入)
- rect == rect1, rect != rect1 (矩形同士の比較)
[例] ここでは,矩形同士における半順序化がどのように決定されているのかを示します(rect1
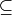 rect2):
rect2):
template<typename _Tp> inline bool
operator <= (const Rect_<_Tp>& r1, const Rect_<_Tp>& r2)
{
return (r1 & r2) == r1;
}
利便性のため,以下のような型の別名が利用可能です:
typedef Rect_<int> Rect;
RotatedRect¶
回転を考慮した矩形.
class RotatedRect
{
public:
// コンストラクタ
RotatedRect();
RotatedRect(const Point2f& _center, const Size2f& _size, float _angle);
RotatedRect(const CvBox2D& box);
// 回転した矩形に対する,最小の(回転していない)外接矩形を返します
Rect boundingRect() const;
// CvBox2D に対する後方互換性
operator CvBox2D() const;
// 矩形の重心
Point2f center;
// サイズ
Size2f size;
// degree で表現される回転角度
float angle;
};
RotatedRect クラスは,古い CvBox2D を置き換え,それと完全な互換性を保ちます.
TermCriteria¶
反復アルゴリズムのための停止基準.
class TermCriteria
{
public:
enum { COUNT=1, MAX_ITER=COUNT, EPS=2 };
// コンストラクタ
TermCriteria();
// type は, MAX_ITER, EPS, MAX_ITER+EPS の内の1つです.
// type = MAX_ITER の場合は,反復回数だけが問題になります.
// type = EPS の場合は,要求精度(イプシロン)だけが問題になります.
// (もっとも,大抵のアルゴリズムでは反復回数に何らかの制限を設けますが)
// type = MAX_ITER + EPS の場合は,反復回数が既定値に達するか,
// あるいは,要求精度が達成された場合にアルゴリズムが停止します.
TermCriteria(int _type, int _maxCount, double _epsilon);
TermCriteria(const CvTermCriteria& criteria);
operator CvTermCriteria() const;
int type;
int maxCount;
double epsilon;
};
TermCriteria は,古い CvTermCriteria を置き換え,それと完全な互換性を保ちます.
Matx¶
小さい行列のためのクラステンプレート.
template<typename T, int m, int n> class Matx
{
public:
typedef T value_type;
enum { depth = DataDepth<T>::value, channels = m*n,
type = CV_MAKETYPE(depth, channels) };
// 様々なメソッド
...
Tp val[m*n];
};
typedef Matx<float, 1, 2> Matx12f;
typedef Matx<double, 1, 2> Matx12d;
...
typedef Matx<float, 1, 6> Matx16f;
typedef Matx<double, 1, 6> Matx16d;
typedef Matx<float, 2, 1> Matx21f;
typedef Matx<double, 2, 1> Matx21d;
...
typedef Matx<float, 6, 1> Matx61f;
typedef Matx<double, 6, 1> Matx61d;
typedef Matx<float, 2, 2> Matx22f;
typedef Matx<double, 2, 2> Matx22d;
...
typedef Matx<float, 6, 6> Matx66f;
typedef Matx<double, 6, 6> Matx66d;
このクラスは,コンパイル時に型とサイズが既知である小さい行列を表します.より柔軟な型が必要な場合は, Mat を利用してください.行列 M の要素には, M(i,j) という表記でアクセス可能です. また,一般的な行列演算の大部分( MatrixExpressions を参照してください)が,利用可能です. Matx に実装されていない操作が必要な場合は,その行列を Mat に変換したり,そこから戻したりすることも簡単に行えます.
Matx33f m(1, 2, 3,
4, 5, 6,
7, 8, 9);
cout << sum(Mat(m*m.t())) << endl;
Vec¶
短い数値ベクトル用のクラステンプレート.
template<typename T, int cn> class Vec : public Matx<T, cn, 1>
{
public:
typedef T value_type;
enum { depth = DataDepth<T>::value, channels = cn,
type = CV_MAKETYPE(depth, channels) };
// 様々なメソッド
};
typedef Vec<uchar, 2> Vec2b;
typedef Vec<uchar, 3> Vec3b;
typedef Vec<uchar, 4> Vec4b;
typedef Vec<short, 2> Vec2s;
typedef Vec<short, 3> Vec3s;
typedef Vec<short, 4> Vec4s;
typedef Vec<int, 2> Vec2i;
typedef Vec<int, 3> Vec3i;
typedef Vec<int, 4> Vec4i;
typedef Vec<float, 2> Vec2f;
typedef Vec<float, 3> Vec3f;
typedef Vec<float, 4> Vec4f;
typedef Vec<float, 6> Vec6f;
typedef Vec<double, 2> Vec2d;
typedef Vec<double, 3> Vec3d;
typedef Vec<double, 4> Vec4d;
typedef Vec<double, 6> Vec6d;
Vec は, Matx の特別な場合です. Vec<T,2> と Point_ は相互に変換可能で, Vec<T,3> と Point3_ も同様です.また, Vec<T,4> は CvScalar や Scalar に変換することができます. Vec の要素にアクセスするには, operator[] を利用します.また,期待されるベクトル演算もすべて実装されています:
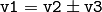 ,
,
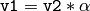 ,
,
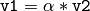 (さらに,それぞれに相当する複合代入演算.これらの操作は,計算結果のベクトル要素に
saturate_cast.3C.3E
を適用することに注意してください)
(さらに,それぞれに相当する複合代入演算.これらの操作は,計算結果のベクトル要素に
saturate_cast.3C.3E
を適用することに注意してください)- v1 == v2, v1 != v2
- norm(v1)
(
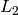 -norm)
-norm)
Vec クラスは,マルチチャンネル配列のピクセルタイプを記述するために利用されています. Mat_ の説明を参照してください.
Scalar_¶
4-要素ベクトル.
template<typename _Tp> class Scalar_ : public Vec<_Tp, 4>
{
public:
Scalar_();
Scalar_(_Tp v0, _Tp v1, _Tp v2=0, _Tp v3=0);
Scalar_(const CvScalar& s);
Scalar_(_Tp v0);
static Scalar_<_Tp> all(_Tp v0);
operator CvScalar() const;
template<typename T2> operator Scalar_<T2>() const;
Scalar_<_Tp> mul(const Scalar_<_Tp>& t, double scale=1 ) const;
template<typename T2> void convertTo(T2* buf, int channels, int unroll_to=0) const;
};
typedef Scalar_<double> Scalar;
クラステンプレート Scalar_ および,その倍精度表現のインスタンス Scalar は, 4 要素のベクトルを表します.これらは Vec<_Tp, 4> から派生しているため,典型的な 4-要素ベクトルとして利用でき,さらに CvScalar と相互に変換可能です. Scalar 型は,OpenCV でピクセル値を処理するために広く利用されており,以前の OpenCV で同様に利用されていた CvScalar を手軽に代替することができます.
Range¶
シーケンス内の,連続した部分シーケンス(別名,スライス)を表します.
class Range
{
public:
Range();
Range(int _start, int _end);
Range(const CvSlice& slice);
int size() const;
bool empty() const;
static Range all();
operator CvSlice() const;
int start, end;
};
このクラスは,行列(
Mat()
)の行または列の区間を指定するため,またその他多くの目的で利用されます.
Range(a,b)
は基本的に, Matlab の
a:b
や Python(numpy) の
a..b
などと等しいものです. Python での表現と同様に,
start
は範囲に含まれる左側の境界,
end
は範囲に含まれない右側の境界です.このような半開区間は,通常
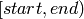 と表記されます.
と表記されます.
スタティックメソッド Range::all() は,丁度 Matlab での ” : ” や Python(numpy) での ” ... ” と同じように「シーケンス全体」あるいは「範囲全体」を意味する特別な変数を返します.
Range を扱う OpenCV のすべてのメソッドおよび関数は,この特別な値 Range::all() をサポートします.しかしもちろん,ユーザ独自の処理では明示的にそれをチェックして対処する必要があります:
void my_function(..., const Range& r, ....)
{
if(r == Range::all()) {
// 全データを処理
}
else {
// [r.start, r.end) を処理
}
}
Ptr¶
参照カウント方式のスマートポインタクラステンプレート.
template<typename _Tp> class Ptr
{
public:
// デフォルトコンストラクタ
Ptr();
// オブジェクトポインタをラップするコンストラクタ
Ptr(_Tp* _obj);
// デストラクタ: release() を呼び出します
~Ptr();
// コピーコンストラクタ. ptr の参照カウントをインクリメントします.
Ptr(const Ptr& ptr);
// 代入演算子.( release() によって)自分の参照カウントをデクリメントし,
// ptr の参照カウンタをインクリメントします.
Ptr& operator = (const Ptr& ptr);
// 参照カウンタをインクリメントします.
void addref();
// 参照カウンタをデクリメントします. 0 になった場合,
// delete_obj() が呼ばれます.
void release();
// ユーザ指定のカスタムオブジェクト削除処理.
// デフォルトでは "delete obj" が呼ばれます.
void delete_obj();
// obj == 0 の場合 true を返します.
bool empty() const;
// オブジェクトのフィールドとメソッドにアクセスする手段を提供します.
_Tp* operator -> ();
const _Tp* operator -> () const;
// 内部のオブジェクトポインタを返します.
// このメソッドのおかげで, _Tp* の代わりに
// Ptr<_Tp> を利用できます.
operator _Tp* ();
operator const _Tp*() const;
protected:
// カプセル化されたオブジェクトポインタ
_Tp* obj;
// 参照カウンタ
int* refcount;
};
Ptr<_Tp> クラスは,対応する型のポインタをラップするクラステンプレートです. これは,Boost ライブラリ( http://www.boost.org/doc/libs/1_40_0/libs/smart_ptr/shared_ptr.htm )や, C++0x 標準にある shared_ptr と同様のものです.
このクラスを利用すると,以下のような事が可能になります:
- C++ のクラスや C の構造体に対するデフォルトコンストラクタ,コピーコンストラクタ,代入演算子が実現できます.ファイルやウィンドウ, mutex , socket などのオブジェクトに対して,コピーコンストラクタや代入演算子を定義するのは難しい事です.一方で,OpenCV の複雑な分類器のようなオブジェクトに対しては,コピーコンストラクタが存在せず,実装するのも簡単ではありません.また,OpenCV やユーザ自身のデータ構造体の中には C で書かれたものもあるでしょう.しかし,コピーコンストラクタやデフォルトコンストラクタは,プログラミングを非常に簡単にします.さらに,(例えば, STL のコンテナなどで)必要になる事も多いでしょう.このような複雑なオブジェクト TObj へのポインタを Ptr<TObj> という風にラッピングする事で,必要とするすべてのコンストラクタや割り当て演算子を自動的に得ることができます.
- 上述の処理はデータサイズに関係なく非常に高速に,つまり “O(1)” の定数時間で行われます.実際, std::vector などの構造体はコピーコンストラクタと割り当て演算子を提供しますが,データ構造体が大きい場合この処理には無視できない時間がかかります.しかし,その構造体が Ptr<> でラッピングされていれば,データサイズとは関係なく小さいオーバーヘッドで済みます.
- C の構造体でも自動的にデストラクションが可能になります.以下の FILE* を用いた例を参照してください.
- 異種オブジェクトのコレクションが実現できます.標準の STL,他の多くの C++ や OpenCV のコンテナは,同じ型,同じサイズのオブジェクトしか格納することができません.異なる型のオブジェクトを同じコンテナに収める古典的な方法は,代わりに基底クラス base_class_t* のポインタを格納することですが,それは自動的なメモリ管理を諦めることになります.ここで再び,単純なポインタの代わりに Ptr<base_class_t>() を利用することで,この問題を解決できます.
Ptr クラスは,ラッピングされたオブジェクトをブラックボックスとして扱います.参照カウンタは個別に確保,管理されます.ポインタクラスが知っておく必要があるのは,オブジェクトの解放の方法だけです.それは, Ptr::delete_obj() メソッドにカプセル化され,参照カウンタが 0 になったときに呼ばれます.このメソッドはデフォルトで delete obj; を呼ぶので,オブジェクトが C++ のクラスインスタンスである場合は,追加のコーディングは必要ありません. しかし,オブジェクトが別の方法で解放される場合は,専用のメソッドを作る必要があります.例えば, FILE をラッピングしたい場合は, delete_obj を以下のような感じで実装します:
template<> inline void Ptr<FILE>::delete_obj()
{
fclose(obj); // さらにポインタをクリアする必要はありません.
// その処理,この外側で行われます.
}
...
// 使い方
Ptr<FILE> f(fopen("myfile.txt", "r"));
if(f.empty())
throw ...;
fprintf(f, ....);
...
// Ptr<FILE> のデストラクタによって, FILE は自動的に閉じられます.
注意 :参照のインクリメント/デクリメント処理は,不可分な処理として実装されているので,このクラスをマルチスレッドアプリケーションで利用しても通常は安全です.また,参照カウンタを利用する Mat() やその他の OpenCV のクラスも同様です.
Mat¶
OpenCV C++ の n-次元の密な配列クラス.
class CV_EXPORTS Mat
{
public:
// ... 大量のメソッド ...
...
/*! 複数のビットフィールドを含みます:
- マジックシグネチャ
- 連続性フラグ
- ビット深度
- チャンネル数
*/
int flags;
//! 配列の次元 >= 2
int dims;
//! 行数および列数.配列が 2 次元以上の場合は (-1, -1) となります.
int rows, cols;
//! データを指すポインタ
uchar* data;
//! 参照カウンタを指すポインタ.
// ユーザが確保したデータを指す配列の場合,このポインタは NULL になります.
int* refcount;
// その他のメンバ
...
};
クラス
Mat
は,シングルチャンネル,またはマルチチャンネルの,密な n-次元数値配列です.実数,複素数値のベクトルや行列,グレースケール画像,カラー画像,ボクセルボリューム,ベクトル場,ポイントクラウド,テンソル,ヒストグラム(ただし,超高次元ヒストグラムの場合は,
SparseMat
の方が適しているかもしれません)などを格納するのに利用されます.
配列
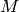 のデータレイアウトは,配列
M.step[]
によって定義され,要素
のデータレイアウトは,配列
M.step[]
によって定義され,要素
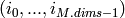 (ここで,
(ここで,
![0\leq i_k<M.size[k]](_images/math/234967a3ae0f8f42e43a5094139356e98c8c73a6.png) )のアドレスは次のように求められます:
)のアドレスは次のように求められます:
![addr(M_{i_0,...,i_{M.dims-1}}) = M.data + M.step[0]*i_0 + M.step[1]*i_1 + ... + M.step[M.dims-1]*i_{M.dims-1}](_images/math/29954d8c450a7ef8c777681a299e7e510c5c45e4.png)
2 次元配列の場合は,上述の式は,次のように簡略化できます:
![addr(M_{i,j}) = M.data + M.step[0]*i + M.step[1]*j](_images/math/d4118caa7595854a43554ec37d73da6eb1bbf4e3.png)
また, M.step[i] >= M.step[i+1] (実際は, M.step[i] >= M.step[i+1]*M.size[i+1] )であることに注意してください. つまり,2 次元の行列は行毎に格納され,3 次元の行列は平面毎に格納される,という風になっています. M.step[M.dims-1] が最小で,これは常に要素サイズ M.elemSize() と一致します.
これは, Mat のデータレイアウトが, OpenCV 1.x の CvMat , IplImage および CvMatND と完全に互換性があることを意味します.Numpy (ndarray),Win32 (device independent bitmap) などの標準的なツールキットやSDKの密な配列型,つまり,ピクセルの位置を計算するために “steps” (別名 “strides”)を利用する任意の配列に対しても同様です.この互換性により,ユーザが確保したデータに対する Mat ヘッダを作成し,OpenCV の関数を用いて,その値を置換しながら処理することが可能になります.
Mat オブジェクトを作成する方法はたくさんありますが,ここではポピュラーなものをいくつか示します:
create(nrows, ncols, type) メソッドや,それと同様のコンストラクタ Mat(nrows, ncols, type[, fillValue]) を利用します.
指定されたサイズ,型の新しい配列が確保されます. ここで
type は, cvCreateMat の場合と同じ意味を持ちます.
例えば,
CV_8UC1 は 8 ビットでシングルチャンネルの行列,
CV_32FC2 は 2 チャンネル(つまり複素数)浮動小数点型の配列を表します.
// 1+3j で埋められた 7x7 の複素行列を作成します. cv::Mat M(7,7,CV_32FC2,Scalar(1,3)); // そして, M を 100x60 で 15 チャンネル 8 ビットの行列に変更します. // 行列の以前の内容は解放されます. M.create(100,60,CV_8UC(15));
この章のイントロダクションでも述べたように, create() は,現在の配列の形状や型が指定されたものと異なる場合のみ,新しい行列を確保します.
similarly to above, you can create a multi-dimensional array:
// 100x100x100 で 8 ビットの配列を作成します. int sz[] = {100, 100, 100}; cv::Mat bigCube(3, sz, CV_8U, Scalar::all(0));
Mat コンストラクタに次元数 =1 が渡された場合でも,列数が 1 に設定された 2 次元の配列が作成されることに注意してください.これが, Mat::dims が常に >=2 (配列が空の場合は 0 にもなり得ます)である理由です.
コンストラクタや代入演算子を利用します.この場合,右辺は配列か matrix expression になります.詳しくは以下を参照してください.同じくイントロダクションで述べたように,配列の代入はヘッダをコピーして参照カウンタを増加させるだけなので O(1) の処理です.必要なときには Mat::clone() メソッドを使って,配列の完全なコピー(つまり,深いコピー)を得ることができます.
別の配列の一部分に対するヘッダを作成します.これは,配列の 1 行や 1 列,複数行や複数列,矩形領域(代数では小行列式と呼ばれます),対角要素などに対して可能です.新しいヘッダも同じデータを参照するので,この様な処理も O(1) です.この特徴を利用すると,例えば以下のように,配列の一部を実際に変更することができます.
// 5 行目 を 3 倍して, 3 行目に足します. M.row(3) = M.row(3) + M.row(5)*3; // 7 列目を 1 列目にコピーします. // M.col(1) = M.col(7); // これは動作しません Mat M1 = M.col(1); M.col(7).copyTo(M1); // 新たに 320x240 の画像を作成します. cv::Mat img(Size(320,240),CV_8UC3); // ROI を選択します. cv::Mat roi(img, Rect(10,10,100,100)); // ROI を (0,255,0) ( RGB 空間での緑)で埋めます. // 320x240 の元の画像は変更されます. roi = Scalar(0,255,0);
datastart および dataend メソッドが追加されたおかげで, locateROI() を用いてメインの “コンテナ” 配列内の部分配列の相対位置を計算することができます.
Mat A = Mat::eye(10, 10, CV_32S); // 1 列目(範囲に含む)から 3 列目(含まない)までを A として抽出します Mat B = A(Range::all(), Range(1, 3)); // 5 行目(範囲に含む)から 9 行目(含まない)までを B として抽出します // つまり, C ~ A(Range(5, 9), Range(1, 3)) Mat C = B(Range(5, 9), Range::all()); Size size; Point ofs; C.locateROI(size, ofs); // サイズは (width=10,height=10) , ofs は (x=1, y=5)
行列全体の場合と同様に,深いコピーが必要ならば,抽出された部分行列の clone() メソッドを利用します.
ユーザが確保したデータに対するヘッダを作成します.これは,以下の場合に有用です:
- OpenCVを用いた「別の」データの処理
(例えば, DirectShow のフィルタや, gstreamer の処理モジュールなどを実装する場合)
void process_video_frame(const unsigned char* pixels, int width, int height, int step) { cv::Mat img(height, width, CV_8UC3, pixels, step); cv::GaussianBlur(img, img, cv::Size(7,7), 1.5, 1.5); }
小さい行列の手軽な初期化 および/または 超高速な要素アクセス
double m[3][3] = {{a, b, c}, {d, e, f}, {g, h, i}}; cv::Mat M = cv::Mat(3, 3, CV_64F, m).inv();
このように「ユーザが確保したデータに対するヘッダを作成する」場合, CvMat や IplImage から Mat への変換が,非常に頻繁に行われる事があります.このために, CvMat や IplImage へのポインタをとる専用のコンストラクタと,データをコピーするか否かを指定するオプションフラグが存在します.
また,
Mat から CvMat や IplImage への後方変換は,キャスト演算子 Mat::operator CvMat() const と Mat::operator IplImage() によって提供されます.この演算子は,データをコピー しません .
IplImage* img = cvLoadImage("greatwave.jpg", 1); Mat mtx(img); // IplImage* -> cv::Mat の変換 CvMat oldmat = mtx; // cv::Mat -> CvMat の変換 CV_Assert(oldmat.cols == img->width && oldmat.rows == img->height && oldmat.data.ptr == (uchar*)img->imageData && oldmat.step == img->widthStep);
MATLAB 形式 zeros(), ones(), eye() の配列初期化,つまり:
// 倍精度の単位行列を作成して,それを M に足します. M += Mat::eye(M.rows, M.cols, CV_64F);
カンマ区切りの初期化子:
// 3x3 の倍精度単位行列を作成します. Mat M = (Mat_<double>(3,3) << 1, 0, 0, 0, 1, 0, 0, 0, 1);
ここでは,まず(後で述べる) Mat_ クラスのコンストラクタに適切なパラメータを与えて呼び出し,さらに << 演算子に続いて,定数,変数,式などから成るカンマ区切りの値を与えています.また,コンパイルエラーを避けるために,カッコが必要なことにも注意してください.
一度作成された配列は,参照カウント機構により自動的に管理されます(ただし,ユーザが確保したデータに対して配列ヘッダが作成される場合を除きます.この場合,ユーザ自身がデータを処理しなければいけません). 配列データは,それを指し示すものがなくなった場合に解放されます.配列のデストラクタが呼ばれるよりも前に,その配列ヘッダによって指されるデータを解放したい場合は, Mat::release() を利用してください.
配列クラスに関して次に学ぶ重要事項は,要素へのアクセスです.各配列要素のアドレスを計算する方法は既に述べました.通常は,コード内でその式を直接使う必要はありません.配列の型(
Mat::type()
メソッドを利用して得ることができます)が既知ならば,次のようにして 2 次元配列の要素
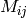 にアクセスすることができます:
にアクセスすることができます:
M.at<double>(i,j) += 1.f;
ここでは, M が倍精度の浮動小数点型配列だと仮定しています.また,異なる次元数に対応する複数の at メソッドが用意されています.
行列の行全体を処理する必要がある場合に最も効率的な方法は,最初の行のポインタを取得して,純粋な C 言語の演算子 [] を利用することです:
// 値が正である要素の合計を求めます.
// (ここで M は倍精度行列と仮定します)
double sum=0;
for(int i = 0; i < M.rows; i++)
{
const double* Mi = M.ptr<double>(i);
for(int j = 0; j < M.cols; j++)
sum += std::max(Mi[j], 0.);
}
上述のような処理は,実際は配列の形には依存せず,配列要素を 1 つ 1 つ処理する(または,配列同士の足し算のように,複数の配列の同じ座標にある要素を処理する)だけです.このような処理は要素ワイズと呼ばれ,すべての入出力配列が連続であるか,つまり,各行末にギャップが存在しないかどうかをチェックするのが常套手段です.もしそうならば,長く続く 1 つの行であるかのように処理できます.
// 値が正である要素の合計を求めます,最適化版
double sum=0;
int cols = M.cols, rows = M.rows;
if(M.isContinuous())
{
cols *= rows;
rows = 1;
}
for(int i = 0; i < rows; i++)
{
const double* Mi = M.ptr<double>(i);
for(int j = 0; j < cols; j++)
sum += std::max(Mi[j], 0.);
}
値が連続する行列の場合,外側のループは 1 回だけ実行されるのでオーバーヘッドが小さくなります.これは,特に小さい行列の場合に顕著です.
最後に,行と行の間のギャップをスキップする STL 形式の優れたイテレータの例を述べます:
// 値が正である要素の合計を求める,イテレータ利用版
double sum=0;
MatConstIterator_<double> it = M.begin<double>(), it_end = M.end<double>();
for(; it != it_end; ++it)
sum += std::max(*it, 0.);
行列のイテレータは,ランダムアクセスイテレータなので, std::sort() を含むすべての STL アルゴリズムに適用できます.
Matrix Expressions¶
これは,実装されている行列演算の一覧であり,組み合わせて任意の複雑な表現を行うこともできます(ここで
A
と
B
は行列を表し,
s
はスカラ(
Scalar
)を,
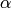 は実数値のスカラ(
double
)を表します).
は実数値のスカラ(
double
)を表します).
加算,減算,符号反転:
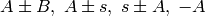
スケーリング:
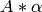 ,
,
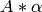
要素毎の積,商:
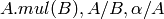
行列の積:
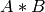
転置:
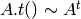
逆行列,擬似逆行列,連立方程式,最小二乗問題の解:
![A.inv([method]) \sim A^{-1}, A.inv([method])*B \sim X:\,AX=B](_images/math/d23defd775e709bb2e37362865fe14e81abc4a7a.png)
比較:
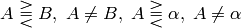 .
.比較結果は,8 ビットのシングルチャンネルマスクで,(特定の要素,あるいは要素の組が条件を満たしていれば)255 か,(そうでなければ)0 にセットされます.
ビット単位の論理演算: A & B, A & s, A | B, A | s, A textasciicircum B, A textasciicircum s, ~ A
要素単位の最小値,最大値:
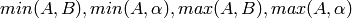
要素単位の絶対値:
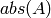
外積,内積:
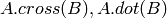
行列かスカラを返す,行列,行列同士,スカラに対するあらゆる演算.例えば,
norm() , mean() , sum() , countNonZero() , trace() ,
determinant() , repeat() など.
行列の初期化子( eye(), zeros(), ones() ),行列のカンマ区切り初期化子,行列コンストラクタ,部分行列を抽出する演算子( Mat() の説明を参照してください).
結果を適切な型に変換するための verb “Mat_<destination_type>()” コンストラクタ.
また,カンマ区切りの初期化子,あるいはその他の演算は,曖昧さを回避するために明示的に Mat() や verb “Mat_<T>()” コンストラクタを呼び出す必要があるかもしれない事に注意してください.
以下は, Mat のメソッドの正式な説明です.
cv::Mat::Mat¶
- (1) Mat::Mat()
- (2) Mat::Mat(int rows, int cols, int type)
- (3) Mat::Mat(Size size, int type)
- (4) Mat::Mat(int rows, int cols, int type, const Scalar& s)
- (5) Mat::Mat(Size size, int type, const Scalar& s)
- (6) Mat::Mat(const Mat& m)
- (7) Mat::Mat(int rows, int cols, int type, void* data, size_t step=AUTO_STEP)
- (8) Mat::Mat(Size size, int type, void* data, size_t step=AUTO_STEP)
- (9) Mat::Mat(const Mat& m, const Range& rowRange, const Range& colRange)
- (10) Mat::Mat(const Mat& m, const Rect& roi)
- (11) Mat::Mat(const CvMat* m, bool copyData=false)
- (12) Mat::Mat(const IplImage* img, bool copyData=false)
- (13) template<typename T, int n> explicit Mat::Mat(const Vec<T, n>& vec, bool copyData=true)
- (14) template<typename T, int m, int n> explicit Mat::Mat(const Matx<T, m, n>& vec, bool copyData=true)
- (15) template<typename T> explicit Mat::Mat(const vector<T>& vec, bool copyData=false)
- (16) Mat::Mat(const MatExpr& expr)
- (17) Mat::Mat(int ndims, const int* sizes, int type)
- (18) Mat::Mat(int ndims, const int* sizes, int type, const Scalar& s)
- (19) Mat::Mat(int ndims, const int* sizes, int type, void* data, const size_t* steps=0)
- (20) Mat::Mat(const Mat& m, const Range* ranges)
様々な行列コンストラクタ.
パラメタ: - ndims – 配列の次元数.
- rows – 2 次元配列における行数.
- cols – 2 次元配列における列数.
- size – 2 次元配列のサイズ: Size(cols, rows) . Size() コンストラクタでは,行数と列数が逆順になっていることに注意してください.
- sizes – n-次元配列の形状を表す,整数型の配列.
- type – 配列の型.1-4 チャンネルの行列を作成するには CV_8UC1, ..., CV_64FC4 を,マルチチャンネル(最大で CV_MAX_CN チャンネル)の行列を作成するには, CV_8UC(n), ..., CV_64FC(n) を利用してください.
- s – 各行列要素を初期化するオプション値.すべての行列要素を特定の値にセットするには,コンストラクタの後で,代入演算子 Mat::operator=(const Scalar& value) を利用してください.
- data – ユーザデータへのポインタ. data と step パラメータを引数にとる行列コンストラクタは,行列データ領域を確保しません.代わりに,指定のデータを指し示す行列ヘッダを初期化します.つまり,データのコピーは行われません.この処理は,非常に効率的で,OpenCV の関数を利用して外部データを処理することができます.外部データが自動的に解放されることはありませんので,ユーザが解放する必要があります.
- step – The data buddy. このオプションパラメータでは,行列の各行が占めるバイト数を指定できます.この値は,各行の終端にパディングバイトが存在すれば,それも含みます.このパラメータが指定されない場合( cv::AUTO_STEP にセットされて),パディングは存在しないとみなされ,実際の step は cols*elemSize() として計算されます. Mat::elemSize () を参照してください.
- steps – 多次元配列における ndims-1 個のステップを表す配列(最後のステップは常に要素サイズになります).これが指定されないと,行列は連続したものとみなされます.
- m – 作成された行列に(全体的,部分的に)割り当てられる配列.これらのコンストラクタによってデータがコピーされる事はありません.代わりに,データ m ,またはその部分配列を指し示すヘッダが作成され,関連した参照カウンタがあれば,それがインクリメントされます.つまり,新しく作成された配列の内容を変更することで, m の対応する要素も変更することになります.もし部分配列の独立したコピーが必要ならば, Mat::clone() を利用してください.
- img – 古い形式である IplImage 画像構造体へのポインタ.デフォルトでは,元の画像と新しい行列とでデータが共有されますが, copyData フラグがセットされている場合は,画像データの完全なコピーが作成されます.
- vec – STL vector .このベクトルの要素が行列の要素になります.行列は,単一の列と,vector の要素と同じ数の行を持ちます.また,行列の型は,vector の要素の型と一致します.コンストラクタは,適切に宣言された DataType が存在する任意の型を扱うことが可能です.つまり,vector の要素は必ず,プリミティブな数値か,単一の型の数値タプルでなければいけません.当然,型が混在する構造体はサポートされません.また,対応するコンストラクタは明示する必要がある事に注意してください.つまり,STL vector が自動的に Mat インスタンスに変換されることはなく, Mat(vec) を明示的に記述しなければいけません.行列にデータをコピーする( copyData=true )場合を除いて,vector に新たに要素を追加するべきではありません.なぜなら,それによって vector データの再配置が発生する可能性があり,行列データポインタが無効になるからです.
- copyData – STL vector の内部データ,古い形式の CvMat または IplImage を新しく作成される行列にコピーする(true)か,共有する(false)かを指定するフラグです.データがコピーされる場合,確保されたバッファは Mat の参照カウント機構を用いて管理されます.データが共有される場合,参照カウンタは NULL になり,ユーザは,作成された行列がデストラクトされない限り,データを解放するべきではありません.
- rowRange – 扱われる m の行の範囲.すべての行を扱う場合は, Range::all() を利用してください.
- colRange – 扱われる m の列の範囲.すべての列を扱う場合は, Range::all() を利用してください.
- ranges – m の各次元毎の選択範囲を表す配列.
- expr – Matrix expression. Matrix Expressions を参照してください.
これらは,行列を作成するための様々なコンストラクタです. イントロダクション の注意書きにもあるように,多くの場合はデフォルトコンストラクタで十分であり,OpenCV の関数により適切な行列が確保されます.作成された行列は,さらに別の行列や matrix expression に代入することができ,その場合,古い内容に対しては参照外しが行われます.あるいは,行列をさらに Mat::create によって確保することもできます.
cv::Mat::Mat¶
行列のデストラクタは Mat::release を呼び出します.
cv::Mat::operator =¶
- Mat& Mat::operator = (const Mat& m)
- Mat& Mat::operator = (const MatExpr_Base& expr)
- Mat& operator = (const Scalar& s)
行列の代入演算子.
パラメタ: - m – 代入される,右辺の行列.行列の代入は O(1) の処理であり,つまりデータのコピーは行われません.その代わり,参照カウンタがあれば,それがインクリメントされます.また,新しいデータを代入する前に, Mat::release によって古いデータの参照外しが行われます.
- expr – 代入される matrix expression オブジェクト.代入演算の第 1 の形式とは逆に,この第 2 の形式では,matrix expression と一致するサイズと型を持っていれば,既に確保された行列を再利用することが可能です.これは,実際の関数に展開された matrix expression によって自動的に扱われます.例えば, C=A+B は cv::add(A, B, C) に展開され,この add() は,自動的に C の再確保を行います.
- s – 各行列要素に代入されるスカラ.行列サイズや型は変更されません.
これらは,すべて有効な代入演算子です.それぞれがまったく違う形式なので,演算子の説明をきちんと読んでください.
cv::Mat::operator MatExpr¶
- Mat::operator MatExpr_<Mat, Mat>() const
行列から MatExpr へのキャスト演算子.
このキャスト演算子は,明示的に呼ばれるべきものではありません. Matrix Expressions エンジンで,内部的に利用されます.
cv::Mat::row¶
このメソッドは,行列の指定行に対する新しいヘッダを作成し,それを返します.これは,行列のサイズにかかわらず O(1) の処理です.新しい行列の内部データは,元の行列と共有されます.ここでは,LU やその他たくさんのアルゴリズムで利用されている,古典的で基本的な行列処理の 1つ である axpy の例を紹介します.
inline void matrix_axpy(Mat& A, int i, int j, double alpha)
{
A.row(i) += A.row(j)*alpha;
}
重大な注意 .現在の実装では,以下のコードは期待通りには動作しません.
Mat A;
...
A.row(i) = A.row(j); // 動作しません
動作しない理由は, A.row(i) が一時的なヘッダを作成し,そこにさらに別のヘッダに代入されるからです.これらの演算子は O(1) ,つまりデータのコピーは行われないことを忘れないでください.従って,j 番目の行が i 番目の行にコピーされると期待して上述の代入を行っても,期待通りには動きません.それを行うには,単純な代入を expression を利用したものに代えるか, Mat::copyTo メソッドを利用するかしてください.
Mat A;
...
// 動作しますが,少し分かり難いです.
A.row(i) = A.row(j) + 0;
// すこし長いですが,おすすめの方法です.
Mat Ai = A.row(i); M.row(j).copyTo(Ai);
cv::Mat::col¶
このメソッドは,行列の指定列に対する新しいヘッダを作成し,それを返します.これは,行列のサイズにかかわらず O(1) の処理です.新しい行列の内部データは,元の行列と共有されます. Mat::row の説明も参照してください.
cv::Mat::rowRange¶
- Mat Mat::rowRange(const Range& r) const
行列の指定された範囲行に対する行列ヘッダを作成します.
パラメタ: - startrow – 範囲行の先頭インデックス.0 基準.
- endrow – 範囲行の末尾インデックス.0 基準.
- r – インデックスの先頭と末尾を共に含む Range() 構造体.
このメソッドは,行列の指定範囲行に対する新しいヘッダを作成します.これは Mat::row() や Mat::col() と同様に,O(1) の処理です.
cv::Mat::colRange¶
- Mat Mat::colRange(const Range& r) const
行列の指定された範囲列に対する行列ヘッダを作成します.
パラメタ: - startrow – 範囲行の先頭インデックス.0 基準.
- endrow – 範囲行の末尾インデックス.0 基準.
- r – 先頭および末尾インデックスを共に含む Range() 構造体.
このメソッドは,行列の指定範囲行に対する新しいヘッダを作成します.これは Mat::row() や Mat::col() と同様に,O(1) の処理です.
cv::Mat::diag¶
- Mat Mat::diag(int d) const static Mat Mat::diag(const Mat& matD)¶
行列から対角成分を抜き出します.または対角行列を作成します.
パラメタ: - d –
以下を意味する,対角成分のインデックス.
- d=0 主対角成分.
- d>0 主対角成分の下側の対角成分.例えば d=1 は,主対角成分の 1 つ下の対角成分を意味します.
- d<0 主対角成分の上側の対角成分.例えば d=-1 は,主対角成分の 1 つ上の対角成分を意味します.
- matD – 1 列の行列.ここから対角行列を構成します.
- d –
このメソッドは,指定された行列の対角成分に対する新しいヘッダを作成します.この新しい行列は,1 列の行列として表現されます. Mat::row() や Mat::col() と同様に,これも O(1) の処理です.
cv::Mat::clone¶
このメソッドは,配列の完全なコピーを作成します.しかし,元の step[] は考慮されません.つまり,この配列コピーは,連続した total()*elemSize() バイトの領域を占有します.
cv::Mat::copyTo¶
- void Mat::copyTo(Mat& m ) const void Mat::copyTo( Mat& m, const Mat& mask) const¶
行列を別の行列にコピーします.
パラメタ: - m – コピー先の行列.適切なサイズ,型ではない場合は,処理の前に再割り当てされます.
- mask – 処理マスク.この非ゼロの要素が,コピーするべき行列の要素を表します.
このメソッドは,行列のデータを別の行列にコピーします.データをコピーする前に,このメソッドは以下を呼び出します.
m.create(this->size(), this->type);
これにより,必要ならばコピー先の行列が再割り当てされます. m.copyTo(m); は期待通りの動作になり,つまり,行列は何も変化しません.しかし一方で,コピー元とコピー先の行列が部分的にオーバラップするような場合は,この関数では扱うことはできません.
処理マスクが指定される場合,そして,上述の Mat::create 呼び出しが行列を再割り当てする場合,新しく確保された行列は,データコピーの前に 0 で初期化されます.
cv::Mat::convertTo¶
- void Mat::convertTo(Mat& m, int rtype, double alpha=1, double beta=0) const¶
配列のデータを別の型に変換します.オプションで,スケーリングか可能です.
パラメタ: - m – 出力行列.適切なサイズ,型ではない場合は,処理の前に再配置されます.
- rtype – 出力行列に要求する型,(チャンネル数は元の行列と同じなので)正確には,要求するビット深度,になります. rtype が負の場合は,出力行列は元の行列と同じ型になります.
- alpha – オプションのスケールファクタ.
- beta – オプションのデルタ.スケーリングされた値に足されます.
このメソッドは,元行列のピクセル値を目的のデータ型に変換します.オーバフローを回避するために,処理の最後に saturate_cast<> が適用されます.
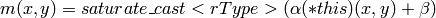
cv::Mat::assignTo¶
- void Mat::assignTo(Mat& m, int type=-1) const¶
convertTo の関数形式.
パラメタ: - m – 出力配列.
- type – 出力配列のビット深度(-1 の場合は元の行列と同じであることを意味します).
これは, Matrix Expressions エンジンによって内部的に利用されるメソッドです.
cv::Mat::setTo¶
- Mat& Mat::setTo(const Scalar& s, const Mat& mask=Mat())¶
すべて,またはいくつかの配列の要素に,指定された値をセットします.
パラメタ: - s – 代入されるスカラー値.これは,実際の配列の型に変換されます.
- mask – *this と同じサイズの処理マスク.
これは, Mat::operator=(const Scalar& s) 演算子の詳細版です.
cv::Mat::reshape¶
- Mat Mat::reshape(int cn, int rows=0) const¶
データをコピーすることなく,2 次元の行列の形状かチャンネル数,あるいはその両方を変更します.
パラメタ: - cn – 新しいチャンネル数.このパラメータが 0 の場合,チャンネル数はそのままになります.
- rows – 新しい行数.このパラメータが 0 の場合,行数はそのままになります.
このメソッドは, *this 要素に対する新しい行列ヘッダを作成します.新しい行列は,元の行列とは,サイズかチャンネル数,あるいはその両方が異なります.以下の条件内であれば,どのような組み合わせも可能です.
- 新しい行列に要素が追加されたり,逆に削除されたりしません.その結果, rows*cols*channels() は変換後も同じ値になります.
- データはコピーされません.つまり,これは O(1) の処理です.その結果,行数を変更したり,何か他の方法で要素の行インデックスを変更したりしても,行列のデータ領域は連続となります.
ここでは,簡単な例を示します.STL vector に保存された 3 次元の点群があり,これを 3xN の行列で表現したいとします.その処理は,次のようになります:
std::vector<cv::Point3f> vec;
...
Mat pointMat = Mat(vec). // vector から Mat への変換. O(1) の処理です.
reshape(1). // Nx1 で 3 チャンネル行列から, Nx3 で 1 チャンネル行列を作成します.
// これも O(1) の処理です.
t(); // 最後に, Nx3 の行列を転置します.
// これは,全要素のデータコピーを含みます.
cv::Mat::t¶
- MatExpr Mat::t() const¶
行列の転置を行います.
このメソッドは, matrix expressions を用いて行列の転置を行います. 実際に転置を行うわけではなく,一時的な “転置行列” オブジェクトを返します.これは,より複雑な行列表現の一部として利用したり,ある行列に代入したりすることができます.
Mat A1 = A + Mat::eye(A.size(), A.type)*lambda;
Mat C = A1.t()*A1; // (A + lambda*I)^t * (A + lamda*I) を計算します
cv::Mat::inv¶
- MatExpr Mat::inv(int method=DECOMP_LU) const¶
逆行列を求めます.
パラメタ: - method –
逆行列を求める方法.以下のうちの1つ.
- DECOMP_LU LU 分解.行列は,非特異行列でなければいけません.
- DECOMP_CHOLESKY コレスキー
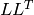 分解.利用できるのは,正定値対称行列のみです.巨大な行列に対しては,LU 分解の約 2 倍高速です.
分解.利用できるのは,正定値対称行列のみです.巨大な行列に対しては,LU 分解の約 2 倍高速です. - DECOMP_SVD 特異値分解.行列は,特異または非正方でも構いませんが,その場合擬似逆行列が計算されます.
- method –
このメソッドは,matrix expression を用いて逆行列を計算します.つまりこのメソッドは,より複雑な matrix expression の一部として利用したり,行列に代入したりすることが可能な,一時的な「逆行列」オブジェクトを返します.
cv::Mat::mul¶
- MatExpr Mat::mul(const MatExpr& m, double scale=1) const
2 つの行列の要素同士の掛け算,割り算を行います.
パラメタ: - m – *this と同じ型,同じサイズの別の行列,または matrix expression です.
- scale – オプションのスケールファクタ.
このメソッドは,配列の要素同士の掛け算+オプションとしてのスケーリング,を表す一時的なオブジェクトを返します.これは,単純な “*” 演算子に対応する行列同士の積とは異なることに注意してください.
ここで例を示します:
Mat C = A.mul(5/B); // divide(A, B, C, 5) と等価です.
cv::Mat::cross¶
このメソッドは,3 要素ベクトル同士の外積を計算します.この,ベクトルは同じ形状,同じサイズの 3 要素浮動小数点型ベクトルでなければいけません.計算結果は,入力ベクトルと同じ形状,同じ型の,別の 3 要素ベクトルとなります.
cv::Mat::dot¶
このメソッドは,2 つの行列同士の内積を計算します.行列が 1 行または 1 列の行列でなかった場合,上から下,左から右の順番でスキャンを行い,それぞれを 1 次元ベクトルとして扱います.これらの 2 つベクトルは,同じサイズ,同じ型でなければいけません.行列が 2 つ以上のチャンネルを持つ場合,各チャンネルでの内積が足し合わされます.
cv::Mat::zeros¶
- static MatExpr Mat::zeros(int rows, int cols, int type) static MatExpr Mat::zeros(Size size, int type) static MatExpr Mat::zeros(int ndims, const int* sizes, int type)¶
指定されたサイズ,型の零配列を返します.
パラメタ: - ndims – 配列の次元数.
- rows – 行数.
- cols – 列数.
- size – 行列サイズ指定の別の表現: Size(cols, rows) .
- sizes – 配列の形状を表す,整数型の配列.
- type – 作成される行列の型.
このメソッドは,Matlab 形式の,配列を 0 で埋めるイニシャライザを返します.これは,定数配列を作成する簡単な書式で,関数のパラメータ,matrix expression の一部,行列イニシャライザとして利用可能です.
Mat A;
A = Mat::zeros(3, 3, CV_32F);
上述のサンプルでは, A が 3x3 の浮動小数点型行列ではない場合にのみ,新しい行列が確保されます.それ以外の場合は,既に存在する行列 A が 0 で埋められます.
cv::Mat::ones¶
- static MatExpr Mat::ones(int rows, int cols, int type) static MatExpr Mat::ones(Size size, int type) static MatExpr Mat::ones(int ndims, const int* sizes, int type)¶
指定されたサイズ,型で,すべての要素が 1 である配列を返します.
パラメタ: - ndims – 配列の次元数.
- rows – 行数.
- cols – 列数.
- size – 行列サイズ指定の別の表現: Size(cols, rows) .
- sizes – 配列の形状を表す,整数型の配列.
- type – 作成される行列の型.
このメソッドは Mat::zeros() と同様に,Matlab 形式の,配列を 1 で埋めるイニシャライザを返します.このメソッドを利用する場合,以下の Matlab 表現を用いると,配列を任意の値で初期化できることに注意してください:
Mat A = Mat::ones(100, 100, CV_8U)*3; // 3 で埋められた 100x100 の行列.
上述の処理は,1 で埋められた 100x100 行列を作成して,それを 3 倍するわけではありません.行列イニシャライザを実際に呼び出す場合,スケールファクタ(この場合は 3 )を考慮して利用してください.
cv::Mat::eye¶
- static MatExpr Mat::eye(int rows, int cols, int type) static MatExpr Mat::eye(Size size, int type)¶
指定されたサイズ,型の単位行列を返します.
パラメタ: - rows – 行数.
- cols – 列数.
- size – 行列サイズ指定の別の表現: Size(cols, rows) .
- type – 作成される行列の型.
このメソッドは Mat::zeros() と同様に,Matlab 形式の単位行列イニシャライザを返します. Mat::ones の場合と同様に,スケール操作を行い,定数倍された単位行列を効率的に作成することができます:
// 対角要素が 0.1 である 4x4 の対角行列を作成します.
Mat A = Mat::eye(4, 4, CV_32F)*0.1;
cv::Mat::create¶
- void Mat::create(int rows, int cols, int type) void Mat::create(Size size, int type) void Mat::create(int ndims, const int* sizes, int type)¶
必要ならば,新しい配列データを確保します.
パラメタ: - ndims – 配列の次元数.
- rows – 行数.
- cols – 列数.
- size – 行列サイズ指定の別の表現: Size(cols, rows) .
- sizes – 配列の形状を表す,整数型の配列.
- type – 新しい行列の型.
これは, Mat の最重要メソッドの 1 つです.新形式の OpenCV 関数の中で,配列を作成するものの大部分は,各出力配列毎にこのメソッドを呼び出します.このメソッドのアルゴリズムは,次のようになります:
- 現在の配列形状と型が,新しい行列と一致する場合,即座に return します.
- そうでない場合, Mat::release() を呼び出して,以前のデータに対して参照外しを行います.
- 新しいヘッダを初期化します.
- total()*elemSize() バイトの新しいデータを確保します.
- データに関連付けられた新しい参照カウンタを作成し,その値を 1 にセットします.
ロバストかつ効率的なメモリ管理を同時に行うこのような機構は,ユーザのタイプ量を大きく削減します.つまり通常は,出力配列を明示的に確保する必要はない,という事です.
Mat color;
...
Mat gray(color.rows, color.cols, color.depth());
cvtColor(color, gray, CV_BGR2GRAY);
このように書く代わりに,次の用に簡単に記述できます:
Mat color;
...
Mat gray;
cvtColor(color, gray, CV_BGR2GRAY);
OpenCV の多くの関数と同様に, cvtColor も,内部で出力配列を作るために Mat::create() を呼び出すからです.
cv::Mat::addref¶
- void Mat::addref()¶
参照カウンタをインクリメントします.
このメソッドは,行列データに関連付けられた参照カウンタをインクリメントします.行列ヘッダが外部データを指し示している場合( Mat::Mat() を参照)は,参照カウンタは NULL です.その場合,このメソッドは何もしません.メモリリークを避けるため,通常このメソッドは明示的に呼ばれるべきではありません.行列の代入演算子においては,内部的に呼び出されています.また,参照カウンタの増加は,それをサポートするプラットフォーム上では不可分な操作なので,異なるスレッドで同じ行列を非同期に処理しても安全です.
cv::Mat::release¶
- void Mat::release()¶
参照カウンタをデクリメントし,必要ならば行列を解放します.
このメソッドは,行列データに関連付けられた参照カウンタをデクリメントします.参照カウンタが 0 になると,行列データは解放され,そのデータと参照カウンタのポインタは NULL にセットされます.行列ヘッダが外部データを指し示している場合( Mat::Mat() を参照)は,参照カウンタは NULL です.その場合,このメソッドは何もしません.
行列データを強制的に解放するために,このメソッドを手動で呼び出すことができます.しかし,デストラクタ,そしてデータポインタを変更するあらゆるメソッドは自動的にこのメソッドを呼び出すので,通常その必要はありません.参照カウンタの減少とそれが 0 に到達したかどうかのチェックは,それをサポートするプラットフォーム上では不可分な操作なので,異なるスレッドで同じ行列を非同期に処理しても安全です.
cv::Mat::resize¶
- void Mat::resize(size_t sz) const¶
行列の行数を変更します.
パラメタ: - sz – 新しい行数.
このメソッドは,行列の行数を変更します.行列が再割り当てされると,先頭の min(Mat::rows, sz) 行が保存されます.このメソッドは,STL vector クラスの同メソッドを模擬したものです.
Mat::push_back¶
- template<typename T> void Mat::push_back(const T& elem)¶
- template<typename T> void Mat::push_back(const Mat_<T>& elem)
行列の末尾に要素を追加します.
パラメタ: - elem – 追加されれる要素.
このメソッドは,1 つまたは複数の要素を行列の末尾に追加します.STL vector クラスの同メソッドを模擬したものです. elem が mat の場合,その型と列数が,追加される側の行列と同じでなければいけません.
Mat::pop_back¶
- template<typename T> void Mat::pop_back(size_t nelems=1)¶
行列の末尾の要素を削除します.
パラメタ: - nelems – 削除される行数.これが行の総数よりも大きい場合,例外が投げられます.
このメソッドは,1 つまたは複数の行を,行列の末尾から削除します.
cv::Mat::locateROI¶
- void Mat::locateROI(Size& wholeSize, Point& ofs) const¶
行列ヘッダが,親行列内のどこを指しているかを求めます.
パラメタ: - wholeSize – 行列全体のサイズが代入される出力パラメータ. *this は,これの一部となります.
- ofs – 出力パラメータ.行列全体の内側にある *this のオフセット値を表します.
Mat::row() , Mat::col() , Mat::rowRange() , Mat::colRange() などを利用して行列から部分行列を抽出した後,結果として得られる部分行列は元の大きな行列の一部を指し示すだけのものです.しかし,それぞれの部分行列は,( datastart と dataend フィールドによって表される)情報を持っています.これを用いることで,元の行列サイズと,抽出された部分行列が元の行列のどこに位置していたか,を復元できます.このメソッド locateROI は,まさにそれを行うものです.
cv::Mat::adjustROI¶
- Mat& Mat::adjustROI(int dtop, int dbottom, int dleft, int dright)¶
親行列内の部分行列のサイズと位置を調整します.
パラメタ: - dtop – 部分行列の上側の境界の,上への移動量.
- dbottom – 部分行列の下側の境界の,下への移動量.
- dleft – 部分行列の左側の境界の,左への移動量.
- dright – 部分行列の右側の境界の,右への移動量.
このメソッドは, Mat::locateROI() を補足するものです.実際,これらの関数の典型的な用法は,親行列内での部分行列の位置を検出して移動させる,というものです.ROI の外側のピクセルを考慮しなければならないフィルタリング処理は,このような処理が必要になる典型的な場合です.メソッドのすべてのパラメータは正値であり,これは,ROI がすべての方向に指定され量だけ増加しなければいけない,ということを意味します.つまり,以下の処理の場合:
A.adjustROI(2, 2, 2, 2);
これは,各方向に4要素分行列サイズを増加させ,それを2要素分だけ左と上に移動させます.これによって, 5x5 のカーネルでフィルタリングを行うために必要なすべてのピクセルを引き込むことになります.
adjustROI が親行列の境界を越えないようにするのはユーザの責任です.越えてしまった場合,この関数はエラー起こします.
この関数は, filter2D() やモルフォロジー演算などの,OpenCV のフィルタリング関数の内部で利用されています.
copyMakeBorder() も参照してください.
cv::Mat::operator()¶
- Mat Mat::operator()( const Rect& roi) const
- Mat Mat::operator()( const Ranges* ranges) const
矩形部分行列を抽出します.
パラメタ: - rowRange – 抽出された部分行列の最初と最後の行.最後の行は,範囲に含まれません.すべての行を選択するには, Range::all() を利用してください.
- colRange – 抽出された部分行列の最初と最後の列.最後の列は,範囲に含まれません.すべての列を選択するには, Range::all() を利用してください.
- roi – 抽出する部分行列を,矩形として指定したもの.
- ranges – 配列の各次元における,選択範囲内の配列.
この演算子は, *this 内部にある指定の部分配列に対する新しいヘッダを作成します.これらは, Mat::row() , Mat::col() , Mat::rowRange() そして Mat::colRange() の最も一般化された形式です.例えば, A(Range(0, 10), Range::all()) は, A.rowRange(0, 10) と等価です.前述したものと同様に,この演算子も O(1) の処理であり,データはコピーされません.
cv::Mat::operator CvMat¶
この演算子は,内部データをコピーせずに,行列に対する CvMat ヘッダを作成します.この処理では,参照カウンタは考慮されないので, CvMat ヘッダが利用されている間は,元の行列が解放されないようにしなければいけません.この演算子は,OpenCV の新旧の API を混合して利用している場合に役立ちます.例えば:
Mat img(Size(320, 240), CV_8UC3);
...
CvMat cvimg = img;
mycvOldFunc( &cvimg, ...);
ここで mycvOldFunc は,OpenCV 1.x のデータ構造を処理するための何らかの関数を表します.
cv::Mat::operator IplImage¶
この演算子は,内部データをコピーせずに,行列に対する IplImage ヘッダを作成します. IplImage ヘッダが利用されている間は,元の行列が解放されないようにしなければいけません. Mat::operator CvMat と同様に,この演算子は,OpenCV の新旧の API を混合して利用している場合に役立ちます.
cv::Mat::total¶
- size_t Mat::total() const¶
配列要素の総数を返します.
このメソッドは,配列要素の数(例えば,その配列が画像の場合は,ピクセルの数)を返します.
cv::Mat::isContinuous¶
- bool Mat::isContinuous() const¶
行列が連続であるか否かを調べます.
このメソッドは,行列の要素が連続して格納されていれば,つまり,各行の最後にギャップが存在しなければ true を返し,そうでなければ false を返します.明らかに, 1x1 や 1xN の行列は常に連続です. Mat::create() によって作成された行列は常に連続ですが, Mat::col() , Mat::diag() などによって部分行列が抜き出された場合,外部データに対して行列ヘッダが作成された場合などは,行列は連続とは限りません.
この連続性フラグは, Mat::flags フィールド内の 1 ビットとして保存され,行列ヘッダを作成する際に自動的に計算されます.したがって,連続性のチェックは非常に高速であり,理論的には,以下のような処理になります:
// Mat::isContinuous() の別の実装
bool myCheckMatContinuity(const Mat& m)
{
//(m.flags & Mat::CONTINUOUS_FLAG) != 0; を返します
return m.rows == 1 || m.step == m.cols*m.elemSize();
}
このメソッドは,非常に多くの OpenCV の関数で利用されており,同様にユーザも自由に利用できるものです.(算術演算,論理演算,数学関数,アルファブレンディング,色空間変換などの)要素毎の処理は,画像の幾何的特徴に依存しないので,すべての入出力配列が連続であれば,この関数は,それらを非常に長い 1 行のベクトルとして扱うことができる,という事が重要な部分です.ここでは,アルファブレンディング関数の実装方法を示します.
template<typename T>
void alphaBlendRGBA(const Mat& src1, const Mat& src2, Mat& dst)
{
const float alpha_scale = (float)std::numeric_limits<T>::max(),
inv_scale = 1.f/alpha_scale;
CV_Assert( src1.type() == src2.type() &&
src1.type() == CV_MAKETYPE(DataType<T>::depth, 4) &&
src1.size() == src2.size());
Size size = src1.size();
dst.create(size, src1.type());
// 配列の連続性チェックを行い,
// 連続だった場合,
// 配列を 1 次元ベクトルとして扱います.
if( src1.isContinuous() && src2.isContinuous() && dst.isContinuous() )
{
size.width *= size.height;
size.height = 1;
}
size.width *= 4;
for( int i = 0; i < size.height; i++ )
{
// 配列が連続の場合,
// 外側のループは 1 度しか実行されません.
const T* ptr1 = src1.ptr<T>(i);
const T* ptr2 = src2.ptr<T>(i);
T* dptr = dst.ptr<T>(i);
for( int j = 0; j < size.width; j += 4 )
{
float alpha = ptr1[j+3]*inv_scale, beta = ptr2[j+3]*inv_scale;
dptr[j] = saturate_cast<T>(ptr1[j]*alpha + ptr2[j]*beta);
dptr[j+1] = saturate_cast<T>(ptr1[j+1]*alpha + ptr2[j+1]*beta);
dptr[j+2] = saturate_cast<T>(ptr1[j+2]*alpha + ptr2[j+2]*beta);
dptr[j+3] = saturate_cast<T>((1 - (1-alpha)*(1-beta))*alpha_scale);
}
}
}
この技は非常に単純ですが,単純な要素処理を 10-20 パーセント高速化できます.特に,画像が比較的小さく,処理が非常に単純な場合に有効です.
そして,この関数では OpenCV のもう 1 つの慣用的手法を用いていることに注意してください.つまり,出力配列が適切なサイズと型であるかをチェックする代わりに Mat::create() を呼び出しています.また,新たに確保された配列は常に連続ですが, create() が常に新しい行列を確保するとは限らないので,出力配列をチェックします.
cv::Mat::elemSize¶
- size_t Mat::elemSize() const¶
行列の要素サイズをバイト単位で返します.
このメソッドは,行列の要素サイズをバイト単位で返します.例えば,行列の型が CV_16SC3 である場合,このメソッドは 3*sizeof(short) または 6 を返します.
cv::Mat::elemSize1¶
- size_t Mat::elemSize1() const¶
行列要素のチャンネル毎のサイズをバイト単位で返します.
このメソッドは,行列要素のチャンネル毎のサイズをバイト単位で返します.つまり,チャンネル数は無視されます.例えば,行列の型が CV_16SC3 である場合,このメソッドは sizeof(short) または 2 を返します.
cv::Mat::type¶
- int Mat::type() const¶
行列要素の型を返します.
このメソッドは, CV_16SC3 または 16 ビット符号あり整数,3 チャンネル配列 などの CvMat の型システムと互換性のある,行列要素の型を ID で返します.
cv::Mat::depth¶
- int Mat::depth() const¶
行列要素のビット深度を返します.
このメソッドは,行列要素のビット深度 ID ,つまり,各チャンネル毎の型を返します.例えば,16 ビット符号あり整数,3 チャンネル配列の場合,これは CV_16S を返します.行列の型の完全なリストは以下のとおりです:
- CV_8U - 8-ビット符号なし整数 ( 0..255 )
- CV_8S - 8-ビット符号あり整数 ( -128..127 )
- CV_16U - 16-ビット符号なし整数 ( 0..65535 )
- CV_16S - 16-ビット符号あり整数 ( -32768..32767 )
- CV_32S - 32-ビット符号あり整数 ( -2147483648..2147483647 )
- CV_32F - 32-ビット浮動小数点数 ( -FLT_MAX..FLT_MAX, INF, NAN )
- CV_64F - 64-ビット浮動小数点数 ( -DBL_MAX..DBL_MAX, INF, NAN )
cv::Mat::step1¶
- size_t Mat::step1() const¶
正規化された step を返します.
このメソッドは,行列の step を Mat::elemSize1() で割った値を返します.これは,行列の任意の要素に高速にアクセスするのに役立ちます.
cv::Mat::empty¶
- bool Mat::empty() const¶
配列が要素を持たない場合に true を返します.
このメソッドは, Mat::total() が 0 ,または Mat::data が NULL の場合に true を返します. pop_back() および resize() メソッドがあるので, M.total() == 0 の場合でも M.data == NULL とは限りません.
cv::Mat::ptr¶
- const uchar* Mat::ptr(int i=0) const
- template<typename _Tp> _Tp* Mat::ptr(int i=0)
- template<typename _Tp> const _Tp* Mat::ptr(int i=0) const
行列の指定された行へのポインタを返します.
パラメタ: - i – 0 基準の行インデックス.
このメソッドは,行列の指定行を指す uchar* ,または型付きポインタを返します.これらのメソッドの使用法の知るには, Mat::isContinuous() () 項にあるサンプルを参照してください.
cv::Mat::at¶
- template<typename T> T& Mat::at(int i) const¶
- template<typename T> const T& Mat::at(int i) const
- template<typename T> T& Mat::at(int i, int j)
- template<typename T> const T& Mat::at(int i, int j) const
- template<typename T> T& Mat::at(Point pt)
- template<typename T> const T& Mat::at(Point pt) const
- template<typename T> T& Mat::at(int i, int j, int k)
- template<typename T> const T& Mat::at(int i, int j, int k) const
- template<typename T> T& Mat::at(const int* idx)
- template<typename T> const T& Mat::at(const int* idx) const
指定された配列要素への参照を返します.
パラメタ: - j, k (i,) – それぞれ,0, 1, 2 次元におけるインデックス.
- pt – Point(j,i) という風に指定される要素位置.
- idx – 長さが Mat::dims のインデックス配列.
このテンプレートメソッドは,指定の配列要素への参照を返します.パフォーマンス向上のために,インデックスの範囲チェックは Debug モードでのみ行われます.
1 つのインデックス (i) をとるバージョンは,1 行または 1 列の 2 次元配列の要素にアクセスするために利用されます.つまり, A が 1 x N の浮動小数点型行列, B が M x 1 の整数型行列だとすると, A.at<float>(0,k+4) や B.at<int>(2*i+1,0) の代わりに, A.at<float>(k+4) や B.at<int>(2*i+1) と簡単に書くことができます.
ここでは,Hilbert 行列の初期化の例を示します:
Mat H(100, 100, CV_64F);
for(int i = 0; i < H.rows; i++)
for(int j = 0; j < H.cols; j++)
H.at<double>(i,j)=1./(i+j+1);
cv::Mat::begin¶
- template<typename _Tp> MatIterator_<_Tp> Mat::begin() template<typename _Tp> MatConstIterator_<_Tp> Mat::begin() const¶
行列の最初の要素を指した状態の,行列イテレータを返します.
このメソッドは,読み込み専用,または読み書き可能なイテレータを返します.行列イテレータの利用法は, STL の双方向イテレータの利用法に非常によく似ています.ここでは,行列イテレータを用いて書かれたアルファブレンディング関数を紹介します:
template<typename T>
void alphaBlendRGBA(const Mat& src1, const Mat& src2, Mat& dst)
{
typedef Vec<T, 4> VT;
const float alpha_scale = (float)std::numeric_limits<T>::max(),
inv_scale = 1.f/alpha_scale;
CV_Assert( src1.type() == src2.type() &&
src1.type() == DataType<VT>::type &&
src1.size() == src2.size());
Size size = src1.size();
dst.create(size, src1.type());
MatConstIterator_<VT> it1 = src1.begin<VT>(), it1_end = src1.end<VT>();
MatConstIterator_<VT> it2 = src2.begin<VT>();
MatIterator_<VT> dst_it = dst.begin<VT>();
for( ; it1 != it1_end; ++it1, ++it2, ++dst_it )
{
VT pix1 = *it1, pix2 = *it2;
float alpha = pix1[3]*inv_scale, beta = pix2[3]*inv_scale;
*dst_it = VT(saturate_cast<T>(pix1[0]*alpha + pix2[0]*beta),
saturate_cast<T>(pix1[1]*alpha + pix2[1]*beta),
saturate_cast<T>(pix1[2]*alpha + pix2[2]*beta),
saturate_cast<T>((1 - (1-alpha)*(1-beta))*alpha_scale));
}
}
cv::Mat::end¶
- template<typename _Tp> MatIterator_<_Tp> Mat::end() template<typename _Tp> MatConstIterator_<_Tp> Mat::end() const¶
行列の最後の要素の後ろを指した状態の,行列イテレータを返します.
このメソッドは,最後の行列要素の後ろを指すようにセットされた,読み込み専用,または読み書き可能なイテレータを返します.
Mat_¶
Mat() から派生する行列クラステンプレート.
template<typename _Tp> class Mat_ : public Mat
{
public:
// ... いくつかの固有のメソッド
// そして
// 追加のフィールドはありません
};
Mat_<_Tp> クラスは, Mat クラスに被せる「薄い」テンプレートラッパーです.追加のデータフィールドは一切なく,これも Mat も仮想メソッドをまったく持たないので,これら 2 つのクラスへの参照やポインタは,互いに自由に変換できます.しかし,そうする場合には注意が必要です.例えば:
// 100x100 , 8 ビットの行列を作成する
Mat M(100,100,CV_8U);
// これは,コンパイル可能です.データ変換は行われません.
Mat_<float>& M1 = (Mat_<float>&)M;
// プログラムは,以下の文でクラッシュします.
M1(99,99) = 1.f;
大抵の場合 Mat で十分ですが,要素アクセス演算子をたくさん利用し,コンパイル時に行列の型が分かっている場合は, Mat_ の方がより便利です. Mat::at<_Tp>(int y, int x) および Mat_<_Tp>::operator ()(int y, int x) は完全に等価で同じ速度で動作しますが,後者の方が確実に短く書けることに注意してください:
Mat_<double> M(20,20);
for(int i = 0; i < M.rows; i++)
for(int j = 0; j < M.cols; j++)
M(i,j) = 1./(i+j+1);
Mat E, V;
eigen(M,E,V);
cout << E.at<double>(0,0)/E.at<double>(M.rows-1,0);
マルチチャンネルの画像/行列の場合は ``Mat_`` をどうやって使うのでしょうか? これは簡単,つまり Vec を Mat_ のパラメータとして渡すだけです:
// 320x240 のカラー画像を確保して,( RGB 空間の)緑色で埋めます.
Mat_<Vec3b> img(240, 320, Vec3b(0,255,0));
// 対角線上に白い線を描きます.
for(int i = 0; i < 100; i++)
img(i,i)=Vec3b(255,255,255);
// 各ピクセルの 2 番目(赤)のチャンネルをスクランブルします.
for(int i = 0; i < img.rows; i++)
for(int j = 0; j < img.cols; j++)
img(i,j)[2] ^= (uchar)(i ^ j);
NAryMatIterator¶
n 変数の多次元配列イテレータ.
class CV_EXPORTS NAryMatIterator
{
public:
//! デフォルトコンストラクタ
NAryMatIterator();
//! 任意の個数の n 次元行列をとる,フルコンストラクタ
NAryMatIterator(const Mat** arrays, Mat* planes, int narrays=-1);
//! 分離されたイテレータの初期化メソッド
void init(const Mat** arrays, Mat* planes, int narrays=-1);
//! それぞれの反復行列の次の平面に進みます
NAryMatIterator& operator ++();
//! それぞれの反復行列の次の平面に進みます(後置インクリメント)
NAryMatIterator operator ++(int);
...
int nplanes; // 平面の総数
};
このクラスは,多次元配列における,1 変数,2 変数,そして一般的な n 変数の要素毎の処理を行うために利用されます.n 変数関数の引数に,連続した配列が含まれることがあるかもしれませんし,ないかもしれません.各配列に対して従来の MatIterator を使うことは可能ですが,個々の小さな処理の後で全てのイテレータをインクリメントするのは,非常に大きなオーバヘッドになります.そこで, NAryMatIterator の出番です.これを使うと,同じ形状(次元数が等しく,各次元のサイズも等しい)の複数の行列を同時に繰り返し処理することができます.各繰り返しにおいて, it.planes[0] , it.planes[1] は,対応する行列のスライスとなります.
ここでは例として,3 次元の色ヒストグラムに対する正規化および閾値処理を行う方法を示します:
void computeNormalizedColorHist(const Mat& image, Mat& hist, int N, double minProb)
{
const int histSize[] = {N, N, N};
// ヒストグラムが適切なサイズと型を確実にもつようにします.
hist.create(3, histSize, CV_32F);
// そして,それをクリアします.
hist = Scalar(0);
// 以下のループは,画像が 8 ビット 3 チャンネルであることを
// 仮定しているので,まずそれをチェックします.
CV_Assert(image.type() == CV_8UC3);
MatConstIterator_<Vec3b> it = image.begin<Vec3b>(),
it_end = image.end<Vec3b>();
for( ; it != it_end; ++it )
{
const Vec3b& pix = *it;
hist.at<float>(pix[0]*N/256, pix[1]*N/256, pix[2]*N/256) += 1.f;
}
minProb *= image.rows*image.cols;
Mat plane;
NAryMatIterator it(&hist, &plane, 1);
double s = 0;
// 行列に対して反復処理を行います.各繰り返しにおいて,
// ( Mat 型の) it.planes[*] は,現在の平面の集合となります.
for(int p = 0; p < it.nplanes; p++, ++it)
{
threshold(it.planes[0], it.planes[0], minProb, 0, THRESH_TOZERO);
s += sum(it.planes[0])[0];
}
s = 1./s;
it = NAryMatIterator(&hist, &plane, 1);
for(int p = 0; p < it.nplanes; p++, ++it)
it.planes[0] *= s;
}
SparseMat¶
n 次元の疎な配列.
class SparseMat
{
public:
typedef SparseMatIterator iterator;
typedef SparseMatConstIterator const_iterator;
// 内部構造体 - 疎な行列のヘッダ
struct Hdr
{
...
};
// 疎な行列のノード - ハッシュテーブルの要素
struct Node
{
size_t hashval;
size_t next;
int idx[CV_MAX_DIM];
};
////////// コンストラクタとデストラクタ //////////
// デフォルトコンストラクタ
SparseMat();
// 指定されたサイズと型の行列を作成します.
SparseMat(int dims, const int* _sizes, int _type);
// コピーコンストラクタ
SparseMat(const SparseMat& m);
// 2 次元の密な配列を,疎な形に変換します.
// try1d が true かつ,行列が 1 列の場合 (Nx1) は,
// 疎な行列も 1 次元になります.
SparseMat(const Mat& m, bool try1d=false);
// 古い形式の疎な行列を,新しい形式に変換します.
// 変換後に "m" を安全に解放できるように,
// すべてのデータがコピーされます.
SparseMat(const CvSparseMat* m);
// デストラクタ
~SparseMat();
///////// 代入演算子 ///////////
// これは O(1) の処理です.データはコピーされません.
SparseMat& operator = (const SparseMat& m);
// ( try1d=false の場合のコンストラクタと等価)
SparseMat& operator = (const Mat& m);
// 行列の完全なコピーを作成します.
SparseMat clone() const;
// 出力行列にすべてのデータをコピーします.
// 必要ならば,出力行列は再割り当てされます.
void copyTo( SparseMat& m ) const;
// 1 次元あるいは 2 次元の疎な行列を, 2 次元の密な行列に変換します.
// 疎な行列が 1 次元である場合,結果として得られる密な行列は,
// 1 列の行列になります.
void copyTo( Mat& m ) const;
// 任意の疎な行列を密な行列に変換します.
// 行列のすべての要素に,指定したスカラを掛けます.
void convertTo( SparseMat& m, int rtype, double alpha=1 ) const;
// 疎な行列を,密な行列に変換します.型の変換やスケーリングなども可能です.
// rtype=-1 の場合,出力される密な行列の要素型は,
// 元の疎な行列の要素型と同じになります.
// それ以外の場合,ビット深度は rtype で指定された値になり,
// チャンネル数は,疎な行列のものと同じになります.
void convertTo( Mat& m, int rtype, double alpha=1, double beta=0 ) const;
// 現在は利用されません.
void assignTo( SparseMat& m, int type=-1 ) const;
// 疎な行列を再割り当てします.既に適切なサイズと型の行列である場合,
// 単に clear() によってデータがクリアされます.そうでない場合,
// 古い行列は( release() によって)解放され,新しい行列が確保されます.
void create(int dims, const int* _sizes, int _type);
// すべての行列要素を 0 にします.これは,ハッシュテーブルのクリアを意味します.
void clear();
// ヘッダの参照カウンタを手動でインクリメントします.
void addref();
// ヘッダの参照カウンタをデクリメントします.カウンタが 0 になると
// ヘッダとすべての内部データが解放されます.
void release();
// 疎な行列を古い形式の表現に変換します.
// すべての要素がコピーされます.
operator CvSparseMat*() const;
// バイト単位で表された各要素サイズ
// (要素のインデックスや SparseMat::Node 要素が存在するので,
// 行列のノードサイズはもっと大きくなります)
size_t elemSize() const;
// elemSize()/channels()
size_t elemSize1() const;
// Mat のものと同じです.
int type() const;
int depth() const;
int channels() const;
// サイズの配列を返し,行列が確保されていない場合は 0 を返します.
const int* size() const;
// i 番目のサイズ(あるいは 0 )を返します.
int size(int i) const;
// 行列の次元数を返します.
int dims() const;
// 0 ではない要素の個数を返します.
size_t nzcount() const;
// 要素のインデックスから,要素のハッシュ値を計算します:
// 1D の場合
size_t hash(int i0) const;
// 2D の場合
size_t hash(int i0, int i1) const;
// 3D の場合
size_t hash(int i0, int i1, int i2) const;
// n-D の場合
size_t hash(const int* idx) const;
// 低レベルな要素アクセス関数:
// 1D, 2D, 3D の場合の特別版と, n-D の場合の汎用版があります.
//
// 行列要素へのポインタを返します.
// 要素が存在する( 0 ではない)場合,そのポインタが返されます.
// 要素が存在せず createMissing=false の場合, NULL ポインタが返されます.
// 要素が存在せず createMissing=true の場合,新しい要素が作成されて
// 0 で初期化されます.そして,そのポインタが返されます.
// hashval ポインタが NULL でない場合,要素のハッシュ値は計算されずに,
// *hashval が代わりに利用されます.
uchar* ptr(int i0, bool createMissing, size_t* hashval=0);
uchar* ptr(int i0, int i1, bool createMissing, size_t* hashval=0);
uchar* ptr(int i0, int i1, int i2, bool createMissing, size_t* hashval=0);
uchar* ptr(const int* idx, bool createMissing, size_t* hashval=0);
// 高レベルな要素アクセス関数:
// ref<_Tp>(i0,...[,hashval]) - *(_Tp*)ptr(i0,...true[,hashval]) と等価です.
// 常に要素への有効な参照を返します.
// 要素が存在しない場合は,新たに作成します.
// find<_Tp>(i0,...[,hashval]) - (_const Tp*)ptr(i0,...false[,hashval]) と等価です.
// 要素が存在すればそのポインタ,存在しなければ NULL を返します.
// value<_Tp>(i0,...[,hashval]) -
// { const _Tp* p = find<_Tp>(i0,...[,hashval]); return p ? *p : _Tp(); } と等価です.
// つまり, 要素が存在しなければ 0 を返します.
// _Tp は,実際の要素型と一致しなければならないことに注意してください -
// この関数は,処理中にいかなる型の変換も行いません.
// 1D の場合
template<typename _Tp> _Tp& ref(int i0, size_t* hashval=0);
template<typename _Tp> _Tp value(int i0, size_t* hashval=0) const;
template<typename _Tp> const _Tp* find(int i0, size_t* hashval=0) const;
// 2D の場合
template<typename _Tp> _Tp& ref(int i0, int i1, size_t* hashval=0);
template<typename _Tp> _Tp value(int i0, int i1, size_t* hashval=0) const;
template<typename _Tp> const _Tp* find(int i0, int i1, size_t* hashval=0) const;
// 3D の場合
template<typename _Tp> _Tp& ref(int i0, int i1, int i2, size_t* hashval=0);
template<typename _Tp> _Tp value(int i0, int i1, int i2, size_t* hashval=0) const;
template<typename _Tp> const _Tp* find(int i0, int i1, int i2, size_t* hashval=0) const;
// n-D の場合
template<typename _Tp> _Tp& ref(const int* idx, size_t* hashval=0);
template<typename _Tp> _Tp value(const int* idx, size_t* hashval=0) const;
template<typename _Tp> const _Tp* find(const int* idx, size_t* hashval=0) const;
// 指定された行列要素を削除します.
// 要素が存在しない場合は何もしません.
void erase(int i0, int i1, size_t* hashval=0);
void erase(int i0, int i1, int i2, size_t* hashval=0);
void erase(const int* idx, size_t* hashval=0);
// 行列のイテレータを返します.
// これは,疎な行列の最初の要素を指すか,
SparseMatIterator begin();
SparseMatConstIterator begin() const;
// ... あるいは,最後の要素の後ろを指します.
SparseMatIterator end();
SparseMatConstIterator end() const;
// 上述のメソッドのテンプレート版.
// _Tp は,実際の行列型と一致しなければいけません.
template<typename _Tp> SparseMatIterator_<_Tp> begin();
template<typename _Tp> SparseMatConstIterator_<_Tp> begin() const;
template<typename _Tp> SparseMatIterator_<_Tp> end();
template<typename _Tp> SparseMatConstIterator_<_Tp> end() const;
// 疎な行列のノードに格納されている値を返します.
template<typename _Tp> _Tp& value(Node* n);
template<typename _Tp> const _Tp& value(const Node* n) const;
////////////// 内部で利用されるメソッド ///////////////
...
// 疎な行列ヘッダへのポインタ
Hdr* hdr;
};
SparseMat クラスは,多次元の疎な数値配列を表します.この疎な配列は, Mat() が格納できるあらゆる型の要素を格納できます.「疎な」というのは,0 ではない要素だけが格納されていることを意味します(しかし,疎な行列を処理した結果,その行列の要素が実際には 0 になる可能性はあります.そのような要素を検出して, SparseMat::erase を用いて削除するかどうかはユーザ次第です).0 ではない要素は,ハッシュテーブルに格納されます.また,(要素が存在する, しないに関係なく)平均探索時間が O(1) となるように,ハッシュテーブルは十分に埋められた時点で拡張されます.要素には以下のメソッドを利用してアクセスできます:
クエリ操作( SparseMat::ptr と,高レベル関数 SparseMat::ref , SparseMat::value , SparseMat::find ),つまり:
const int dims = 5; int size[] = {10, 10, 10, 10, 10}; SparseMat sparse_mat(dims, size, CV_32F); for(int i = 0; i < 1000; i++) { int idx[dims]; for(int k = 0; k < dims; k++) idx[k] = rand() sparse_mat.ref<float>(idx) += 1.f; }
疎な行列のイテレータ. Mat() のイテレータと同様に,疎な行列のイテレータは STL 形式であり,この反復ループは C++ ユーザにとって馴染みあるものでしょう:
// 疎な浮動小数点型行列の要素と, // その要素の合計を表示します. SparseMatConstIterator_<float> it = sparse_mat.begin<float>(), it_end = sparse_mat.end<float>(); double s = 0; int dims = sparse_mat.dims(); for(; it != it_end; ++it) { // 要素のインデックスと要素の値を表示します. const Node* n = it.node(); printf("(") for(int i = 0; i < dims; i++) printf(" printf(": s += *it; } printf("Element sum is
このループを走らせると,要素の表示順がいかなる論理的順序(辞書順,など)にも従わないことに気付くでしょう.これらは,ハッシュテーブルに格納された順番に,つまり,半乱数的に並んでいます.そこで,ノードへのポインタを集めて,適切な順序にソートしようとするかもしれません.しかしそうすると,後から行列に要素を加えたときに,バッファが再割り当てされて,ノードへのポインタが無効になってしまう可能性があることに注意しなければいけません.
2つ以上の疎な行列を同時に処理する必要がある場合の,上述の2つのメソッドの組み合わせ.例えば,次のようにすれば,2つの疎な浮動小数点型行列同士の正規化されていない相関を求めることができます:
double cross_corr(const SparseMat& a, const SparseMat& b) { const SparseMat *_a = &a, *_b = &b; // b の要素数が a よりも少ない場合, // b を反復横断した方が高速です. if(_a->nzcount() > _b->nzcount()) std::swap(_a, _b); SparseMatConstIterator_<float> it = _a->begin<float>(), it_end = _a->end<float>(); double ccorr = 0; for(; it != it_end; ++it) { // 最初の行列から,次の要素を取り出します. float avalue = *it; const Node* anode = it.node(); // 2 番目の行列で同じインデックスをもつ要素を見つけようとします. // ハッシュ値は要素のインデックスにのみ依存するので, // ノードに格納されたハッシュ値を再利用します. float bvalue = _b->value<float>(anode->idx,&anode->hashval); ccorr += avalue*bvalue; } return ccorr; }
SparseMat_¶
SparseMat() から派生した,疎な n 次元配列のクラステンプレート.
template<typename _Tp> class SparseMat_ : public SparseMat
{
public:
typedef SparseMatIterator_<_Tp> iterator;
typedef SparseMatConstIterator_<_Tp> const_iterator;
// コンストラクタ;
// データ型が = DataType<_Tp>::type となる行列を作成します.
SparseMat_();
SparseMat_(int dims, const int* _sizes);
SparseMat_(const SparseMat& m);
SparseMat_(const SparseMat_& m);
SparseMat_(const Mat& m);
SparseMat_(const CvSparseMat* m);
// 代入演算子.必要ならばデータ型を変換します.
SparseMat_& operator = (const SparseMat& m);
SparseMat_& operator = (const SparseMat_& m);
SparseMat_& operator = (const Mat& m);
SparseMat_& operator = (const MatND& m);
// 基底クラスの対応するメソッドと同じです.
SparseMat_ clone() const;
void create(int dims, const int* _sizes);
operator CvSparseMat*() const;
// データ型のチェックを追加するようにオーバーライドされたメソッド.
int type() const;
int depth() const;
int channels() const;
// より便利な要素アクセス演算子.
// ref() はそのまま(ただし, <_Tp> の指定は必要ありません)
// operator () は SparseMat::value<_Tp> と等価です.
_Tp& ref(int i0, size_t* hashval=0);
_Tp operator()(int i0, size_t* hashval=0) const;
_Tp& ref(int i0, int i1, size_t* hashval=0);
_Tp operator()(int i0, int i1, size_t* hashval=0) const;
_Tp& ref(int i0, int i1, int i2, size_t* hashval=0);
_Tp operator()(int i0, int i1, int i2, size_t* hashval=0) const;
_Tp& ref(const int* idx, size_t* hashval=0);
_Tp operator()(const int* idx, size_t* hashval=0) const;
// イテレータ.
SparseMatIterator_<_Tp> begin();
SparseMatConstIterator_<_Tp> begin() const;
SparseMatIterator_<_Tp> end();
SparseMatConstIterator_<_Tp> end() const;
};
SparseMat_ は, Mat_ と同じように作成された, SparseMat() に被せる薄いラッパーです. これによって,いくつかの処理が次のように簡単に書けるようになります.
int sz[] = {10, 20, 30};
SparseMat_<double> M(3, sz);
...
M.ref(1, 2, 3) = M(4, 5, 6) + M(7, 8, 9);
ヘルプとフィードバック
お探しの情報が見つかりませんか?- チーシート(PDF) を読んでみてください.
- ユーザグループ/メーリングリスト (英語)で質問してみてください.
- このドキュメントに誤りなどを見つけたらbug report まで報告してください.また,日本語訳に関する誤りや指摘はOpenCV.jpまでお願いします.
