ヒストグラム¶
cv::calcHist¶
- void calcHist(const Mat* arrays, int narrays, const int* channels, const Mat& mask, MatND& hist, int dims, const int* histSize, const float** ranges, bool uniform=true, bool accumulate=false)¶
- void calcHist(const Mat* arrays, int narrays, const int* channels, const Mat& mask, SparseMat& hist, int dims, const int* histSize, const float** ranges, bool uniform=true, bool accumulate=false)
配列の集合のヒストグラムを求めます.
パラメタ: - arrays – 入力配列.各配列はすべて同じビット深度 CV_8U または CV_32F で,同じサイズですが,それぞれは任意のチャンネル数を持てます.
- narrays – 入力配列の個数.
- channels – 各次元のヒストグラムを求めるために利用するチャンネルを示す,サイズ dims のリストです.1番目の配列のチャンネルは,0 から arrays[0].channels()-1 までで表現されます.同様に,2番目の配列 のチャンネルは, arrays[0].channels() から arrays[0].channels() + arrays[1].channels()-1 までで表現されます.
- mask – オプションマスク.この行列が空ではない場合, arrays[i] と同じサイズで8ビットの配列でなければいけません.0以外の要素は,ヒストグラムでカウントされる配列要素を表します.
- hist – 出力されるヒストグラム.密あるいは疎な dims -次元の配列.
- dims – ヒストグラムの次元数.正値であり,かつ CV_MAX_DIMS (現バージョンのOpenCVでは =32)以下の値でなければいけません.
- histSize – 各次元のヒストグラムサイズの配列.
- ranges – 各次元におけるヒストグラムのビンの境界を表す dims 個の配列,の配列.ヒストグラムが一様な場合( uniform =true )は, i 次元の,0番目のヒストグラムビンの下限(範囲に含む)
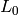 と,最後のヒストグラムビン histSize[i]-1 の上限(範囲に含まない)
と,最後のヒストグラムビン histSize[i]-1 の上限(範囲に含まない) ![U_{\texttt{histSize}[i]-1}](_images/math/b6b12dbd611a0d5e704d20a16dc23bf5a5d9c471.png) を指定すれば十分です.つまり,一様なヒストグラムの場合,各 ranges[i] が2要素の配列となります.ヒストグラムが一様ではない場合( uniform=false )は,各 i において, histSize[i]+1 個の要素を含みます:
を指定すれば十分です.つまり,一様なヒストグラムの場合,各 ranges[i] が2要素の配列となります.ヒストグラムが一様ではない場合( uniform=false )は,各 i において, histSize[i]+1 個の要素を含みます: ![L_0, U_0=L_1, U_1=L_2, ..., U_{\texttt{histSize[i]}-2}=L_{\texttt{histSize[i]}-1}, U_{\texttt{histSize[i]}-1}](_images/math/2b32e933a4da6b24d4c0e39c8857367ef58224e4.png) また,
また, 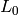 と
と ![U_{\texttt{histSize[i]}-1}](_images/math/971ddbd37692eb5abdcc491285cff96ace563bd2.png) の間に存在しない配列の要素は,ヒストグラムではカウントされません.
の間に存在しない配列の要素は,ヒストグラムではカウントされません. - uniform – ヒストグラムが一様か,そうでないかを示します.上記の説明を参照してください.
- accumulate – 累積フラグ.これが設定されると,(ヒストグラムが確保されている場合)最初にヒストグラムのクリアが行われません.これによって,複数の配列集合に対する1つのヒストグラムを計算したり,毎回ヒストグラムを更新したりすることができます.
関数 calcHist は,1つあるいは複数の配列に対するヒストグラムを求めます. ヒストグラムのビンの値を増加させるタプル要素は,対応する(複数の)入力配列の同じ位置から取り出されます. 次のサンプルは,カラー画像の色相-彩度の2次元ヒストグラムを求める例です.
#include <cv.h>
#include <highgui.h>
using namespace cv;
int main( int argc, char** argv )
{
Mat src, hsv;
if( argc != 2 || !(src=imread(argv[1], 1)).data )
return -1;
cvtColor(src, hsv, CV_BGR2HSV);
// 色相を 30 分割レベルで,
// 彩度を 32 分割レベルで量子化します
int hbins = 30, sbins = 32;
int histSize[] = {hbins, sbins};
// cvtColor にあるように,色相の範囲は 0 から 179 です.
float hranges[] = { 0, 180 };
// 彩度の範囲は 0 (黒-灰色-白)から
// 255 (純粋なスペクトルカラー)までです.
float sranges[] = { 0, 256 };
const float* ranges[] = { hranges, sranges };
MatND hist;
// 0 番目と 1 番目のチャンネルからヒストグラムを求めます.
int channels[] = {0, 1};
calcHist( &hsv, 1, channels, Mat(), // マスクは利用しません
hist, 2, histSize, ranges,
true, // ヒストグラムは一様です
false );
double maxVal=0;
minMaxLoc(hist, 0, &maxVal, 0, 0);
int scale = 10;
Mat histImg = Mat::zeros(sbins*scale, hbins*10, CV_8UC3);
for( int h = 0; h < hbins; h++ )
for( int s = 0; s < sbins; s++ )
{
float binVal = hist.at<float>(h, s);
int intensity = cvRound(binVal*255/maxVal);
rectangle( histImg, Point(h*scale, s*scale),
Point( (h+1)*scale - 1, (s+1)*scale - 1),
Scalar::all(intensity),
CV_FILLED );
}
namedWindow( "Source", 1 );
imshow( "Source", src );
namedWindow( "H-S Histogram", 1 );
imshow( "H-S Histogram", histImg );
waitKey();
}
cv::calcBackProject¶
- void calcBackProject(const Mat* arrays, int narrays, const int* channels, const MatND& hist, Mat& backProject, const float** ranges, double scale=1, bool uniform=true)¶
- void calcBackProject(const Mat* arrays, int narrays, const int* channels, const SparseMat& hist, Mat& backProject, const float** ranges, double scale=1, bool uniform=true)
ヒストグラムのバックプロジェクションを求めます.
パラメタ: - arrays – 入力配列.各配列はすべて同じビット深度 CV_8U または CV_32F ,同じサイズですが,それぞれは任意のチャンネル数をもてます.
- narrays – 入力配列の個数.
- channels – 各次元のヒストグラムを求めるために利用するチャンネルを示す,サイズ dims のリスト.1番目の配列のチャンネルは,0 から arrays[0].channels()-1 までで表現されます.同様に,2番目の配列のチャンネルは, arrays[0].channels() から arrays[0].channels() + arrays[1].channels()-1 までで表現されます.
- hist – 入力ヒストグラム.密あるいは疎な dims -次元の配列.
- backProject – 出力されるバックプロジェクション配列. arrays[0] と同じサイズ,同じビット深度のシングルチャンネル配列.
- ranges – 各次元におけるヒストグラムビンの境界を表す配列の配列. calcHist を参照してください.
- scale – オプション.出力されるバックプロジェクションのスケールファクタ.
- uniform – ヒストグラムが一様か,そうでないかを示します.
関数 calcBackProject は,ヒストグラムのバックプロジェクションを求めます.つまり calcHist と同様に,入力画像の指定チャンネルの座標 (x, y) における値を取得し,それに対応するヒストグラムのビンを求めます.この関数では,そのビンの値を増加させるのではなく値を読み出し,それを scale でスケーリングして, backProject(x, y) に格納します.統計学の用語で言えば,これは,ヒストグラムで表現された経験的確率分布における,各要素値の確率を求める関数です.ここでは例として,シーン中の明るい色の物体を検出し追跡する方法を示します:
- 追跡の前に,追跡したい物体をカメラの画面いっぱいに写します.そして,その色相のヒストグラムを求めます.ヒストグラムはおそらく,物体の主な色に対応する箇所で強いピークをもつでしょう.
- 物体の追跡中,(上記のようにして)事前に求めたヒストグラムを利用して,入力ビデオ画像の色相平面のバックプロジェクションを計算します.またここで,適切な彩度ではないピクセルや,暗すぎたり明るすぎたりするピクセルを除外するのも良いでしょう.
- 結果画像から連結成分を検出し,例えば最も大きな成分を選択します.
つまり,これは CAMShift カラー物体追跡器の近似アルゴリズムです.
参考: calcHist()
cv::compareHist¶
- double compareHist(const MatND& H1, const MatND& H2, int method)¶
- double compareHist(const SparseMat& H1, const SparseMat& H2, int method)
2つのヒストグラムを比較します.
パラメタ: - H1 – 比較される 1 番目のヒストグラム.
- H2 – 比較される 2 番目のヒストグラム. H1 と同じサイズです.
- method –
比較手法.次のうちの1つ:
- CV_COMP_CORREL 相関
- CV_COMP_CHISQR カイ2乗
- CV_COMP_INTERSECT 交差
- CV_COMP_BHATTACHARYYA Bhattacharyya距離
関数 compareHist は,指定の手法を用いて,2つの密または疎なヒストグラム同士を比較します.
相関 (method=CV_COMP_CORREL)
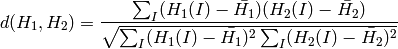
ここで
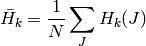
です.また
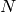 は,ヒストグラムのビンの総数を表します.
は,ヒストグラムのビンの総数を表します.カイ2乗 (method=CV_COMP_CHISQR)
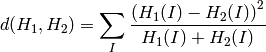
交差 (method=CV_COMP_INTERSECT)
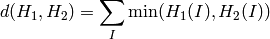
Bhattacharyya 距離 (method=CV_COMP_BHATTACHARYYA)
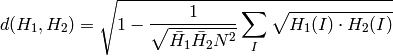
この関数は,
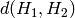 を返します.
を返します.
この関数は,1-, 2-, 3-次元の密なヒストグラムに対しては上手く動作しますが,高次元の疎なヒストグラムに対しては適切なものではありません.なぜなら,エイリアシングやサンプリングの問題により,0ではないヒストグラムビンの座標が僅かにずれるからです.このようなヒストグラムや,より一般的な疎構造である重み付き点群同士を比較する場合には,関数 calcEMD の利用を検討してください.
cv::equalizeHist¶
- void equalizeHist(const Mat& src, Mat& dst)¶
グレースケール画像のヒストグラムを均一化します.
パラメタ: - src – 8ビット,シングルチャンネルの入力画像.
- dst – src と同じサイズ,同じタイプの出力画像.
関数 equalizeHist は,以下のアルゴリズムを用いて入力画像のヒストグラムを均一化します.
src のヒストグラム
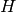 を求めます.
を求めます.ヒストグラムビンの合計値が 255 になるように,ヒストグラムを正規化します.
ヒストグラムの積分値を次のように求めます:
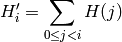
 をルックアップテーブルとして利用して,画像を変換します:
をルックアップテーブルとして利用して,画像を変換します:
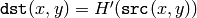
このアルゴリズムは,画像の明るさを正規化し,コントラストを上げます.
ヘルプとフィードバック
お探しの情報が見つかりませんか?- チーシート(PDF) を読んでみてください.
- ユーザグループ/メーリングリスト (英語)で質問してみてください.
- このドキュメントに誤りなどを見つけたらbug report まで報告してください.また,日本語訳に関する誤りや指摘はOpenCV.jpまでお願いします.
