EMアルゴリズム¶
EM (Expectation-Maximization) アルゴリズムは,混合数が既知である混合ガウス分布の多変量確率密度関数のパラメータを推定します.
特徴ベクトルの集合
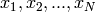 を考えます:ここで,d-次元ユークリッド空間の N 個のベクトルは,混合ガウス分布に従って選択されます:
を考えます:ここで,d-次元ユークリッド空間の N 個のベクトルは,混合ガウス分布に従って選択されます:
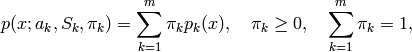
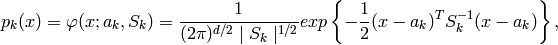
ここで,
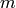 は混合数,
は混合数,
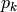 は平均が
は平均が
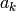 で共分散行列が
で共分散行列が
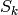 である正規分布の確率密度,
である正規分布の確率密度,
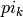 はk番目の分布に対する重み,を表します.混合数
はk番目の分布に対する重み,を表します.混合数
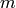 とサンプル
とサンプル
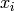 ,
,
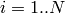 が与えられると,このアルゴリズムは,すべての混合分布パラメータ,つまり
が与えられると,このアルゴリズムは,すべての混合分布パラメータ,つまり
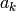 ,
,
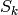 ,
,
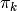 に対する最尤推定(MLE)を行います.
に対する最尤推定(MLE)を行います.
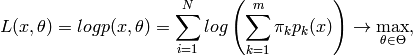
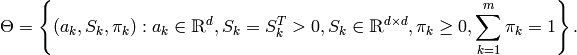
EMアルゴリズムでは,反復計算が行われます.それぞれの試行は,2つのステップから構成されます.1番目のステップ(Expectation-ステップ,または E-ステップ)では,混合分布パラメータのその時点の推定値を用いて,サンプル
i
が分布
k
に属する確率
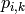 (以下の式では
(以下の式では
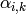 で表されます) を求めます:
で表されます) を求めます:
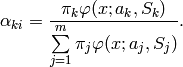
2番目のステップ(Maximization-ステップ, またはM-ステップ)では,求められた確率を用いて,混合分布パラメータの推定値を最大化します:
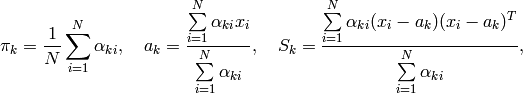
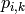 の初期値が与えられている場合には,このアルゴリズムを M-ステップから開始する方法もあります.また,
の初期値が与えられている場合には,このアルゴリズムを M-ステップから開始する方法もあります.また,
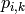 が未知の場合,入力サンプルをあらかじめクラスタリングして
が未知の場合,入力サンプルをあらかじめクラスタリングして
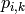 の初期値を得るために,より単純なクラスタリングアルゴリズムを用いるという方法もあります.このような場合
KMeans2
アルゴリズムがよく用いられます(ML の場合も,そうなっています).
の初期値を得るために,より単純なクラスタリングアルゴリズムを用いるという方法もあります.このような場合
KMeans2
アルゴリズムがよく用いられます(ML の場合も,そうなっています).
EMアルゴリズムが対処すべき問題の1つが,膨大な推定パラメータの数です.このパラメータの大部分は共分散行列で表現されており,それぞれの行列が
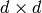 の要素を持ちます(ここで
の要素を持ちます(ここで
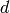 は特徴空間の次元です).しかし,実際の問題では多くの場合,この共分散行列は対角行列,あるいは
は特徴空間の次元です).しかし,実際の問題では多くの場合,この共分散行列は対角行列,あるいは
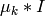 (ここで
(ここで
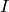 は単位行列,
は単位行列,
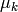 は混合分布に依存する「スケール」パラメータ)に近い形をしています.したがって,ロバストな計算を行うために,共分散行列に強い制約条件を設けた状態で計算を開始し,そこで推定されたパラメータを入力として,弱い制約条件下での最適化問題を解くという方法が考えられます(対角共分散行列は,既に十分な精度の近似値になっていることも多々あります).
は混合分布に依存する「スケール」パラメータ)に近い形をしています.したがって,ロバストな計算を行うために,共分散行列に強い制約条件を設けた状態で計算を開始し,そこで推定されたパラメータを入力として,弱い制約条件下での最適化問題を解くという方法が考えられます(対角共分散行列は,既に十分な精度の近似値になっていることも多々あります).
参考文献:
- Bilmes98 J. A. Bilmes. A Gentle Tutorial of the EM Algorithm and its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models. Technical Report TR-97-021, International Computer Science Institute and Computer Science Division, University of California at Berkeley, April 1998.
CvEMParams¶
- CvEMParams¶
EMアルゴリズムのパラメータ.
struct CvEMParams
{
CvEMParams() : nclusters(10), cov_mat_type(CvEM::COV_MAT_DIAGONAL),
start_step(CvEM::START_AUTO_STEP), probs(0), weights(0), means(0),
covs(0)
{
term_crit=cvTermCriteria( CV_TERMCRIT_ITER+CV_TERMCRIT_EPS,
100, FLT_EPSILON );
}
CvEMParams( int _nclusters, int _cov_mat_type=1/*CvEM::COV_MAT_DIAGONAL*/,
int _start_step=0/*CvEM::START_AUTO_STEP*/,
CvTermCriteria _term_crit=cvTermCriteria(
CV_TERMCRIT_ITER+CV_TERMCRIT_EPS,
100, FLT_EPSILON),
CvMat* _probs=0, CvMat* _weights=0,
CvMat* _means=0, CvMat** _covs=0 ) :
nclusters(_nclusters), cov_mat_type(_cov_mat_type),
start_step(_start_step),
probs(_probs), weights(_weights), means(_means), covs(_covs),
term_crit(_term_crit)
{}
int nclusters;
int cov_mat_type;
int start_step;
const CvMat* probs;
const CvMat* weights;
const CvMat* means;
const CvMat** covs;
CvTermCriteria term_crit;
};
この構造体には,2つのコンストラクタがあります.デフォルトコンストラクタは,大まかな経験則に則ったもので,もう1つのコンストラクタは,(唯一不可欠な,問題依存のパラメータである)混合数から,混合パラメータの初期値まで,様々なパラメータを変更できるものです.
CvEM¶
- CvEM¶
EMモデル.
class CV_EXPORTS CvEM : public CvStatModel
{
public:
// 共分散行列の種類
enum { COV_MAT_SPHERICAL=0, COV_MAT_DIAGONAL=1, COV_MAT_GENERIC=2 };
// 開始ステップ
enum { START_E_STEP=1, START_M_STEP=2, START_AUTO_STEP=0 };
CvEM();
CvEM( const CvMat* samples, const CvMat* sample_idx=0,
CvEMParams params=CvEMParams(), CvMat* labels=0 );
virtual ~CvEM();
virtual bool train( const CvMat* samples, const CvMat* sample_idx=0,
CvEMParams params=CvEMParams(), CvMat* labels=0 );
virtual float predict( const CvMat* sample, CvMat* probs ) const;
virtual void clear();
int get_nclusters() const { return params.nclusters; }
const CvMat* get_means() const { return means; }
const CvMat** get_covs() const { return covs; }
const CvMat* get_weights() const { return weights; }
const CvMat* get_probs() const { return probs; }
protected:
virtual void set_params( const CvEMParams& params,
const CvVectors& train_data );
virtual void init_em( const CvVectors& train_data );
virtual double run_em( const CvVectors& train_data );
virtual void init_auto( const CvVectors& samples );
virtual void kmeans( const CvVectors& train_data, int nclusters,
CvMat* labels, CvTermCriteria criteria,
const CvMat* means );
CvEMParams params;
double log_likelihood;
CvMat* means;
CvMat** covs;
CvMat* weights;
CvMat* probs;
CvMat* log_weight_div_det;
CvMat* inv_eigen_values;
CvMat** cov_rotate_mats;
};
CvEM::train¶
- void CvEM::train(const CvMat* samples, const CvMat* sample_idx=0, CvEMParams params=CvEMParams(), CvMat* labels=0)¶
サンプル集合から,混合ガウス分布のパラメータを推定します.
多くのMLモデルとは異なり,EMは教師なし学習アルゴリズムなので,学習時に入力に対する応答(クラスラベルや関数値)を必要としません.その代わりに,入力サンプル集合から混合ガウス分布パラメータの
MLE
(最尤推定値)を求め,すべてのパラメータを次のように構造体に格納します:
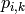 を
probs
に,
を
probs
に,
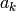 を
means
に,
を
means
に,
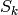 を
covs[k]
に,
を
covs[k]
に,
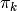 を
weights
に.そして,オプションとして,それぞれのサンプルに対する出力「クラスラベル」を次のように計算します:
を
weights
に.そして,オプションとして,それぞれのサンプルに対する出力「クラスラベル」を次のように計算します:
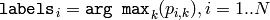 (つまり,各サンプルが属する最も確からしい分布のインデックス).
(つまり,各サンプルが属する最も確からしい分布のインデックス).
他の分類器と同様に,学習されたモデルを用いて予測を行うことができます.このモデルは, Bayes classifier と似ています.
例:複数のガウス分布からランダムにサンプリングされたデータを,EMを用いてクラスタリングします.
#include "ml.h"
#include "highgui.h"
int main( int argc, char** argv )
{
const int N = 4;
const int N1 = (int)sqrt((double)N);
const CvScalar colors[] = {{0,0,255}},{{0,255,0}},
{{0,255,255}},{{255,255,0}
;
int i, j;
int nsamples = 100;
CvRNG rng_state = cvRNG(-1);
CvMat* samples = cvCreateMat( nsamples, 2, CV_32FC1 );
CvMat* labels = cvCreateMat( nsamples, 1, CV_32SC1 );
IplImage* img = cvCreateImage( cvSize( 500, 500 ), 8, 3 );
float _sample[2];
CvMat sample = cvMat( 1, 2, CV_32FC1, _sample );
CvEM em_model;
CvEMParams params;
CvMat samples_part;
cvReshape( samples, samples, 2, 0 );
for( i = 0; i < N; i++ )
{
CvScalar mean, sigma;
// 学習サンプルから
cvGetRows( samples, &samples_part, i*nsamples/N,
(i+1)*nsamples/N );
mean = cvScalar(((i
((i/N1)+1.)*img->height/(N1+1));
sigma = cvScalar(30,30);
cvRandArr( &rng_state, &samples_part, CV_RAND_NORMAL,
mean, sigma );
}
cvReshape( samples, samples, 1, 0 );
// モデルのパラメータを初期化します
params.covs = NULL;
params.means = NULL;
params.weights = NULL;
params.probs = NULL;
params.nclusters = N;
params.cov_mat_type = CvEM::COV_MAT_SPHERICAL;
params.start_step = CvEM::START_AUTO_STEP;
params.term_crit.max_iter = 10;
params.term_crit.epsilon = 0.1;
params.term_crit.type = CV_TERMCRIT_ITER|CV_TERMCRIT_EPS;
// データをクラスタリングします
em_model.train( samples, 0, params, labels );
#if 0
// 1番目のステージの出力を2番目のステージの入力として使う時に,
// 弱い拘束のパラメータ( COV_MAT_SPHERICAL の代わりに COV_MAT_DIAGONAL )
// を用いてモデルの繰り返し最適化を行う簡単な例
CvEM em_model2;
params.cov_mat_type = CvEM::COV_MAT_DIAGONAL;
params.start_step = CvEM::START_E_STEP;
params.means = em_model.get_means();
params.covs = (const CvMat**)em_model.get_covs();
params.weights = em_model.get_weights();
em_model2.train( samples, 0, params, labels );
// em_model2 を利用するためには,以下の em_model.predict()
// を em_model2.predict() に置き換えてください.
#endif
// すべての画像ピクセルを分類します.
cvZero( img );
for( i = 0; i < img->height; i++ )
{
for( j = 0; j < img->width; j++ )
{
CvPoint pt = cvPoint(j, i);
sample.data.fl[0] = (float)j;
sample.data.fl[1] = (float)i;
int response = cvRound(em_model.predict( &sample, NULL ));
CvScalar c = colors[response];
cvCircle( img, pt, 1, cvScalar(c.val[0]*0.75,
c.val[1]*0.75,c.val[2]*0.75), CV_FILLED );
}
}
// クラスタリングされたサンプルを描画します.
for( i = 0; i < nsamples; i++ )
{
CvPoint pt;
pt.x = cvRound(samples->data.fl[i*2]);
pt.y = cvRound(samples->data.fl[i*2+1]);
cvCircle( img, pt, 1, colors[labels->data.i[i]], CV_FILLED );
}
cvNamedWindow( "EM-clustering result", 1 );
cvShowImage( "EM-clustering result", img );
cvWaitKey(0);
cvReleaseMat( &samples );
cvReleaseMat( &labels );
return 0;
}
ヘルプとフィードバック
お探しの情報が見つかりませんか?- チーシート(PDF) を読んでみてください.
- ユーザグループ/メーリングリスト (英語)で質問してみてください.
- このドキュメントに誤りなどを見つけたらbug report まで報告してください.また,日本語訳に関する誤りや指摘はOpenCV.jpまでお願いします.
