Navigation

Structural Analysis and Shape Descriptors

cv::moments

Comments from the Wiki

Moments moments(const Mat& array, bool binaryImage=false)

Calculates all of the moments up to the third order of a polygon or rasterized shape.

where the class Moments is defined as:

class Moments
{
public:
    Moments();
    Moments(double m00, double m10, double m01, double m20, double m11,
            double m02, double m30, double m21, double m12, double m03 );
    Moments( const CvMoments& moments );
    operator CvMoments() const;

    // spatial moments
    double  m00, m10, m01, m20, m11, m02, m30, m21, m12, m03;
    // central moments
    double  mu20, mu11, mu02, mu30, mu21, mu12, mu03;
    // central normalized moments
    double  nu20, nu11, nu02, nu30, nu21, nu12, nu03;
};
param array:A raster image (single-channel, 8-bit or floating-point 2D array) or an array ( 1 \times N or N \times 1 ) of 2D points ( Point or Point2f )
param binaryImage:
 (For images only) If it is true, then all the non-zero image pixels are treated as 1’s

The function computes moments, up to the 3rd order, of a vector shape or a rasterized shape. In case of a raster image, the spatial moments 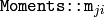\texttt{Moments::m}_{ji} are computed as:

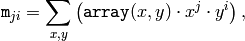
\texttt{m} _{ji}= \sum _{x,y} \left ( \texttt{array} (x,y) \cdot x^j \cdot y^i \right ),

the central moments 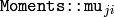\texttt{Moments::mu}_{ji} are computed as:

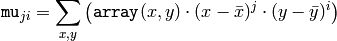
\texttt{mu} _{ji}= \sum _{x,y} \left ( \texttt{array} (x,y) \cdot (x - \bar{x} )^j \cdot (y - \bar{y} )^i \right )

where 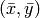(\bar{x}, \bar{y}) is the mass center:

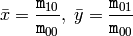
\bar{x} = \frac{\texttt{m}_{10}}{\texttt{m}_{00}} , \; \bar{y} = \frac{\texttt{m}_{01}}{\texttt{m}_{00}}

and the normalized central moments 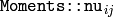\texttt{Moments::nu}_{ij} are computed as:

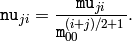
\texttt{nu} _{ji}= \frac{\texttt{mu}_{ji}}{\texttt{m}_{00}^{(i+j)/2+1}} .

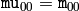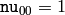
Note that 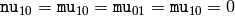\texttt{mu}_{00}=\texttt{m}_{00} , \texttt{nu}_{00}=1 \texttt{nu}_{10}=\texttt{mu}_{10}=\texttt{mu}_{01}=\texttt{mu}_{10}=0 , hence the values are not stored.

The moments of a contour are defined in the same way, but computed using Green’s formula (see http://en.wikipedia.org/wiki/Green_theorem ), therefore, because of a limited raster resolution, the moments computed for a contour will be slightly different from the moments computed for the same contour rasterized.

See also: contourArea() , arcLength()

cv::HuMoments

Comments from the Wiki

void HuMoments(const Moments& moments, double h[7])

Calculates the seven Hu invariants.

Parameters:
  • moments – The input moments, computed with moments()
  • h – The output Hu invariants

The function calculates the seven Hu invariants, see http://en.wikipedia.org/wiki/Image_moment , that are defined as:

\begin{array}{l} h[0]= \eta _{20}+ \eta _{02} \\ h[1]=( \eta _{20}- \eta _{02})^{2}+4 \eta _{11}^{2} \\ h[2]=( \eta _{30}-3 \eta _{12})^{2}+ (3 \eta _{21}- \eta _{03})^{2} \\ h[3]=( \eta _{30}+ \eta _{12})^{2}+ ( \eta _{21}+ \eta _{03})^{2} \\ h[4]=( \eta _{30}-3 \eta _{12})( \eta _{30}+ \eta _{12})[( \eta _{30}+ \eta _{12})^{2}-3( \eta _{21}+ \eta _{03})^{2}]+(3 \eta _{21}- \eta _{03})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}] \\ h[5]=( \eta _{20}- \eta _{02})[( \eta _{30}+ \eta _{12})^{2}- ( \eta _{21}+ \eta _{03})^{2}]+4 \eta _{11}( \eta _{30}+ \eta _{12})( \eta _{21}+ \eta _{03}) \\ h[6]=(3 \eta _{21}- \eta _{03})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}]-( \eta _{30}-3 \eta _{12})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}] \\ \end{array}

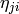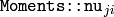where \eta_{ji} stand for \texttt{Moments::nu}_{ji} .

These values are proved to be invariant to the image scale, rotation, and reflection except the seventh one, whose sign is changed by reflection. Of course, this invariance was proved with the assumption of infinite image resolution. In case of a raster images the computed Hu invariants for the original and transformed images will be a bit different.

See also: matchShapes()

cv::findContours

Comments from the Wiki

void findContours(const Mat& image, vector<vector<Point> >& contours, vector<Vec4i>& hierarchy, int mode, int method, Point offset=Point())
void findContours(const Mat& image, vector<vector<Point> >& contours, int mode, int method, Point offset=Point())

Finds the contours in a binary image.

Parameters:
  • image – The source, an 8-bit single-channel image. Non-zero pixels are treated as 1’s, zero pixels remain 0’s - the image is treated as binary . You can use compare() , inRange() , threshold() , adaptiveThreshold() , Canny() etc. to create a binary image out of a grayscale or color one. The function modifies the image while extracting the contours
  • contours – The detected contours. Each contour is stored as a vector of points
  • hiararchy – The optional output vector that will contain information about the image topology. It will have as many elements as the number of contours. For each contour contours[i] , the elements hierarchy[i][0] , hiearchy[i][1] , hiearchy[i][2] , hiearchy[i][3] will be set to 0-based indices in contours of the next and previous contours at the same hierarchical level, the first child contour and the parent contour, respectively. If for some contour i there is no next, previous, parent or nested contours, the corresponding elements of hierarchy[i] will be negative
  • mode –

    The contour retrieval mode

    • CV_RETR_EXTERNAL retrieves only the extreme outer contours; It will set hierarchy[i][2]=hierarchy[i][3]=-1 for all the contours
    • CV_RETR_LIST retrieves all of the contours without establishing any hierarchical relationships
    • CV_RETR_CCOMP retrieves all of the contours and organizes them into a two-level hierarchy: on the top level are the external boundaries of the components, on the second level are the boundaries of the holes. If inside a hole of a connected component there is another contour, it will still be put on the top level
    • CV_RETR_TREE retrieves all of the contours and reconstructs the full hierarchy of nested contours. This full hierarchy is built and shown in OpenCV contours.c demo
  • method –

    The contour approximation method.

    • CV_CHAIN_APPROX_NONE stores absolutely all the contour points. That is, every 2 points of a contour stored with this method are 8-connected neighbors of each other
    • CV_CHAIN_APPROX_SIMPLE compresses horizontal, vertical, and diagonal segments and leaves only their end points. E.g. an up-right rectangular contour will be encoded with 4 points
    • CV_CHAIN_APPROX_TC89_L1,CV_CHAIN_APPROX_TC89_KCOS applies one of the flavors of the Teh-Chin chain approximation algorithm; see TehChin89
  • offset – The optional offset, by which every contour point is shifted. This is useful if the contours are extracted from the image ROI and then they should be analyzed in the whole image context

The function retrieves contours from the binary image using the algorithm Suzuki85 . The contours are a useful tool for shape analysis and object detection and recognition. See squares.c in the OpenCV sample directory.

Note: the source image is modified by this function.

cv::drawContours

Comments from the Wiki

void drawContours(Mat& image, const vector<vector<Point> >& contours, int contourIdx, const Scalar& color, int thickness=1, int lineType=8, const vector<Vec4i>& hierarchy=vector<Vec4i>(), int maxLevel=INT_MAX, Point offset=Point())

Draws contours’ outlines or filled contours.

Parameters:
  • image – The destination image
  • contours – All the input contours. Each contour is stored as a point vector
  • contourIdx – Indicates the contour to draw. If it is negative, all the contours are drawn
  • color – The contours’ color
  • thickness – Thickness of lines the contours are drawn with. If it is negative (e.g. thickness=CV_FILLED ), the contour interiors are drawn.
  • lineType – The line connectivity; see line() description
  • hierarchy – The optional information about hierarchy. It is only needed if you want to draw only some of the contours (see maxLevel )
  • maxLevel – Maximal level for drawn contours. If 0, only the specified contour is drawn. If 1, the function draws the contour(s) and all the nested contours. If 2, the function draws the contours, all the nested contours and all the nested into nested contours etc. This parameter is only taken into account when there is hierarchy available.
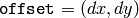
  • offset – The optional contour shift parameter. Shift all the drawn contours by the specified \texttt{offset}=(dx,dy)

The function draws contour outlines in the image if 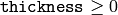\texttt{thickness} \ge 0 or fills the area bounded by the contours if 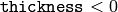\texttt{thickness}<0 . Here is the example on how to retrieve connected components from the binary image and label them

#include "cv.h"
#include "highgui.h"

using namespace cv;

int main( int argc, char** argv )
{
    Mat src;
    // the first command line parameter must be file name of binary
    // (black-n-white) image
    if( argc != 2 || !(src=imread(argv[1], 0)).data)
        return -1;

    Mat dst = Mat::zeros(src.rows, src.cols, CV_8UC3);

    src = src > 1;
    namedWindow( "Source", 1 );
    imshow( "Source", src );

    vector<vector<Point> > contours;
    vector<Vec4i> hierarchy;

    findContours( src, contours, hierarchy,
        CV_RETR_CCOMP, CV_CHAIN_APPROX_SIMPLE );

    // iterate through all the top-level contours,
    // draw each connected component with its own random color
    int idx = 0;
    for( ; idx >= 0; idx = hierarchy[idx][0] )
    {
        Scalar color( rand()&255, rand()&255, rand()&255 );
        drawContours( dst, contours, idx, color, CV_FILLED, 8, hierarchy );
    }

    namedWindow( "Components", 1 );
    imshow( "Components", dst );
    waitKey(0);
}

cv::approxPolyDP

Comments from the Wiki

void approxPolyDP(const Mat& curve, vector<Point>& approxCurve, double epsilon, bool closed)
void approxPolyDP(const Mat& curve, vector<Point2f>& approxCurve, double epsilon, bool closed)

Approximates polygonal curve(s) with the specified precision.

Parameters:
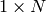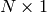  • curve – The polygon or curve to approximate. Must be 1 \times N or N \times 1 matrix of type CV_32SC2 or CV_32FC2 . You can also convert vector<Point> or vector<Point2f to the matrix by calling Mat(const vector<T>&) constructor.
  • approxCurve – The result of the approximation; The type should match the type of the input curve
  • epsilon – Specifies the approximation accuracy. This is the maximum distance between the original curve and its approximation
  • closed – If true, the approximated curve is closed (i.e. its first and last vertices are connected), otherwise it’s not

The functions approxPolyDP approximate a curve or a polygon with another curve/polygon with less vertices, so that the distance between them is less or equal to the specified precision. It used Douglas-Peucker algorithm http://en.wikipedia.org/wiki/Ramer-Douglas-Peucker_algorithm

cv::arcLength

Comments from the Wiki

double arcLength(const Mat& curve, bool closed)

Calculates a contour perimeter or a curve length.

Parameters:
  • curve – The input vector of 2D points, represented by CV_32SC2 or CV_32FC2 matrix, or by vector<Point> or vector<Point2f> converted to a matrix with Mat(const vector<T>&) constructor
  • closed – Indicates, whether the curve is closed or not

The function computes the curve length or the closed contour perimeter.

cv::boundingRect

Comments from the Wiki

Rect boundingRect(const Mat& points)

Calculates the up-right bounding rectangle of a point set.

Parameters:
  • points – The input 2D point set, represented by CV_32SC2 or CV_32FC2 matrix, or by vector<Point> or vector<Point2f> converted to the matrix using Mat(const vector<T>&) constructor.

The function calculates and returns the minimal up-right bounding rectangle for the specified point set.

cv::estimateRigidTransform

Comments from the Wiki

Mat estimateRigidTransform(const Mat& srcpt, const Mat& dstpt, bool fullAffine)

Computes optimal affine transformation between two 2D point sets

Parameters:
  • srcpt – The first input 2D point set
  • dst – The second input 2D point set of the same size and the same type as A
  • fullAffine – If true, the function finds the optimal affine transformation with no any additional resrictions (i.e. there are 6 degrees of freedom); otherwise, the class of transformations to choose from is limited to combinations of translation, rotation and uniform scaling (i.e. there are 5 degrees of freedom)

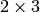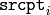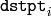The function finds the optimal affine transform [A|b] (a 2 \times 3 floating-point matrix) that approximates best the transformation from \texttt{srcpt}_i to \texttt{dstpt}_i :

[A^*|b^*] = arg \min _{[A|b]} \sum _i \| \texttt{dstpt} _i - A { \texttt{srcpt} _i}^T - b \| ^2

where [A|b] can be either arbitrary (when fullAffine=true ) or have form

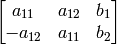
\begin{bmatrix} a_{11} & a_{12} & b_1 \\ -a_{12} & a_{11} & b_2 \end{bmatrix}

when fullAffine=false .

See also: getAffineTransform() , getPerspectiveTransform() , findHomography()

cv::estimateAffine3D

Comments from the Wiki

int estimateAffine3D(const Mat& srcpt, const Mat& dstpt, Mat& out, vector<uchar>& outliers, double ransacThreshold = 3.0, double confidence = 0.99)

Computes optimal affine transformation between two 3D point sets

Parameters:
  • srcpt – The first input 3D point set
  • dstpt – The second input 3D point set
  • out – The output 3D affine transformation matrix 3 \times 4
  • outliers – The output vector indicating which points are outliers
  • ransacThreshold – The maximum reprojection error in RANSAC algorithm to consider a point an inlier
  • confidence – The confidence level, between 0 and 1, with which the matrix is estimated

The function estimates the optimal 3D affine transformation between two 3D point sets using RANSAC algorithm.

cv::contourArea

Comments from the Wiki

double contourArea(const Mat& contour)

Calculates the contour area

Parameters:
  • contour – The contour vertices, represented by CV_32SC2 or CV_32FC2 matrix, or by vector<Point> or vector<Point2f> converted to the matrix using Mat(const vector<T>&) constructor.

The function computes the contour area. Similarly to moments() the area is computed using the Green formula, thus the returned area and the number of non-zero pixels, if you draw the contour using drawContours() or fillPoly() , can be different. Here is a short example:

vector<Point> contour;
contour.push_back(Point2f(0, 0));
contour.push_back(Point2f(10, 0));
contour.push_back(Point2f(10, 10));
contour.push_back(Point2f(5, 4));

double area0 = contourArea(contour);
vector<Point> approx;
approxPolyDP(contour, approx, 5, true);
double area1 = contourArea(approx);

cout << "area0 =" << area0 << endl <<
        "area1 =" << area1 << endl <<
        "approx poly vertices" << approx.size() << endl;

cv::convexHull

Comments from the Wiki

void convexHull(const Mat& points, vector<int>& hull, bool clockwise=false)
void convexHull(const Mat& points, vector<Point>& hull, bool clockwise=false)
void convexHull(const Mat& points, vector<Point2f>& hull, bool clockwise=false)

Finds the convex hull of a point set.

Parameters:
  • points – The input 2D point set, represented by CV_32SC2 or CV_32FC2 matrix, or by vector<Point> or vector<Point2f> converted to the matrix using Mat(const vector<T>&) constructor.
  • hull – The output convex hull. It is either a vector of points that form the hull (must have the same type as the input points), or a vector of 0-based point indices of the hull points in the original array (since the set of convex hull points is a subset of the original point set).
  • clockwise – If true, the output convex hull will be oriented clockwise, otherwise it will be oriented counter-clockwise. Here, the usual screen coordinate system is assumed - the origin is at the top-left corner, x axis is oriented to the right, and y axis is oriented downwards.

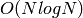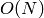The functions find the convex hull of a 2D point set using Sklansky’s algorithm Sklansky82 that has O(N logN) or O(N) complexity (where 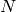N is the number of input points), depending on how the initial sorting is implemented (currently it is 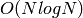O(N logN) . See the OpenCV sample convexhull.c that demonstrates the use of the different function variants.

cv::fitEllipse

Comments from the Wiki

RotatedRect fitEllipse(const Mat& points)

Fits an ellipse around a set of 2D points.

Parameters:
  • points – The input 2D point set, represented by CV_32SC2 or CV_32FC2 matrix, or by vector<Point> or vector<Point2f> converted to the matrix using Mat(const vector<T>&) constructor.

The function calculates the ellipse that fits best (in least-squares sense) a set of 2D points. It returns the rotated rectangle in which the ellipse is inscribed.

cv::fitLine

Comments from the Wiki

void fitLine(const Mat& points, Vec4f& line, int distType, double param, double reps, double aeps)
void fitLine(const Mat& points, Vec6f& line, int distType, double param, double reps, double aeps)

Fits a line to a 2D or 3D point set.

Parameters:
  • points – The input 2D point set, represented by CV_32SC2 or CV_32FC2 matrix, or by vector<Point> , vector<Point2f> , vector<Point3i> or vector<Point3f> converted to the matrix by Mat(const vector<T>&) constructor
  • line –

    The output line parameters. In the case of a 2d fitting, it is a vector of 4 floats ``(vx, vy,

    x0, y0)`` where (vx, vy) is a normalized vector collinear to the

    line and (x0, y0) is some point on the line. in the case of a 3D fitting it is vector of 6 floats (vx, vy, vz, x0, y0, z0) where (vx, vy, vz) is a normalized vector collinear to the line and (x0, y0, z0) is some point on the line

  • distType – The distance used by the M-estimator (see the discussion)
  • param – Numerical parameter ( C ) for some types of distances, if 0 then some optimal value is chosen
  • aeps (reps,) – Sufficient accuracy for the radius (distance between the coordinate origin and the line) and angle, respectively; 0.01 would be a good default value for both.

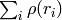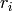The functions fitLine fit a line to a 2D or 3D point set by minimizing \sum_i \rho(r_i) where r_i is the distance between the 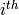i^{th} point and the line and 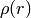\rho(r) is a distance function, one of:

  • distType=CV_DIST_L2

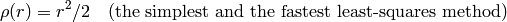
    \rho (r) = r^2/2 \quad \text{(the simplest and the fastest least-squares method)}

  • distType=CV_DIST_L1

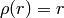
    \rho (r) = r

  • distType=CV_DIST_L12

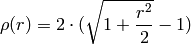
    \rho (r) = 2 \cdot ( \sqrt{1 + \frac{r^2}{2}} - 1)

  • distType=CV_DIST_FAIR

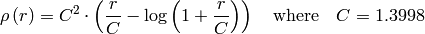
    \rho \left (r \right ) = C^2 \cdot \left ( \frac{r}{C} - \log{\left(1 + \frac{r}{C}\right)} \right ) \quad \text{where} \quad C=1.3998

  • distType=CV_DIST_WELSCH

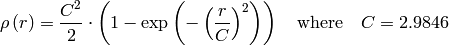
    \rho \left (r \right ) = \frac{C^2}{2} \cdot \left ( 1 - \exp{\left(-\left(\frac{r}{C}\right)^2\right)} \right ) \quad \text{where} \quad C=2.9846

  • distType=CV_DIST_HUBER

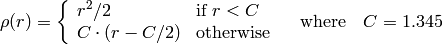
    \rho (r) = \fork{r^2/2}{if $r < C$}{C \cdot (r-C/2)}{otherwise} \quad \text{where} \quad C=1.345

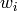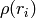The algorithm is based on the M-estimator ( http://en.wikipedia.org/wiki/M-estimator ) technique, that iteratively fits the line using weighted least-squares algorithm and after each iteration the weights w_i are adjusted to beinversely proportional to \rho(r_i) .

cv::isContourConvex

Comments from the Wiki

bool isContourConvex(const Mat& contour)

Tests contour convexity.

Parameters:
  • contour – The tested contour, a matrix of type CV_32SC2 or CV_32FC2 , or vector<Point> or vector<Point2f> converted to the matrix using Mat(const vector<T>&) constructor.

The function tests whether the input contour is convex or not. The contour must be simple, i.e. without self-intersections, otherwise the function output is undefined.

cv::minAreaRect

Comments from the Wiki

RotatedRect minAreaRect(const Mat& points)

Finds the minimum area rotated rectangle enclosing a 2D point set.

Parameters:
  • points – The input 2D point set, represented by CV_32SC2 or CV_32FC2 matrix, or by vector<Point> or vector<Point2f> converted to the matrix using Mat(const vector<T>&) constructor.

The function calculates and returns the minimum area bounding rectangle (possibly rotated) for the specified point set. See the OpenCV sample minarea.c

cv::minEnclosingCircle

Comments from the Wiki

void minEnclosingCircle(const Mat& points, Point2f& center, float& radius)

Finds the minimum area circle enclosing a 2D point set.

Parameters:
  • points – The input 2D point set, represented by CV_32SC2 or CV_32FC2 matrix, or by vector<Point> or vector<Point2f> converted to the matrix using Mat(const vector<T>&) constructor.
  • center – The output center of the circle
  • radius – The output radius of the circle

The function finds the minimal enclosing circle of a 2D point set using iterative algorithm. See the OpenCV sample minarea.c

cv::matchShapes

Comments from the Wiki

double matchShapes(const Mat& object1, const Mat& object2, int method, double parameter=0)

Compares two shapes.

Parameters:
  • object1 – The first contour or grayscale image
  • object2 – The second contour or grayscale image
  • method –
    Comparison method:
    CV_CONTOUR_MATCH_I1 , CV_CONTOURS_MATCH_I2
    or
    CV_CONTOURS_MATCH_I3 (see the discussion below)
  • parameter – Method-specific parameter (is not used now)

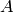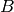The function compares two shapes. The 3 implemented methods all use Hu invariants (see HuMoments() ) as following ( A denotes object1 , B denotes object2 ):

  • method=CV_CONTOUR_MATCH_I1

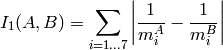
    I_1(A,B) = \sum _{i=1...7} \left | \frac{1}{m^A_i} - \frac{1}{m^B_i} \right |

  • method=CV_CONTOUR_MATCH_I2

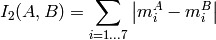
    I_2(A,B) = \sum _{i=1...7} \left | m^A_i - m^B_i \right |

  • method=CV_CONTOUR_MATCH_I3

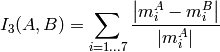
    I_3(A,B) = \sum _{i=1...7} \frac{ \left| m^A_i - m^B_i \right| }{ \left| m^A_i \right| }

where

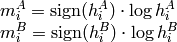
\begin{array}{l} m^A_i = \mathrm{sign} (h^A_i) \cdot \log{h^A_i} \\ m^B_i = \mathrm{sign} (h^B_i) \cdot \log{h^B_i} \end{array}

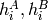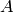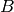and h^A_i, h^B_i are the Hu moments of A and B respectively.

cv::pointPolygonTest

Comments from the Wiki

double pointPolygonTest(const Mat& contour, Point2f pt, bool measureDist)

Performs point-in-contour test.

Parameters:
  • contour – The input contour
  • pt – The point tested against the contour
  • measureDist – If true, the function estimates the signed distance from the point to the nearest contour edge; otherwise, the function only checks if the point is inside or not.

The function determines whether the point is inside a contour, outside, or lies on an edge (or coincides with a vertex). It returns positive (inside), negative (outside) or zero (on an edge) value, correspondingly. When measureDist=false , the return value is +1, -1 and 0, respectively. Otherwise, the return value it is a signed distance between the point and the nearest contour edge.

Here is the sample output of the function, where each image pixel is tested against the contour.

_images/pointpolygon.png

Table Of Contents

Previous topic

Miscellaneous Image Transformations

Next topic

Planar Subdivisions

This Page

Navigation

© Copyright 2010, authors. Created using Sphinx 1.1pre.