Decision Trees¶
The ML classes discussed in this section implement Classification And Regression Tree algorithms, which are described in [Breiman84] .
The class CvDTree represents a single decision tree that may be used alone, or as a base class in tree ensembles (see Boosting and Random Trees ).
A decision tree is a binary tree (i.e. tree where each non-leaf node has exactly 2 child nodes). It can be used either for classification, when each tree leaf is marked with some class label (multiple leafs may have the same label), or for regression, when each tree leaf is also assigned a constant (so the approximation function is piecewise constant).
Predicting with Decision Trees¶
To reach a leaf node, and to obtain a response for the input feature vector, the prediction procedure starts with the root node. From each non-leaf node the procedure goes to the left (i.e. selects the left child node as the next observed node), or to the right based on the value of a certain variable, whose index is stored in the observed node. The variable can be either ordered or categorical. In the first case, the variable value is compared with the certain threshold (which is also stored in the node); if the value is less than the threshold, the procedure goes to the left, otherwise, to the right (for example, if the weight is less than 1 kilogram, the procedure goes to the left, else to the right). And in the second case the discrete variable value is tested to see if it belongs to a certain subset of values (also stored in the node) from a limited set of values the variable could take; if yes, the procedure goes to the left, else - to the right (for example, if the color is green or red, go to the left, else to the right). That is, in each node, a pair of entities (variable _ index, decision _ rule (threshold/subset)) is used. This pair is called a split (split on the variable variable _ index). Once a leaf node is reached, the value assigned to this node is used as the output of prediction procedure.
Sometimes, certain features of the input vector are missed (for example, in the darkness it is difficult to determine the object color), and the prediction procedure may get stuck in the certain node (in the mentioned example if the node is split by color). To avoid such situations, decision trees use so-called surrogate splits. That is, in addition to the best “primary” split, every tree node may also be split on one or more other variables with nearly the same results.
Training Decision Trees¶
The tree is built recursively, starting from the root node. All of the training data (feature vectors and the responses) is used to split the root node. In each node the optimum decision rule (i.e. the best “primary” split) is found based on some criteria (in ML gini “purity” criteria is used for classification, and sum of squared errors is used for regression). Then, if necessary, the surrogate splits are found that resemble the results of the primary split on the training data; all of the data is divided using the primary and the surrogate splits (just like it is done in the prediction procedure) between the left and the right child node. Then the procedure recursively splits both left and right nodes. At each node the recursive procedure may stop (i.e. stop splitting the node further) in one of the following cases:
- depth of the tree branch being constructed has reached the specified maximum value.
- number of training samples in the node is less than the specified threshold, when it is not statistically representative to split the node further.
- all the samples in the node belong to the same class (or, in the case of regression, the variation is too small).
- the best split found does not give any noticeable improvement compared to a random choice.
When the tree is built, it may be pruned using a cross-validation procedure, if necessary. That is, some branches of the tree that may lead to the model overfitting are cut off. Normally this procedure is only applied to standalone decision trees, while tree ensembles usually build small enough trees and use their own protection schemes against overfitting.
Variable importance¶
Besides the obvious use of decision trees - prediction, the tree can be also used for various data analysis. One of the key properties of the constructed decision tree algorithms is that it is possible to compute importance (relative decisive power) of each variable. For example, in a spam filter that uses a set of words occurred in the message as a feature vector, the variable importance rating can be used to determine the most “spam-indicating” words and thus help to keep the dictionary size reasonable.
Importance of each variable is computed over all the splits on this variable in the tree, primary and surrogate ones. Thus, to compute variable importance correctly, the surrogate splits must be enabled in the training parameters, even if there is no missing data.
[Breiman84] Breiman, L., Friedman, J. Olshen, R. and Stone, C. (1984), “Classification and Regression Trees”, Wadsworth.
CvDTreeSplit¶
- CvDTreeSplit¶
Decision tree node split.
struct CvDTreeSplit
{
int var_idx;
int inversed;
float quality;
CvDTreeSplit* next;
union
{
int subset[2];
struct
{
float c;
int split_point;
}
ord;
};
};
CvDTreeNode¶
- CvDTreeNode¶
Decision tree node.
struct CvDTreeNode
{
int class_idx;
int Tn;
double value;
CvDTreeNode* parent;
CvDTreeNode* left;
CvDTreeNode* right;
CvDTreeSplit* split;
int sample_count;
int depth;
...
};
Other numerous fields of CvDTreeNode are used internally at the training stage.
CvDTreeParams¶
- CvDTreeParams¶
Decision tree training parameters.
struct CvDTreeParams
{
int max_categories;
int max_depth;
int min_sample_count;
int cv_folds;
bool use_surrogates;
bool use_1se_rule;
bool truncate_pruned_tree;
float regression_accuracy;
const float* priors;
CvDTreeParams() : max_categories(10), max_depth(INT_MAX), min_sample_count(10),
cv_folds(10), use_surrogates(true), use_1se_rule(true),
truncate_pruned_tree(true), regression_accuracy(0.01f), priors(0)
{}
CvDTreeParams( int _max_depth, int _min_sample_count,
float _regression_accuracy, bool _use_surrogates,
int _max_categories, int _cv_folds,
bool _use_1se_rule, bool _truncate_pruned_tree,
const float* _priors );
};
The structure contains all the decision tree training parameters. There is a default constructor that initializes all the parameters with the default values tuned for standalone classification tree. Any of the parameters can be overridden then, or the structure may be fully initialized using the advanced variant of the constructor.
CvDTreeTrainData¶
- CvDTreeTrainData¶
Decision tree training data and shared data for tree ensembles.
struct CvDTreeTrainData
{
CvDTreeTrainData();
CvDTreeTrainData( const CvMat* _train_data, int _tflag,
const CvMat* _responses, const CvMat* _var_idx=0,
const CvMat* _sample_idx=0, const CvMat* _var_type=0,
const CvMat* _missing_mask=0,
const CvDTreeParams& _params=CvDTreeParams(),
bool _shared=false, bool _add_labels=false );
virtual ~CvDTreeTrainData();
virtual void set_data( const CvMat* _train_data, int _tflag,
const CvMat* _responses, const CvMat* _var_idx=0,
const CvMat* _sample_idx=0, const CvMat* _var_type=0,
const CvMat* _missing_mask=0,
const CvDTreeParams& _params=CvDTreeParams(),
bool _shared=false, bool _add_labels=false,
bool _update_data=false );
virtual void get_vectors( const CvMat* _subsample_idx,
float* values, uchar* missing, float* responses,
bool get_class_idx=false );
virtual CvDTreeNode* subsample_data( const CvMat* _subsample_idx );
virtual void write_params( CvFileStorage* fs );
virtual void read_params( CvFileStorage* fs, CvFileNode* node );
// release all the data
virtual void clear();
int get_num_classes() const;
int get_var_type(int vi) const;
int get_work_var_count() const;
virtual int* get_class_labels( CvDTreeNode* n );
virtual float* get_ord_responses( CvDTreeNode* n );
virtual int* get_labels( CvDTreeNode* n );
virtual int* get_cat_var_data( CvDTreeNode* n, int vi );
virtual CvPair32s32f* get_ord_var_data( CvDTreeNode* n, int vi );
virtual int get_child_buf_idx( CvDTreeNode* n );
////////////////////////////////////
virtual bool set_params( const CvDTreeParams& params );
virtual CvDTreeNode* new_node( CvDTreeNode* parent, int count,
int storage_idx, int offset );
virtual CvDTreeSplit* new_split_ord( int vi, float cmp_val,
int split_point, int inversed, float quality );
virtual CvDTreeSplit* new_split_cat( int vi, float quality );
virtual void free_node_data( CvDTreeNode* node );
virtual void free_train_data();
virtual void free_node( CvDTreeNode* node );
int sample_count, var_all, var_count, max_c_count;
int ord_var_count, cat_var_count;
bool have_labels, have_priors;
bool is_classifier;
int buf_count, buf_size;
bool shared;
CvMat* cat_count;
CvMat* cat_ofs;
CvMat* cat_map;
CvMat* counts;
CvMat* buf;
CvMat* direction;
CvMat* split_buf;
CvMat* var_idx;
CvMat* var_type; // i-th element =
// k<0 - ordered
// k>=0 - categorical, see k-th element of cat_* arrays
CvMat* priors;
CvDTreeParams params;
CvMemStorage* tree_storage;
CvMemStorage* temp_storage;
CvDTreeNode* data_root;
CvSet* node_heap;
CvSet* split_heap;
CvSet* cv_heap;
CvSet* nv_heap;
CvRNG rng;
};
This structure is mostly used internally for storing both standalone trees and tree ensembles efficiently. Basically, it contains 3 types of information:
- The training parameters, an instance of CvDTreeParams.
- The training data, preprocessed in order to find the best splits more efficiently. For tree ensembles this preprocessed data is reused by all the trees. Additionally, the training data characteristics that are shared by all trees in the ensemble are stored here: variable types, the number of classes, class label compression map etc.
- Buffers, memory storages for tree nodes, splits and other elements of the trees constructed.
There are 2 ways of using this structure. In simple cases (e.g. a standalone tree, or the ready-to-use “black box” tree ensemble from ML, like Random Trees or Boosting ) there is no need to care or even to know about the structure - just construct the needed statistical model, train it and use it. The CvDTreeTrainData structure will be constructed and used internally. However, for custom tree algorithms, or another sophisticated cases, the structure may be constructed and used explicitly. The scheme is the following:
- The structure is initialized using the default constructor, followed by set_data (or it is built using the full form of constructor). The parameter _shared must be set to true .
- One or more trees are trained using this data, see the special form of the method CvDTree::train .
- Finally, the structure can be released only after all the trees using it are released.
CvDTree¶
- CvDTree¶
Decision tree.
class CvDTree : public CvStatModel
{
public:
CvDTree();
virtual ~CvDTree();
virtual bool train( const CvMat* _train_data, int _tflag,
const CvMat* _responses, const CvMat* _var_idx=0,
const CvMat* _sample_idx=0, const CvMat* _var_type=0,
const CvMat* _missing_mask=0,
CvDTreeParams params=CvDTreeParams() );
virtual bool train( CvDTreeTrainData* _train_data,
const CvMat* _subsample_idx );
virtual CvDTreeNode* predict( const CvMat* _sample,
const CvMat* _missing_data_mask=0,
bool raw_mode=false ) const;
virtual const CvMat* get_var_importance();
virtual void clear();
virtual void read( CvFileStorage* fs, CvFileNode* node );
virtual void write( CvFileStorage* fs, const char* name );
// special read & write methods for trees in the tree ensembles
virtual void read( CvFileStorage* fs, CvFileNode* node,
CvDTreeTrainData* data );
virtual void write( CvFileStorage* fs );
const CvDTreeNode* get_root() const;
int get_pruned_tree_idx() const;
CvDTreeTrainData* get_data();
protected:
virtual bool do_train( const CvMat* _subsample_idx );
virtual void try_split_node( CvDTreeNode* n );
virtual void split_node_data( CvDTreeNode* n );
virtual CvDTreeSplit* find_best_split( CvDTreeNode* n );
virtual CvDTreeSplit* find_split_ord_class( CvDTreeNode* n, int vi );
virtual CvDTreeSplit* find_split_cat_class( CvDTreeNode* n, int vi );
virtual CvDTreeSplit* find_split_ord_reg( CvDTreeNode* n, int vi );
virtual CvDTreeSplit* find_split_cat_reg( CvDTreeNode* n, int vi );
virtual CvDTreeSplit* find_surrogate_split_ord( CvDTreeNode* n, int vi );
virtual CvDTreeSplit* find_surrogate_split_cat( CvDTreeNode* n, int vi );
virtual double calc_node_dir( CvDTreeNode* node );
virtual void complete_node_dir( CvDTreeNode* node );
virtual void cluster_categories( const int* vectors, int vector_count,
int var_count, int* sums, int k, int* cluster_labels );
virtual void calc_node_value( CvDTreeNode* node );
virtual void prune_cv();
virtual double update_tree_rnc( int T, int fold );
virtual int cut_tree( int T, int fold, double min_alpha );
virtual void free_prune_data(bool cut_tree);
virtual void free_tree();
virtual void write_node( CvFileStorage* fs, CvDTreeNode* node );
virtual void write_split( CvFileStorage* fs, CvDTreeSplit* split );
virtual CvDTreeNode* read_node( CvFileStorage* fs,
CvFileNode* node,
CvDTreeNode* parent );
virtual CvDTreeSplit* read_split( CvFileStorage* fs, CvFileNode* node );
virtual void write_tree_nodes( CvFileStorage* fs );
virtual void read_tree_nodes( CvFileStorage* fs, CvFileNode* node );
CvDTreeNode* root;
int pruned_tree_idx;
CvMat* var_importance;
CvDTreeTrainData* data;
};
CvDTree::train¶
- bool CvDTree::train(const CvMat* _train_data, int _tflag, const CvMat* _responses, const CvMat* _var_idx=0, const CvMat* _sample_idx=0, const CvMat* _var_type=0, const CvMat* _missing_mask=0, CvDTreeParams params=CvDTreeParams())¶
- bool CvDTree::train(CvDTreeTrainData* _train_data, const CvMat* _subsample_idx)
Trains a decision tree.
There are 2 train methods in CvDTree .
The first method follows the generic CvStatModel::train conventions, it is the most complete form. Both data layouts ( _tflag=CV_ROW_SAMPLE and _tflag=CV_COL_SAMPLE ) are supported, as well as sample and variable subsets, missing measurements, arbitrary combinations of input and output variable types etc. The last parameter contains all of the necessary training parameters, see the CvDTreeParams description.
The second method train is mostly used for building tree ensembles. It takes the pre-constructed CvDTreeTrainData instance and the optional subset of training set. The indices in _subsample_idx are counted relatively to the _sample_idx , passed to CvDTreeTrainData constructor. For example, if _sample_idx=[1, 5, 7, 100] , then _subsample_idx=[0,3] means that the samples [1, 100] of the original training set are used.
CvDTree::predict¶
- CvDTreeNode* CvDTree::predict(const CvMat* _sample, const CvMat* _missing_data_mask=0, bool raw_mode=false) const¶
Returns the leaf node of the decision tree corresponding to the input vector.
The method takes the feature vector and the optional missing measurement mask on input, traverses the decision tree and returns the reached leaf node on output. The prediction result, either the class label or the estimated function value, may be retrieved as the
value
field of the
CvDTreeNode
structure, for example: dtree-
 predict(sample,mask)-
predict(sample,mask)-
 value.
value.
The last parameter is normally set to
false
, implying a regular
input. If it is
true
, the method assumes that all the values of
the discrete input variables have been already normalized to
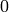 to
to
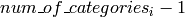 ranges. (as the decision tree uses such
normalized representation internally). It is useful for faster prediction
with tree ensembles. For ordered input variables the flag is not used.
ranges. (as the decision tree uses such
normalized representation internally). It is useful for faster prediction
with tree ensembles. For ordered input variables the flag is not used.
Example: Building A Tree for Classifying Mushrooms. See the mushroom.cpp sample that demonstrates how to build and use the decision tree.
Help and Feedback
You did not find what you were looking for?- Try the Cheatsheet.
- Ask a question in the user group/mailing list.
- If you think something is missing or wrong in the documentation, please file a bug report.
