ニューラルネットワーク¶

MLでは，フィードフォワードのニューラルネットワーク，より詳細に言えば，最も一般的に利用されるニューラルネットワークである多層パーセプトロン（MLP）が実装されています．MLPは，入力層，出力層，そして複数の中間層から構成されています．MLPの各層には，1つまたは複数のニューロンが存在し，それらは前後の層に存在するニューロンと一方向に連結されています．ここでは，3入力，2出力，中間層に5つのニューロンをもつ，3層パーセプトロンの例を示します：

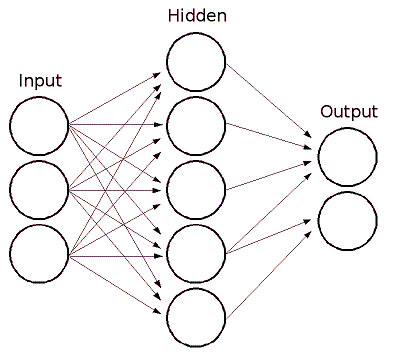
MLPのニューロンは，すべて似通ったものです．それぞれのニューロンは，複数の入力リンクをもち（つまり，前の層に属する複数のニューロンからの出力値を入力として受け取ります），複数の出力リンクをもちます（つまり，次の層に属する複数のニューロンへ出力値を渡します）．前の層から出力された値は，各ニューロン毎の重みを掛けて合計され，それにバイアス項が足されます．この合計値は，さらにニューロン毎に異なる活性化関数 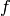$f$ によって変換されます．以下に，その図を示します：

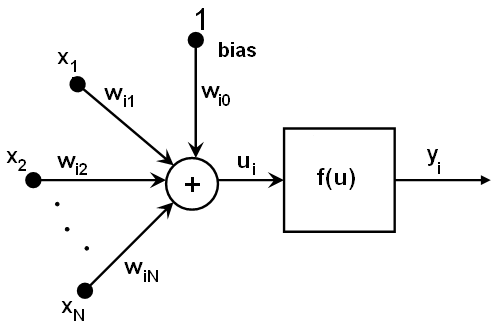
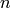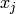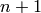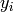言い換えれば，層 $n$ の出力 $x_j$ が与えられると，層 $n+1$ の出力 $y_i$ が次の用に求められます：

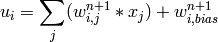
$u_i = \sum _j (w^{n+1}_{i,j}*x_j) + w^{n+1}_{i,bias}$

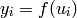
$y_i = f(u_i)$

MLでは，異なる活性化関数を利用した3つの標準的な実装がなされています：

恒等関数 ( CvANN_MLP::IDENTITY ): $f(x)=x$
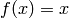
対称なシグモイド関数 ( CvANN_MLP::SIGMOID_SYM ): 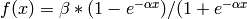$f(x)=\beta*(1-e^{-\alpha x})/(1+e^{-\alpha x}$ ), MLP のデフォルト値．標準的なシグモイド関数 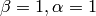$\beta =1, \alpha =1$ を以下に示します：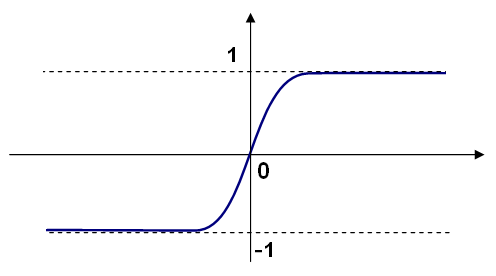
ガウス関数 ( CvANN_MLP::GAUSSIAN ): 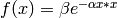$f(x)=\beta e^{-\alpha x*x}$ , 現時点では，完全にはサポートされていません．

MLでは，すべてのニューロンが同じ活性化関数を利用します．この活性化関数は，学習アルゴリズムによって変化しないユーザ指定のフリーパラメータ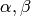（ $\alpha, \beta$ ）を共通してもちます．

学習済みのネットワークは次の様に動作します：ネットワークは入力として特徴ベクトルをとり，そのベクトルサイズは入力層と同じサイズです．それらの値が最初の中間層に入力として渡されると，重みと活性化関数を用いて中間層の出力が計算され，その値が，出力層の出力が求められるまで次々と下層に伝達されます．

したがって，ネットワークを構築するためには，すべての重み 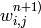$w^{n+1)}_{i,j}$ を知る必要があります．この重みは，学習アルゴリズムによって計算されます．アルゴリズムは，訓練集合（複数の入力ベクトルと，それに対応する出力ベクトル）を必要とし，与えられた入力ベクトルに対して期待通りの応答を出力するように，ネットワークの重みを繰り返し調整します．

ネットワークサイズ（中間層の層数と各層のサイズ）が大きくなればなるほど，ネットワークの柔軟性が増し，訓練集合における誤差を任意に小さくできるかもしれません．しかし同時に，この学習済みネットワークは訓練データに含まれるノイズも「学習」してしまい，通常，ネットワークサイズがある限界に達すると，訓練データに対する誤差も増加し始めます．さらに，大きなネットワークでは小さいものと比較して学習に相当な時間がかかるため，（ CalcPCA や，それに類似した手法を用いて）データの前処理を行い，本質的な特徴のみを用いて小さなネットワークを学習します．

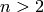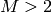MLPのもう1つの特徴として，カテゴリ変数をそのまま扱えない，というものがありますが，これには回避策が存在します．入力層や出力層におけるある特徴（つまり， $n>2$ の n -クラス分類器の場合）がカテゴリ変数であり， $M>2$ 個の異なる値を扱えるとします．これは，その特徴がとり得る M 個の値のうち i 番目の値と等しい場合にのみ i 番目の要素が1となるような， M 個の要素をもつ2値タプルで表現できます．これにより，入出力層のサイズは増加しますが，学習アルゴリズムは高速に収束するようになり，同時に，変数として「曖昧な」値，つまり，固定値の代わりに確率の組を使うということが可能になります．

MLには，MLPの学習のための2つのアルゴリズムが実装されています．1つは，古典的なランダム逐次誤差逆伝搬アルゴリズムであり，もう1つ（デフォルト）は，バッチRPROPアルゴリズムです．

参考文献：

http://en.wikipedia.org/wiki/Backpropagation . Wikipedia article about the back-propagation algorithm.
1. LeCun, L. Bottou, G.B. Orr and K.-R. Muller, “Efficient backprop”, in Neural Networks—Tricks of the Trade, Springer Lecture Notes in Computer Sciences 1524, pp.5-50, 1998.
1. Riedmiller and H. Braun, “A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP Algorithm”, Proc. ICNN, San Francisco (1993).

CvANN_MLP_TrainParams¶

CvANN_MLP_TrainParams¶

MLP学習アルゴリズムのパラメータ．

struct CvANN_MLP_TrainParams
{
    CvANN_MLP_TrainParams();
    CvANN_MLP_TrainParams( CvTermCriteria term_crit, int train_method,
                           double param1, double param2=0 );
    ~CvANN_MLP_TrainParams();

    enum { BACKPROP=0, RPROP=1 };

    CvTermCriteria term_crit;
    int train_method;

    // 誤差逆伝搬のパラメータ
    double bp_dw_scale, bp_moment_scale;

    // rprop のパラメータ
    double rp_dw0, rp_dw_plus, rp_dw_minus, rp_dw_min, rp_dw_max;
};

この構造体は， RPROP アルゴリズムのパラメータを初期化するデフォルトコンストラクタを持ちます．パラメータをカスタマイズでき，かつ/または，誤差逆伝搬アルゴリズムを選択できるような，より高度なコンストラクタも存在します．また，個々のパラメータは，この構造体が作成された後でも調整することができます．

CvANN_MLP¶

CvANN_MLP¶

MLPモデル．

class CvANN_MLP : public CvStatModel
{
public:
    CvANN_MLP();
    CvANN_MLP( const CvMat* _layer_sizes,
               int _activ_func=SIGMOID_SYM,
               double _f_param1=0, double _f_param2=0 );

    virtual ~CvANN_MLP();

    virtual void create( const CvMat* _layer_sizes,
                         int _activ_func=SIGMOID_SYM,
                         double _f_param1=0, double _f_param2=0 );

    virtual int train( const CvMat* _inputs, const CvMat* _outputs,
                       const CvMat* _sample_weights,
                       const CvMat* _sample_idx=0,
                       CvANN_MLP_TrainParams _params = CvANN_MLP_TrainParams(),
                       int flags=0 );
    virtual float predict( const CvMat* _inputs,
                           CvMat* _outputs ) const;

    virtual void clear();

    // 選択可能な活性化関数
    enum { IDENTITY = 0, SIGMOID_SYM = 1, GAUSSIAN = 2 };

    // 利用可能な学習フラグ
    enum { UPDATE_WEIGHTS = 1, NO_INPUT_SCALE = 2, NO_OUTPUT_SCALE = 4 };

    virtual void read( CvFileStorage* fs, CvFileNode* node );
    virtual void write( CvFileStorage* storage, const char* name );

    int get_layer_count() { return layer_sizes ? layer_sizes->cols : 0; }
    const CvMat* get_layer_sizes() { return layer_sizes; }

protected:

    virtual bool prepare_to_train( const CvMat* _inputs, const CvMat* _outputs,
            const CvMat* _sample_weights, const CvMat* _sample_idx,
            CvANN_MLP_TrainParams _params,
            CvVectors* _ivecs, CvVectors* _ovecs, double** _sw, int _flags );

    // 逐次的ランダム誤差逆伝搬
    virtual int train_backprop( CvVectors _ivecs, CvVectors _ovecs,
                                                const double* _sw );

    // RPROPアルゴリズム
    virtual int train_rprop( CvVectors _ivecs, CvVectors _ovecs,
                                             const double* _sw );

    virtual void calc_activ_func( CvMat* xf, const double* bias ) const;
    virtual void calc_activ_func_deriv( CvMat* xf, CvMat* deriv,
                                             const double* bias ) const;
    virtual void set_activ_func( int _activ_func=SIGMOID_SYM,
                                 double _f_param1=0, double _f_param2=0 );
    virtual void init_weights();
    virtual void scale_input( const CvMat* _src, CvMat* _dst ) const;
    virtual void scale_output( const CvMat* _src, CvMat* _dst ) const;
    virtual void calc_input_scale( const CvVectors* vecs, int flags );
    virtual void calc_output_scale( const CvVectors* vecs, int flags );

    virtual void write_params( CvFileStorage* fs );
    virtual void read_params( CvFileStorage* fs, CvFileNode* node );

    CvMat* layer_sizes;
    CvMat* wbuf;
    CvMat* sample_weights;
    double** weights;
    double f_param1, f_param2;
    double min_val, max_val, min_val1, max_val1;
    int activ_func;
    int max_count, max_buf_sz;
    CvANN_MLP_TrainParams params;
    CvRNG rng;
};

モデルの構築と学習を一度に行うMLの他のモデルとは異なり，MLPモデルではこれらの2つのステップは別々のものです．まず最初に，デフォルトではないコンストラクタか， create メソッドを用いて，指定されたトポロジーを持つネットワークを構成します．このとき，全ての重みは0にセットされます．そして，入出力ベクトルの組を用いて，このネットワークを学習します．学習処理は，1度以上繰り返されます．つまり，新しい学習データが来る度に重みが調整されます．

cv::CvANN_MLP::create¶

void CvANN_MLP::create(const CvMat* _layer_sizes, int _activ_func=SIGMOID_SYM, double _f_param1=0, double _f_param2=0)¶

指定されたトポロジーを持つMLPを作成します．

パラメタ:

_layer_sizes – 入出力層を含む各層のニューロン数を指定する整数ベクトル
_activ_func – 各ニューロンに対する活性化関数の指定． CvANN_MLP::IDENTITY , CvANN_MLP::SIGMOID_SYM および CvANN_MLP::GAUSSIAN のいずれか
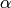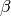_f_param1,_f_param2 – 活性化関数のフリーパラメータ $\alpha$ と $\beta$ ．イントロダクションのセクションの式を参照してください

このメソッドは，指定されたトポロジーを持つMLPネットワークを作成し，全てのニューロンに対して同じ活性化関数を割り当てます．

cv::CvANN_MLP::train¶

int CvANN_MLP::train(const CvMat* _inputs, const CvMat* _outputs, const CvMat* _sample_weights, const CvMat* _sample_idx=0, CvANN_MLP_TrainParams _params = CvANN_MLP_TrainParams(), int flags=0)¶

MLPを学習/更新します．

パラメタ:

_inputs – 入力ベクトルで構成される，浮動小数点型の行列．1ベクトルが1行を構成します
_outputs – 対応する出力ベクトルで構成される，浮動小数点型の行列．1ベクトルが1行を構成します
_sample_weights – オプション．（RPROPの場合のみ）各サンプルに対する重みで構成される，浮動小数点型のベクトル．学習時に他のサンプルよりも重要なサンプルがあると，hit-rate と false-alarm rate のバランスを適切に保つために，あるクラスの重みを上げたい場合があります
_sample_idx – オプション．サンプルを表す整数型ベクトル（つまり， _inputs と _outputs の両方の行が考慮されます）
_params – 学習パラメータ． CvANN_MLP_TrainParams の説明を参照してください
_flags –
学習アルゴリズムを制御するための様々なパラメータ．以下の値の組み合わせ：
- UPDATE_WEIGHTS = 1 アルゴリズムは，ネットワークの重みを最初から計算し直さずに，更新を行います（最初から計算する場合は， Nguyen-Widrow アルゴリズムを用いて重みを初期化します）
- NO_INPUT_SCALE アルゴリズムは，入力ベクトルを正規化しません．このフラグがセットされていない場合，学習アルゴリズムは，平均が0，標準偏差が1になるように各入力特徴を個別に正規化します．もしネットワークが頻繁に更新されるならば，新しい学習データは元々のデータと大きく異なっているのかもしれません．この場合，ユーザは適切な正規化を行う必要があります
- NO_OUTPUT_SCALE アルゴリズムは，出力ベクトルを正規化しません．このフラグがセットされていない場合，学習アルゴリズムは，使われている活性化関数に依存するある範囲内に収まるように，各出力特徴を個別に正規化します

このメソッドは，指定された学習アルゴリズムを用いてネットワークの重みを計算/更新します．これは，計算の反復数を返します．

ニューラルネットワーク¶

CvANN_MLP_TrainParams¶

CvANN_MLP¶

cv::CvANN_MLP::create¶

cv::CvANN_MLP::train¶

ヘルプとフィードバック

目次

前のトピックへ

次のトピックへ

このページ

ナビゲーション

ニューラルネットワーク¶

CvANN_MLP_TrainParams¶

CvANN_MLP¶

cv::CvANN_MLP::create¶

cv::CvANN_MLP::train¶

ヘルプとフィードバック

目次

前のトピックへ

次のトピックへ

このページ

クイック検索

ナビゲーション