Image Filtering¶
Functions and classes described in this section are used to perform various linear or non-linear filtering operations on 2D images (represented as
Mat()
‘s), that is, for each pixel location
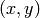 in the source image some its (normally rectangular) neighborhood is considered and used to compute the response. In case of a linear filter it is a weighted sum of pixel values, in case of morphological operations it is the minimum or maximum etc. The computed response is stored to the destination image at the same location
in the source image some its (normally rectangular) neighborhood is considered and used to compute the response. In case of a linear filter it is a weighted sum of pixel values, in case of morphological operations it is the minimum or maximum etc. The computed response is stored to the destination image at the same location
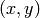 . It means, that the output image will be of the same size as the input image. Normally, the functions supports multi-channel arrays, in which case every channel is processed independently, therefore the output image will also have the same number of channels as the input one.
. It means, that the output image will be of the same size as the input image. Normally, the functions supports multi-channel arrays, in which case every channel is processed independently, therefore the output image will also have the same number of channels as the input one.
Another common feature of the functions and classes described in this section is that, unlike simple arithmetic functions, they need to extrapolate values of some non-existing pixels. For example, if we want to smooth an image using a Gaussian
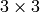 filter, then during the processing of the left-most pixels in each row we need pixels to the left of them, i.e. outside of the image. We can let those pixels be the same as the left-most image pixels (i.e. use “replicated border” extrapolation method), or assume that all the non-existing pixels are zeros (“contant border” extrapolation method) etc.
OpenCV let the user to specify the extrapolation method; see the function borderInterpolate() and discussion of borderType parameter in various functions below.
filter, then during the processing of the left-most pixels in each row we need pixels to the left of them, i.e. outside of the image. We can let those pixels be the same as the left-most image pixels (i.e. use “replicated border” extrapolation method), or assume that all the non-existing pixels are zeros (“contant border” extrapolation method) etc.
OpenCV let the user to specify the extrapolation method; see the function borderInterpolate() and discussion of borderType parameter in various functions below.
BaseColumnFilter¶
- BaseColumnFilter¶
Base class for filters with single-column kernels
class BaseColumnFilter
{
public:
virtual ~BaseColumnFilter();
// To be overriden by the user.
//
// runs filtering operation on the set of rows,
// "dstcount + ksize - 1" rows on input,
// "dstcount" rows on output,
// each input and output row has "width" elements
// the filtered rows are written into "dst" buffer.
virtual void operator()(const uchar** src, uchar* dst, int dststep,
int dstcount, int width) = 0;
// resets the filter state (may be needed for IIR filters)
virtual void reset();
int ksize; // the aperture size
int anchor; // position of the anchor point,
// normally not used during the processing
};
The class BaseColumnFilter is the base class for filtering data using single-column kernels. The filtering does not have to be a linear operation. In general, it could be written as following:
, \; \texttt{src} [y+1](x), \; ..., \; \texttt{src} [y+ \texttt{ksize} -1](x)](_images/math/283057407b1837ae0c58ce608ff39ba6dfabab9c.png)
where
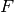 is the filtering function, but, as it is represented as a class, it can produce any side effects, memorize previously processed data etc. The class only defines the interface and is not used directly. Instead, there are several functions in OpenCV (and you can add more) that return pointers to the derived classes that implement specific filtering operations. Those pointers are then passed to
FilterEngine()
constructor. While the filtering operation interface uses
uchar
type, a particular implementation is not limited to 8-bit data.
is the filtering function, but, as it is represented as a class, it can produce any side effects, memorize previously processed data etc. The class only defines the interface and is not used directly. Instead, there are several functions in OpenCV (and you can add more) that return pointers to the derived classes that implement specific filtering operations. Those pointers are then passed to
FilterEngine()
constructor. While the filtering operation interface uses
uchar
type, a particular implementation is not limited to 8-bit data.
See also: BaseRowFilter() , BaseFilter() , FilterEngine() ,
getColumnSumFilter() , getLinearColumnFilter() , getMorphologyColumnFilter()
BaseFilter¶
- BaseFilter¶
Base class for 2D image filters
class BaseFilter
{
public:
virtual ~BaseFilter();
// To be overriden by the user.
//
// runs filtering operation on the set of rows,
// "dstcount + ksize.height - 1" rows on input,
// "dstcount" rows on output,
// each input row has "(width + ksize.width-1)*cn" elements
// each output row has "width*cn" elements.
// the filtered rows are written into "dst" buffer.
virtual void operator()(const uchar** src, uchar* dst, int dststep,
int dstcount, int width, int cn) = 0;
// resets the filter state (may be needed for IIR filters)
virtual void reset();
Size ksize;
Point anchor;
};
The class BaseFilter is the base class for filtering data using 2D kernels. The filtering does not have to be a linear operation. In general, it could be written as following:
, \; \texttt{src} [y](x+1), \; ..., \; \texttt{src} [y](x+ \texttt{ksize.width} -1), \\ \texttt{src} [y+1](x), \; \texttt{src} [y+1](x+1), \; ..., \; \texttt{src} [y+1](x+ \texttt{ksize.width} -1), \\ ......................................................................................... \\ \texttt{src} [y+ \texttt{ksize.height-1} ](x), \\ \texttt{src} [y+ \texttt{ksize.height-1} ](x+1), \\ ...
\texttt{src} [y+ \texttt{ksize.height-1} ](x+ \texttt{ksize.width} -1))
\end{array}](_images/math/7154f919653e0e8e27c44e70dd0f9bd384d15346.png)
where
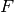 is the filtering function. The class only defines the interface and is not used directly. Instead, there are several functions in OpenCV (and you can add more) that return pointers to the derived classes that implement specific filtering operations. Those pointers are then passed to
FilterEngine()
constructor. While the filtering operation interface uses
uchar
type, a particular implementation is not limited to 8-bit data.
is the filtering function. The class only defines the interface and is not used directly. Instead, there are several functions in OpenCV (and you can add more) that return pointers to the derived classes that implement specific filtering operations. Those pointers are then passed to
FilterEngine()
constructor. While the filtering operation interface uses
uchar
type, a particular implementation is not limited to 8-bit data.
See also: BaseColumnFilter() , BaseRowFilter() , FilterEngine() ,
BaseRowFilter¶
- BaseRowFilter¶
Base class for filters with single-row kernels
class BaseRowFilter
{
public:
virtual ~BaseRowFilter();
// To be overriden by the user.
//
// runs filtering operation on the single input row
// of "width" element, each element is has "cn" channels.
// the filtered row is written into "dst" buffer.
virtual void operator()(const uchar* src, uchar* dst,
int width, int cn) = 0;
int ksize, anchor;
};
The class BaseRowFilter is the base class for filtering data using single-row kernels. The filtering does not have to be a linear operation. In general, it could be written as following:
, \; \texttt{src} [y](x+1), \; ..., \; \texttt{src} [y](x+ \texttt{ksize.width} -1))](_images/math/7fff1eee21140adda2558a63fb40d93e598cef91.png)
where
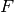 is the filtering function. The class only defines the interface and is not used directly. Instead, there are several functions in OpenCV (and you can add more) that return pointers to the derived classes that implement specific filtering operations. Those pointers are then passed to
FilterEngine()
constructor. While the filtering operation interface uses
uchar
type, a particular implementation is not limited to 8-bit data.
is the filtering function. The class only defines the interface and is not used directly. Instead, there are several functions in OpenCV (and you can add more) that return pointers to the derived classes that implement specific filtering operations. Those pointers are then passed to
FilterEngine()
constructor. While the filtering operation interface uses
uchar
type, a particular implementation is not limited to 8-bit data.
See also: BaseColumnFilter() , Filter() , FilterEngine() ,
getLinearRowFilter() , getMorphologyRowFilter() , getRowSumFilter()
FilterEngine¶
- FilterEngine¶
Generic image filtering class
class FilterEngine
{
public:
// empty constructor
FilterEngine();
// builds a 2D non-separable filter (!_filter2D.empty()) or
// a separable filter (!_rowFilter.empty() && !_columnFilter.empty())
// the input data type will be "srcType", the output data type will be "dstType",
// the intermediate data type is "bufType".
// _rowBorderType and _columnBorderType determine how the image
// will be extrapolated beyond the image boundaries.
// _borderValue is only used when _rowBorderType and/or _columnBorderType
// == cv::BORDER_CONSTANT
FilterEngine(const Ptr<BaseFilter>& _filter2D,
const Ptr<BaseRowFilter>& _rowFilter,
const Ptr<BaseColumnFilter>& _columnFilter,
int srcType, int dstType, int bufType,
int _rowBorderType=BORDER_REPLICATE,
int _columnBorderType=-1, // use _rowBorderType by default
const Scalar& _borderValue=Scalar());
virtual ~FilterEngine();
// separate function for the engine initialization
void init(const Ptr<BaseFilter>& _filter2D,
const Ptr<BaseRowFilter>& _rowFilter,
const Ptr<BaseColumnFilter>& _columnFilter,
int srcType, int dstType, int bufType,
int _rowBorderType=BORDER_REPLICATE, int _columnBorderType=-1,
const Scalar& _borderValue=Scalar());
// starts filtering of the ROI in an image of size "wholeSize".
// returns the starting y-position in the source image.
virtual int start(Size wholeSize, Rect roi, int maxBufRows=-1);
// alternative form of start that takes the image
// itself instead of "wholeSize". Set isolated to true to pretend that
// there are no real pixels outside of the ROI
// (so that the pixels will be extrapolated using the specified border modes)
virtual int start(const Mat& src, const Rect& srcRoi=Rect(0,0,-1,-1),
bool isolated=false, int maxBufRows=-1);
// processes the next portion of the source image,
// "srcCount" rows starting from "src" and
// stores the results to "dst".
// returns the number of produced rows
virtual int proceed(const uchar* src, int srcStep, int srcCount,
uchar* dst, int dstStep);
// higher-level function that processes the whole
// ROI or the whole image with a single call
virtual void apply( const Mat& src, Mat& dst,
const Rect& srcRoi=Rect(0,0,-1,-1),
Point dstOfs=Point(0,0),
bool isolated=false);
bool isSeparable() const { return filter2D.empty(); }
// how many rows from the input image are not yet processed
int remainingInputRows() const;
// how many output rows are not yet produced
int remainingOutputRows() const;
...
// the starting and the ending rows in the source image
int startY, endY;
// pointers to the filters
Ptr<BaseFilter> filter2D;
Ptr<BaseRowFilter> rowFilter;
Ptr<BaseColumnFilter> columnFilter;
};
The class FilterEngine can be used to apply an arbitrary filtering operation to an image. It contains all the necessary intermediate buffers, it computes extrapolated values of the “virtual” pixels outside of the image etc. Pointers to the initialized FilterEngine instances are returned by various create*Filter functions, see below, and they are used inside high-level functions such as filter2D() , erode() , dilate() etc, that is, the class is the workhorse in many of OpenCV filtering functions.
This class makes it easier (though, maybe not very easy yet) to combine filtering operations with other operations, such as color space conversions, thresholding, arithmetic operations, etc. By combining several operations together you can get much better performance because your data will stay in cache. For example, below is the implementation of Laplace operator for a floating-point images, which is a simplified implementation of Laplacian() :
void laplace_f(const Mat& src, Mat& dst)
{
CV_Assert( src.type() == CV_32F );
dst.create(src.size(), src.type());
// get the derivative and smooth kernels for d2I/dx2.
// for d2I/dy2 we could use the same kernels, just swapped
Mat kd, ks;
getSobelKernels( kd, ks, 2, 0, ksize, false, ktype );
// let's process 10 source rows at once
int DELTA = std::min(10, src.rows);
Ptr<FilterEngine> Fxx = createSeparableLinearFilter(src.type(),
dst.type(), kd, ks, Point(-1,-1), 0, borderType, borderType, Scalar() );
Ptr<FilterEngine> Fyy = createSeparableLinearFilter(src.type(),
dst.type(), ks, kd, Point(-1,-1), 0, borderType, borderType, Scalar() );
int y = Fxx->start(src), dsty = 0, dy = 0;
Fyy->start(src);
const uchar* sptr = src.data + y*src.step;
// allocate the buffers for the spatial image derivatives;
// the buffers need to have more than DELTA rows, because at the
// last iteration the output may take max(kd.rows-1,ks.rows-1)
// rows more than the input.
Mat Ixx( DELTA + kd.rows - 1, src.cols, dst.type() );
Mat Iyy( DELTA + kd.rows - 1, src.cols, dst.type() );
// inside the loop we always pass DELTA rows to the filter
// (note that the "proceed" method takes care of possibe overflow, since
// it was given the actual image height in the "start" method)
// on output we can get:
// * < DELTA rows (the initial buffer accumulation stage)
// * = DELTA rows (settled state in the middle)
// * > DELTA rows (then the input image is over, but we generate
// "virtual" rows using the border mode and filter them)
// this variable number of output rows is dy.
// dsty is the current output row.
// sptr is the pointer to the first input row in the portion to process
for( ; dsty < dst.rows; sptr += DELTA*src.step, dsty += dy )
{
Fxx->proceed( sptr, (int)src.step, DELTA, Ixx.data, (int)Ixx.step );
dy = Fyy->proceed( sptr, (int)src.step, DELTA, d2y.data, (int)Iyy.step );
if( dy > 0 )
{
Mat dstripe = dst.rowRange(dsty, dsty + dy);
add(Ixx.rowRange(0, dy), Iyy.rowRange(0, dy), dstripe);
}
}
}
If you do not need that much control of the filtering process, you can simply use the FilterEngine::apply method. Here is how the method is actually implemented:
void FilterEngine::apply(const Mat& src, Mat& dst,
const Rect& srcRoi, Point dstOfs, bool isolated)
{
// check matrix types
CV_Assert( src.type() == srcType && dst.type() == dstType );
// handle the "whole image" case
Rect _srcRoi = srcRoi;
if( _srcRoi == Rect(0,0,-1,-1) )
_srcRoi = Rect(0,0,src.cols,src.rows);
// check if the destination ROI is inside the dst.
// and FilterEngine::start will check if the source ROI is inside src.
CV_Assert( dstOfs.x >= 0 && dstOfs.y >= 0 &&
dstOfs.x + _srcRoi.width <= dst.cols &&
dstOfs.y + _srcRoi.height <= dst.rows );
// start filtering
int y = start(src, _srcRoi, isolated);
// process the whole ROI. Note that "endY - startY" is the total number
// of the source rows to process
// (including the possible rows outside of srcRoi but inside the source image)
proceed( src.data + y*src.step,
(int)src.step, endY - startY,
dst.data + dstOfs.y*dst.step +
dstOfs.x*dst.elemSize(), (int)dst.step );
}
Unlike the earlier versions of OpenCV, now the filtering operations fully support the notion of image ROI, that is, pixels outside of the ROI but inside the image can be used in the filtering operations. For example, you can take a ROI of a single pixel and filter it - that will be a filter response at that particular pixel (however, it’s possible to emulate the old behavior by passing isolated=false to FilterEngine::start or FilterEngine::apply ). You can pass the ROI explicitly to FilterEngine::apply , or construct a new matrix headers:
// compute dI/dx derivative at src(x,y)
// method 1:
// form a matrix header for a single value
float val1 = 0;
Mat dst1(1,1,CV_32F,&val1);
Ptr<FilterEngine> Fx = createDerivFilter(CV_32F, CV_32F,
1, 0, 3, BORDER_REFLECT_101);
Fx->apply(src, Rect(x,y,1,1), Point(), dst1);
// method 2:
// form a matrix header for a single value
float val2 = 0;
Mat dst2(1,1,CV_32F,&val2);
Mat pix_roi(src, Rect(x,y,1,1));
Sobel(pix_roi, dst2, dst2.type(), 1, 0, 3, 1, 0, BORDER_REFLECT_101);
printf("method1 =
Note on the data types. As it was mentioned in BaseFilter() description, the specific filters can process data of any type, despite that Base*Filter::operator() only takes uchar pointers and no information about the actual types. To make it all work, the following rules are used:
- in case of separable filtering FilterEngine::rowFilter applied first. It transforms the input image data (of type srcType ) to the intermediate results stored in the internal buffers (of type bufType ). Then these intermediate results are processed as single-channel data with FilterEngine::columnFilter and stored in the output image (of type dstType ). Thus, the input type for rowFilter is srcType and the output type is bufType ; the input type for columnFilter is CV_MAT_DEPTH(bufType) and the output type is CV_MAT_DEPTH(dstType) .
- in case of non-separable filtering bufType must be the same as srcType . The source data is copied to the temporary buffer if needed and then just passed to FilterEngine::filter2D . That is, the input type for filter2D is srcType (= bufType ) and the output type is dstType .
See also: BaseColumnFilter() , BaseFilter() , BaseRowFilter() , createBoxFilter() , createDerivFilter() , createGaussianFilter() , createLinearFilter() , createMorphologyFilter() , createSeparableLinearFilter()
cv::bilateralFilter¶
- void bilateralFilter(const Mat& src, Mat& dst, int d, double sigmaColor, double sigmaSpace, int borderType=BORDER_DEFAULT)¶
Applies bilateral filter to the image
Parameters: - src – The source 8-bit or floating-point, 1-channel or 3-channel image
- dst – The destination image; will have the same size and the same type as src
- d – The diameter of each pixel neighborhood, that is used during filtering. If it is non-positive, it’s computed from sigmaSpace
- sigmaColor – Filter sigma in the color space. Larger value of the parameter means that farther colors within the pixel neighborhood (see sigmaSpace ) will be mixed together, resulting in larger areas of semi-equal color
- sigmaSpace – Filter sigma in the coordinate space. Larger value of the parameter means that farther pixels will influence each other (as long as their colors are close enough; see sigmaColor ). Then d>0 , it specifies the neighborhood size regardless of sigmaSpace , otherwise d is proportional to sigmaSpace
The function applies bilateral filtering to the input image, as described in http://www.dai.ed.ac.uk/CVonline/LOCAL_COPIES/MANDUCHI1/Bilateral_Filtering.html
cv::blur¶
- void blur(const Mat& src, Mat& dst, Size ksize, Point anchor=Point(-1, -1), int borderType=BORDER_DEFAULT)¶
Smoothes image using normalized box filter
Parameters: - src – The source image
- dst – The destination image; will have the same size and the same type as src
- ksize – The smoothing kernel size
- anchor – The anchor point. The default value Point(-1,-1) means that the anchor is at the kernel center
- borderType – The border mode used to extrapolate pixels outside of the image
The function smoothes the image using the kernel:
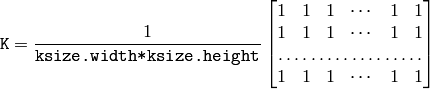
The call blur(src, dst, ksize, anchor, borderType) is equivalent to boxFilter(src, dst, src.type(), anchor, true, borderType) .
See also: boxFilter() , bilateralFilter() , GaussianBlur() , medianBlur() .
cv::borderInterpolate¶
- int borderInterpolate(int p, int len, int borderType)¶
Computes source location of extrapolated pixel
Parameters: - p – 0-based coordinate of the extrapolated pixel along one of the axes, likely <0 or >= len
- len – length of the array along the corresponding axis
- borderType – the border type, one of the BORDER_* , except for BORDER_TRANSPARENT and BORDER_ISOLATED . When borderType==BORDER_CONSTANT the function always returns -1, regardless of p and len
The function computes and returns the coordinate of the donor pixel, corresponding to the specified extrapolated pixel when using the specified extrapolation border mode. For example, if we use BORDER_WRAP mode in the horizontal direction, BORDER_REFLECT_101 in the vertical direction and want to compute value of the “virtual” pixel Point(-5, 100) in a floating-point image img , it will be
float val = img.at<float>(borderInterpolate(100, img.rows, BORDER_REFLECT_101),
borderInterpolate(-5, img.cols, BORDER_WRAP));
Normally, the function is not called directly; it is used inside FilterEngine() and copyMakeBorder() to compute tables for quick extrapolation.
See also: FilterEngine() , copyMakeBorder()
cv::boxFilter¶
- void boxFilter(const Mat& src, Mat& dst, int ddepth, Size ksize, Point anchor=Point(-1, -1), bool normalize=true, int borderType=BORDER_DEFAULT)¶
Smoothes image using box filter
Parameters: - src – The source image
- dst – The destination image; will have the same size and the same type as src
- ksize – The smoothing kernel size
- anchor – The anchor point. The default value Point(-1,-1) means that the anchor is at the kernel center
- normalize – Indicates, whether the kernel is normalized by its area or not
- borderType – The border mode used to extrapolate pixels outside of the image
The function smoothes the image using the kernel:
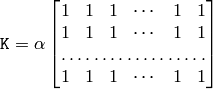
where

Unnormalized box filter is useful for computing various integral characteristics over each pixel neighborhood, such as covariation matrices of image derivatives (used in dense optical flow algorithms, etc.). If you need to compute pixel sums over variable-size windows, use integral() .
See also: boxFilter() , bilateralFilter() , GaussianBlur() , medianBlur() , integral() .
cv::buildPyramid¶
- void buildPyramid(const Mat& src, vector<Mat>& dst, int maxlevel)¶
Constructs Gaussian pyramid for an image
Parameters: - src – The source image; check pyrDown() for the list of supported types
- dst – The destination vector of maxlevel+1 images of the same type as src ; dst[0] will be the same as src , dst[1] is the next pyramid layer, a smoothed and down-sized src etc.
- maxlevel – The 0-based index of the last (i.e. the smallest) pyramid layer; it must be non-negative
The function constructs a vector of images and builds the gaussian pyramid by recursively applying pyrDown() to the previously built pyramid layers, starting from dst[0]==src .
cv::copyMakeBorder¶
- void copyMakeBorder(const Mat& src, Mat& dst, int top, int bottom, int left, int right, int borderType, const Scalar& value=Scalar())¶
Forms a border around the image
Parameters: - src – The source image
- dst – The destination image; will have the same type as src and the size Size(src.cols+left+right, src.rows+top+bottom)
- top, bottom, left, right – Specify how much pixels in each direction from the source image rectangle one needs to extrapolate, e.g. top=1, bottom=1, left=1, right=1 mean that 1 pixel-wide border needs to be built
- borderType – The border type; see borderInterpolate()
- value – The border value if borderType==BORDER_CONSTANT
The function copies the source image into the middle of the destination image. The areas to the left, to the right, above and below the copied source image will be filled with extrapolated pixels. This is not what FilterEngine() or based on it filtering functions do (they extrapolate pixels on-fly), but what other more complex functions, including your own, may do to simplify image boundary handling.
The function supports the mode when src is already in the middle of dst . In this case the function does not copy src itself, but simply constructs the border, e.g.:
// let border be the same in all directions
int border=2;
// constructs a larger image to fit both the image and the border
Mat gray_buf(rgb.rows + border*2, rgb.cols + border*2, rgb.depth());
// select the middle part of it w/o copying data
Mat gray(gray_canvas, Rect(border, border, rgb.cols, rgb.rows));
// convert image from RGB to grayscale
cvtColor(rgb, gray, CV_RGB2GRAY);
// form a border in-place
copyMakeBorder(gray, gray_buf, border, border,
border, border, BORDER_REPLICATE);
// now do some custom filtering ...
...
See also: borderInterpolate()
cv::createBoxFilter¶
- Ptr<FilterEngine> createBoxFilter(int srcType, int dstType, Size ksize, Point anchor=Point(-1, -1), bool normalize=true, int borderType=BORDER_DEFAULT)¶
- Ptr<BaseRowFilter> getRowSumFilter(int srcType, int sumType, int ksize, int anchor=-1)¶
- Ptr<BaseColumnFilter> getColumnSumFilter(int sumType, int dstType, int ksize, int anchor=-1, double scale=1)¶
Returns box filter engine
Parameters: - srcType – The source image type
- sumType – The intermediate horizontal sum type; must have as many channels as srcType
- dstType – The destination image type; must have as many channels as srcType
- ksize – The aperture size
- anchor – The anchor position with the kernel; negative values mean that the anchor is at the kernel center
- normalize – Whether the sums are normalized or not; see boxFilter()
- scale – Another way to specify normalization in lower-level getColumnSumFilter
- borderType – Which border type to use; see borderInterpolate()
The function is a convenience function that retrieves horizontal sum primitive filter with getRowSumFilter() , vertical sum filter with getColumnSumFilter() , constructs new FilterEngine() and passes both of the primitive filters there. The constructed filter engine can be used for image filtering with normalized or unnormalized box filter.
The function itself is used by blur() and boxFilter() .
See also: FilterEngine() , blur() , boxFilter() .
cv::createDerivFilter¶
- Ptr<FilterEngine> createDerivFilter(int srcType, int dstType, int dx, int dy, int ksize, int borderType=BORDER_DEFAULT)¶
Returns engine for computing image derivatives
Parameters: - srcType – The source image type
- dstType – The destination image type; must have as many channels as srcType
- dx – The derivative order in respect with x
- dy – The derivative order in respect with y
- ksize – The aperture size; see getDerivKernels()
- borderType – Which border type to use; see borderInterpolate()
The function createDerivFilter() is a small convenience function that retrieves linear filter coefficients for computing image derivatives using getDerivKernels() and then creates a separable linear filter with createSeparableLinearFilter() . The function is used by Sobel() and Scharr() .
See also: createSeparableLinearFilter() , getDerivKernels() , Scharr() , Sobel() .
cv::createGaussianFilter¶
- Ptr<FilterEngine> createGaussianFilter(int type, Size ksize, double sigmaX, double sigmaY=0, int borderType=BORDER_DEFAULT)¶
Returns engine for smoothing images with a Gaussian filter
Parameters: - type – The source and the destination image type
- ksize – The aperture size; see getGaussianKernel()
- sigmaX – The Gaussian sigma in the horizontal direction; see getGaussianKernel()
- sigmaY – The Gaussian sigma in the vertical direction; if 0, then
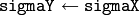
- borderType – Which border type to use; see borderInterpolate()
The function createGaussianFilter() computes Gaussian kernel coefficients and then returns separable linear filter for that kernel. The function is used by GaussianBlur() . Note that while the function takes just one data type, both for input and output, you can pass by this limitation by calling getGaussianKernel() and then createSeparableFilter() directly.
See also: createSeparableLinearFilter() , getGaussianKernel() , GaussianBlur() .
cv::createLinearFilter¶
- Ptr<FilterEngine> createLinearFilter(int srcType, int dstType, const Mat& kernel, Point _anchor=Point(-1, -1), double delta=0, int rowBorderType=BORDER_DEFAULT, int columnBorderType=-1, const Scalar& borderValue=Scalar())¶
- Ptr<BaseFilter> getLinearFilter(int srcType, int dstType, const Mat& kernel, Point anchor=Point(-1, -1), double delta=0, int bits=0)¶
Creates non-separable linear filter engine
Parameters: - srcType – The source image type
- dstType – The destination image type; must have as many channels as srcType
- kernel – The 2D array of filter coefficients
- anchor – The anchor point within the kernel; special value Point(-1,-1) means that the anchor is at the kernel center
- delta – The value added to the filtered results before storing them
- bits – When the kernel is an integer matrix representing fixed-point filter coefficients, the parameter specifies the number of the fractional bits
- rowBorderType, columnBorderType – The pixel extrapolation methods in the horizontal and the vertical directions; see borderInterpolate()
- borderValue – Used in case of constant border
The function returns pointer to 2D linear filter for the specified kernel, the source array type and the destination array type. The function is a higher-level function that calls getLinearFilter and passes the retrieved 2D filter to FilterEngine() constructor.
See also: createSeparableLinearFilter() , FilterEngine() , filter2D()
cv::createMorphologyFilter¶
- Ptr<FilterEngine> createMorphologyFilter(int op, int type, const Mat& element, Point anchor=Point(-1, -1), int rowBorderType=BORDER_CONSTANT, int columnBorderType=-1, const Scalar& borderValue=morphologyDefaultBorderValue())¶
- Ptr<BaseFilter> getMorphologyFilter(int op, int type, const Mat& element, Point anchor=Point(-1, -1))¶
- Ptr<BaseRowFilter> getMorphologyRowFilter(int op, int type, int esize, int anchor=-1)¶
- Ptr<BaseColumnFilter> getMorphologyColumnFilter(int op, int type, int esize, int anchor=-1)¶
- static inline Scalar morphologyDefaultBorderValue(){ return Scalar::all(DBL_MAX) }
Creates engine for non-separable morphological operations
Parameters: - op – The morphology operation id, MORPH_ERODE or MORPH_DILATE
- type – The input/output image type
- element – The 2D 8-bit structuring element for the morphological operation. Non-zero elements indicate the pixels that belong to the element
- esize – The horizontal or vertical structuring element size for separable morphological operations
- anchor – The anchor position within the structuring element; negative values mean that the anchor is at the center
- rowBorderType, columnBorderType – The pixel extrapolation methods in the horizontal and the vertical directions; see borderInterpolate()
- borderValue – The border value in case of a constant border. The default value, morphologyDefaultBorderValue , has the special meaning. It is transformed
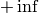 for the erosion and to
for the erosion and to 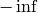 for the dilation, which means that the minimum (maximum) is effectively computed only over the pixels that are inside the image.
for the dilation, which means that the minimum (maximum) is effectively computed only over the pixels that are inside the image.
The functions construct primitive morphological filtering operations or a filter engine based on them. Normally it’s enough to use createMorphologyFilter() or even higher-level erode() , dilate() or morphologyEx() , Note, that createMorphologyFilter() analyses the structuring element shape and builds a separable morphological filter engine when the structuring element is square.
See also: erode() , dilate() , morphologyEx() , FilterEngine()
cv::createSeparableLinearFilter¶
- Ptr<FilterEngine> createSeparableLinearFilter(int srcType, int dstType, const Mat& rowKernel, const Mat& columnKernel, Point anchor=Point(-1, -1), double delta=0, int rowBorderType=BORDER_DEFAULT, int columnBorderType=-1, const Scalar& borderValue=Scalar())¶
- Ptr<BaseColumnFilter> getLinearColumnFilter(int bufType, int dstType, const Mat& columnKernel, int anchor, int symmetryType, double delta=0, int bits=0)¶
- Ptr<BaseRowFilter> getLinearRowFilter(int srcType, int bufType, const Mat& rowKernel, int anchor, int symmetryType)¶
Creates engine for separable linear filter
Parameters: - srcType – The source array type
- dstType – The destination image type; must have as many channels as srcType
- bufType – The inermediate buffer type; must have as many channels as srcType
- rowKernel – The coefficients for filtering each row
- columnKernel – The coefficients for filtering each column
- anchor – The anchor position within the kernel; negative values mean that anchor is positioned at the aperture center
- delta – The value added to the filtered results before storing them
- bits – When the kernel is an integer matrix representing fixed-point filter coefficients, the parameter specifies the number of the fractional bits
- rowBorderType, columnBorderType – The pixel extrapolation methods in the horizontal and the vertical directions; see borderInterpolate()
- borderValue – Used in case of a constant border
- symmetryType – The type of each of the row and column kernel; see getKernelType() .
The functions construct primitive separable linear filtering operations or a filter engine based on them. Normally it’s enough to use createSeparableLinearFilter() or even higher-level sepFilter2D() . The function createMorphologyFilter() is smart enough to figure out the symmetryType for each of the two kernels, the intermediate bufType , and, if the filtering can be done in integer arithmetics, the number of bits to encode the filter coefficients. If it does not work for you, it’s possible to call getLinearColumnFilter , getLinearRowFilter directly and then pass them to FilterEngine() constructor.
See also: sepFilter2D() , createLinearFilter() , FilterEngine() , getKernelType()
cv::dilate¶
- void dilate(const Mat& src, Mat& dst, const Mat& element, Point anchor=Point(-1, -1), int iterations=1, int borderType=BORDER_CONSTANT, const Scalar& borderValue=morphologyDefaultBorderValue())¶
Dilates an image by using a specific structuring element.
Parameters: - src – The source image
- dst – The destination image. It will have the same size and the same type as src
- element – The structuring element used for dilation. If element=Mat() , a
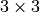 rectangular structuring element is used
rectangular structuring element is used - anchor – Position of the anchor within the element. The default value
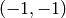 means that the anchor is at the element center
means that the anchor is at the element center - iterations – The number of times dilation is applied
- borderType – The pixel extrapolation method; see borderInterpolate()
- borderValue – The border value in case of a constant border. The default value has a special meaning, see createMorphologyFilter()
The function dilates the source image using the specified structuring element that determines the shape of a pixel neighborhood over which the maximum is taken:
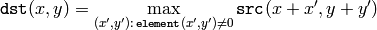
The function supports the in-place mode. Dilation can be applied several ( iterations ) times. In the case of multi-channel images each channel is processed independently.
See also: erode() , morphologyEx() , createMorphologyFilter()
cv::erode¶
- void erode(const Mat& src, Mat& dst, const Mat& element, Point anchor=Point(-1, -1), int iterations=1, int borderType=BORDER_CONSTANT, const Scalar& borderValue=morphologyDefaultBorderValue())¶
Erodes an image by using a specific structuring element.
Parameters: - src – The source image
- dst – The destination image. It will have the same size and the same type as src
- element – The structuring element used for dilation. If element=Mat() , a
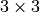 rectangular structuring element is used
rectangular structuring element is used - anchor – Position of the anchor within the element. The default value
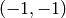 means that the anchor is at the element center
means that the anchor is at the element center - iterations – The number of times erosion is applied
- borderType – The pixel extrapolation method; see borderInterpolate()
- borderValue – The border value in case of a constant border. The default value has a special meaning, see createMorphoogyFilter()
The function erodes the source image using the specified structuring element that determines the shape of a pixel neighborhood over which the minimum is taken:
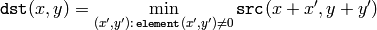
The function supports the in-place mode. Erosion can be applied several ( iterations ) times. In the case of multi-channel images each channel is processed independently.
See also: dilate() , morphologyEx() , createMorphologyFilter()
cv::filter2D¶
- void filter2D(const Mat& src, Mat& dst, int ddepth, const Mat& kernel, Point anchor=Point(-1, -1), double delta=0, int borderType=BORDER_DEFAULT)¶
Convolves an image with the kernel
Parameters: - src – The source image
- dst – The destination image. It will have the same size and the same number of channels as src
- ddepth – The desired depth of the destination image. If it is negative, it will be the same as src.depth()
- kernel – Convolution kernel (or rather a correlation kernel), a single-channel floating point matrix. If you want to apply different kernels to different channels, split the image into separate color planes using split() and process them individually
- anchor – The anchor of the kernel that indicates the relative position of a filtered point within the kernel. The anchor should lie within the kernel. The special default value (-1,-1) means that the anchor is at the kernel center
- delta – The optional value added to the filtered pixels before storing them in dst
- borderType – The pixel extrapolation method; see borderInterpolate()
The function applies an arbitrary linear filter to the image. In-place operation is supported. When the aperture is partially outside the image, the function interpolates outlier pixel values according to the specified border mode.
The function does actually computes correlation, not the convolution:
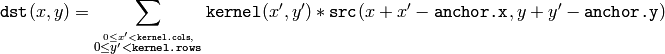
That is, the kernel is not mirrored around the anchor point. If you need a real convolution, flip the kernel using flip() and set the new anchor to (kernel.cols - anchor.x - 1, kernel.rows - anchor.y - 1) .
The function uses
-based algorithm in case of sufficiently large kernels (~
 ) and the direct algorithm (that uses the engine retrieved by
createLinearFilter()
) for small kernels.
) and the direct algorithm (that uses the engine retrieved by
createLinearFilter()
) for small kernels.
See also: sepFilter2D() , createLinearFilter() , dft() , matchTemplate()
cv::GaussianBlur¶
- void GaussianBlur(const Mat& src, Mat& dst, Size ksize, double sigmaX, double sigmaY=0, int borderType=BORDER_DEFAULT)¶
Smoothes image using a Gaussian filter
Parameters: - src – The source image
- dst – The destination image; will have the same size and the same type as src
- ksize – The Gaussian kernel size; ksize.width and ksize.height can differ, but they both must be positive and odd. Or, they can be zero’s, then they are computed from sigma*
- sigmaX, sigmaY – The Gaussian kernel standard deviations in X and Y direction. If sigmaY is zero, it is set to be equal to sigmaX . If they are both zeros, they are computed from ksize.width and ksize.height , respectively, see getGaussianKernel() . To fully control the result regardless of possible future modification of all this semantics, it is recommended to specify all of ksize , sigmaX and sigmaY
- borderType – The pixel extrapolation method; see borderInterpolate()
The function convolves the source image with the specified Gaussian kernel. In-place filtering is supported.
See also: sepFilter2D() , filter2D() , blur() , boxFilter() , bilateralFilter() , medianBlur()
cv::getDerivKernels¶
- void getDerivKernels(Mat& kx, Mat& ky, int dx, int dy, int ksize, bool normalize=false, int ktype=CV_32F)¶
Returns filter coefficients for computing spatial image derivatives
Parameters: - kx – The output matrix of row filter coefficients; will have type ktype
- ky – The output matrix of column filter coefficients; will have type ktype
- dx – The derivative order in respect with x
- dy – The derivative order in respect with y
- ksize – The aperture size. It can be CV_SCHARR , 1, 3, 5 or 7
- normalize – Indicates, whether to normalize (scale down) the filter coefficients or not. In theory the coefficients should have the denominator
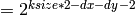 . If you are going to filter floating-point images, you will likely want to use the normalized kernels. But if you compute derivatives of a 8-bit image, store the results in 16-bit image and wish to preserve all the fractional bits, you may want to set normalize=false .
. If you are going to filter floating-point images, you will likely want to use the normalized kernels. But if you compute derivatives of a 8-bit image, store the results in 16-bit image and wish to preserve all the fractional bits, you may want to set normalize=false . - ktype – The type of filter coefficients. It can be CV_32f or CV_64F
The function computes and returns the filter coefficients for spatial image derivatives. When
ksize=CV_SCHARR
, the Scharr
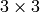 kernels are generated, see
Scharr()
. Otherwise, Sobel kernels are generated, see
Sobel()
. The filters are normally passed to
sepFilter2D()
or to
createSeparableLinearFilter()
.
kernels are generated, see
Scharr()
. Otherwise, Sobel kernels are generated, see
Sobel()
. The filters are normally passed to
sepFilter2D()
or to
createSeparableLinearFilter()
.
cv::getGaussianKernel¶
- Mat getGaussianKernel(int ksize, double sigma, int ktype=CV_64F)¶
Returns Gaussian filter coefficients
Parameters: - ksize – The aperture size. It should be odd (
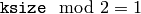 ) and positive.
) and positive. - sigma – The Gaussian standard deviation. If it is non-positive, it is computed from ksize as sigma = 0.3*(ksize/2 - 1) + 0.8
- ktype – The type of filter coefficients. It can be CV_32f or CV_64F
- ksize – The aperture size. It should be odd (
The function computes and returns the
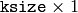 matrix of Gaussian filter coefficients:
matrix of Gaussian filter coefficients:
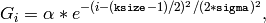
where
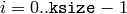 and
and
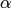 is the scale factor chosen so that
is the scale factor chosen so that
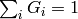 Two of such generated kernels can be passed to
sepFilter2D()
or to
createSeparableLinearFilter()
that will automatically detect that these are smoothing kernels and handle them accordingly. Also you may use the higher-level
GaussianBlur()
.
Two of such generated kernels can be passed to
sepFilter2D()
or to
createSeparableLinearFilter()
that will automatically detect that these are smoothing kernels and handle them accordingly. Also you may use the higher-level
GaussianBlur()
.
See also: sepFilter2D() , createSeparableLinearFilter() , getDerivKernels() , getStructuringElement() , GaussianBlur() .
cv::getKernelType¶
- int getKernelType(const Mat& kernel, Point anchor)¶
Returns the kernel type
Parameters: - kernel – 1D array of the kernel coefficients to analyze
- anchor – The anchor position within the kernel
The function analyzes the kernel coefficients and returns the corresponding kernel type:
- KERNEL_GENERAL Generic kernel - when there is no any type of symmetry or other properties
- KERNEL_SYMMETRICAL The kernel is symmetrical:
and the anchor is at the center
- KERNEL_ASYMMETRICAL The kernel is asymmetrical:
and the anchor is at the center
- KERNEL_SMOOTH All the kernel elements are non-negative and sum to 1. E.g. the Gaussian kernel is both smooth kernel and symmetrical, so the function will return KERNEL_SMOOTH | KERNEL_SYMMETRICAL
- KERNEL_INTEGER Al the kernel coefficients are integer numbers. This flag can be combined with KERNEL_SYMMETRICAL or KERNEL_ASYMMETRICAL
cv::getStructuringElement¶
- Mat getStructuringElement(int shape, Size esize, Point anchor=Point(-1, -1))¶
Returns the structuring element of the specified size and shape for morphological operations
Parameters: - shape –
The element shape, one of:
- MORPH_RECT - rectangular structuring element
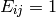
- MORPH_ELLIPSE - elliptic structuring element, i.e. a filled
- ellipse inscribed into the rectangle
- Rect(0, 0, esize.width, 0.esize.height)
- MORPH_CROSS - cross-shaped structuring element:
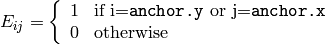
- MORPH_RECT - rectangular structuring element
- esize – Size of the structuring element
- anchor – The anchor position within the element. The default value
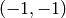 means that the anchor is at the center. Note that only the cross-shaped element’s shape depends on the anchor position; in other cases the anchor just regulates by how much the result of the morphological operation is shifted
means that the anchor is at the center. Note that only the cross-shaped element’s shape depends on the anchor position; in other cases the anchor just regulates by how much the result of the morphological operation is shifted
- shape –
The function constructs and returns the structuring element that can be then passed to createMorphologyFilter() , erode() , dilate() or morphologyEx() . But also you can construct an arbitrary binary mask yourself and use it as the structuring element.
cv::medianBlur¶
- void medianBlur(const Mat& src, Mat& dst, int ksize)¶
Smoothes image using median filter
Parameters: - src – The source 1-, 3- or 4-channel image. When ksize is 3 or 5, the image depth should be CV_8U , CV_16U or CV_32F . For larger aperture sizes it can only be CV_8U
- dst – The destination array; will have the same size and the same type as src
- ksize – The aperture linear size. It must be odd and more than 1, i.e. 3, 5, 7 ...
The function smoothes image using the median filter with
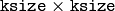 aperture. Each channel of a multi-channel image is processed independently. In-place operation is supported.
aperture. Each channel of a multi-channel image is processed independently. In-place operation is supported.
See also: bilateralFilter() , blur() , boxFilter() , GaussianBlur()
cv::morphologyEx¶
- void morphologyEx(const Mat& src, Mat& dst, int op, const Mat& element, Point anchor=Point(-1, -1), int iterations=1, int borderType=BORDER_CONSTANT, const Scalar& borderValue=morphologyDefaultBorderValue())¶
Performs advanced morphological transformations
Parameters: - src – Source image
- dst – Destination image. It will have the same size and the same type as src
- element – Structuring element
- op –
Type of morphological operation, one of the following:
- MORPH_OPEN opening
- MORPH_CLOSE closing
- MORPH_GRADIENT morphological gradient
- MORPH_TOPHAT “top hat”
- MORPH_BLACKHAT “black hat”
- iterations – Number of times erosion and dilation are applied
- borderType – The pixel extrapolation method; see borderInterpolate()
- borderValue – The border value in case of a constant border. The default value has a special meaning, see createMorphoogyFilter()
The function can perform advanced morphological transformations using erosion and dilation as basic operations.
Opening:
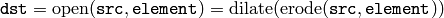
Closing:
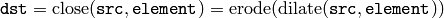
Morphological gradient:
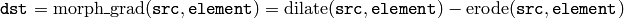
“Top hat”:
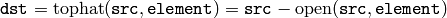
“Black hat”:
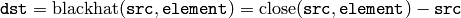
Any of the operations can be done in-place.
See also: dilate() , erode() , createMorphologyFilter()
cv::Laplacian¶
- void Laplacian(const Mat& src, Mat& dst, int ddepth, int ksize=1, double scale=1, double delta=0, int borderType=BORDER_DEFAULT)¶
Calculates the Laplacian of an image
Parameters: - src – Source image
- dst – Destination image; will have the same size and the same number of channels as src
- ddepth – The desired depth of the destination image
- ksize – The aperture size used to compute the second-derivative filters, see getDerivKernels() . It must be positive and odd
- scale – The optional scale factor for the computed Laplacian values (by default, no scaling is applied, see getDerivKernels() )
- delta – The optional delta value, added to the results prior to storing them in dst
- borderType – The pixel extrapolation method, see borderInterpolate()
The function calculates the Laplacian of the source image by adding up the second x and y derivatives calculated using the Sobel operator:
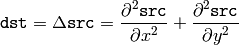
This is done when
ksize > 1
. When
ksize == 1
, the Laplacian is computed by filtering the image with the following
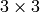 aperture:
aperture:
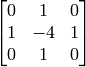
cv::pyrDown¶
- void pyrDown(const Mat& src, Mat& dst, const Size& dstsize=Size())¶
Smoothes an image and downsamples it.
Parameters: - src – The source image
- dst – The destination image. It will have the specified size and the same type as src
- dstsize –
Size of the destination image. By default it is computed as Size((src.cols+1)/2, (src.rows+1)/2) . But in any case the following conditions should be satisfied:
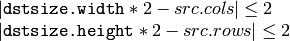
The function performs the downsampling step of the Gaussian pyramid construction. First it convolves the source image with the kernel:

and then downsamples the image by rejecting even rows and columns.
cv::pyrUp¶
- void pyrUp(const Mat& src, Mat& dst, const Size& dstsize=Size())¶
Upsamples an image and then smoothes it
Parameters: - src – The source image
- dst – The destination image. It will have the specified size and the same type as src
- dstsize –
Size of the destination image. By default it is computed as Size(src.cols*2, (src.rows*2) . But in any case the following conditions should be satisfied:
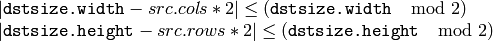
The function performs the upsampling step of the Gaussian pyramid construction (it can actually be used to construct the Laplacian pyramid). First it upsamples the source image by injecting even zero rows and columns and then convolves the result with the same kernel as in pyrDown() , multiplied by 4.
cv::sepFilter2D¶
- void sepFilter2D(const Mat& src, Mat& dst, int ddepth, const Mat& rowKernel, const Mat& columnKernel, Point anchor=Point(-1, -1), double delta=0, int borderType=BORDER_DEFAULT)¶
Applies separable linear filter to an image
Parameters: - src – The source image
- dst – The destination image; will have the same size and the same number of channels as src
- ddepth – The destination image depth
- rowKernel – The coefficients for filtering each row
- columnKernel – The coefficients for filtering each column
- anchor – The anchor position within the kernel; The default value
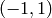 means that the anchor is at the kernel center
means that the anchor is at the kernel center - delta – The value added to the filtered results before storing them
- borderType – The pixel extrapolation method; see borderInterpolate()
The function applies a separable linear filter to the image. That is, first, every row of src is filtered with 1D kernel rowKernel . Then, every column of the result is filtered with 1D kernel columnKernel and the final result shifted by delta is stored in dst .
See also: createSeparableLinearFilter() , filter2D() , Sobel() , GaussianBlur() , boxFilter() , blur() .
cv::Sobel¶
- void Sobel(const Mat& src, Mat& dst, int ddepth, int xorder, int yorder, int ksize=3, double scale=1, double delta=0, int borderType=BORDER_DEFAULT)¶
Calculates the first, second, third or mixed image derivatives using an extended Sobel operator
Parameters: - src – The source image
- dst – The destination image; will have the same size and the same number of channels as src
- ddepth – The destination image depth
- xorder – Order of the derivative x
- yorder – Order of the derivative y
- ksize – Size of the extended Sobel kernel, must be 1, 3, 5 or 7
- scale – The optional scale factor for the computed derivative values (by default, no scaling is applied, see getDerivKernels() )
- delta – The optional delta value, added to the results prior to storing them in dst
- borderType – The pixel extrapolation method, see borderInterpolate()
In all cases except 1, an
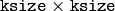 separable kernel will be used to calculate the
derivative. When
separable kernel will be used to calculate the
derivative. When
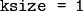 , a
, a
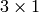 or
or
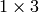 kernel will be used (i.e. no Gaussian smoothing is done).
ksize = 1
can only be used for the first or the second x- or y- derivatives.
kernel will be used (i.e. no Gaussian smoothing is done).
ksize = 1
can only be used for the first or the second x- or y- derivatives.
There is also the special value
ksize = CV_SCHARR
(-1) that corresponds to a
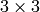 Scharr
filter that may give more accurate results than a
Scharr
filter that may give more accurate results than a
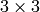 Sobel. The Scharr
aperture is
Sobel. The Scharr
aperture is
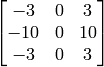
for the x-derivative or transposed for the y-derivative.
The function calculates the image derivative by convolving the image with the appropriate kernel:
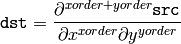
The Sobel operators combine Gaussian smoothing and differentiation, so the result is more or less resistant to the noise. Most often, the function is called with ( xorder = 1, yorder = 0, ksize = 3) or ( xorder = 0, yorder = 1, ksize = 3) to calculate the first x- or y- image derivative. The first case corresponds to a kernel of:
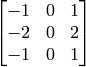
and the second one corresponds to a kernel of:
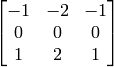
See also: Scharr() , Lapacian() , sepFilter2D() , filter2D() , GaussianBlur()
cv::Scharr¶
- void Scharr(const Mat& src, Mat& dst, int ddepth, int xorder, int yorder, double scale=1, double delta=0, int borderType=BORDER_DEFAULT)¶
Calculates the first x- or y- image derivative using Scharr operator
Parameters: - src – The source image
- dst – The destination image; will have the same size and the same number of channels as src
- ddepth – The destination image depth
- xorder – Order of the derivative x
- yorder – Order of the derivative y
- scale – The optional scale factor for the computed derivative values (by default, no scaling is applied, see getDerivKernels() )
- delta – The optional delta value, added to the results prior to storing them in dst
- borderType – The pixel extrapolation method, see borderInterpolate()
The function computes the first x- or y- spatial image derivative using Scharr operator. The call
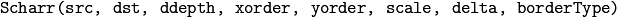
is equivalent to
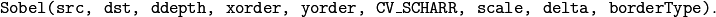
Help and Feedback
You did not find what you were looking for?- Try the FAQ.
- Ask a question in the user group/mailing list.
- If you think something is missing or wrong in the documentation, please file a bug report.
