カメラキャリブレーションと3次元再構成¶
このセクションで述べる関数は,いわゆるピンホールカメラモデルを取り扱います.つまりこのモデルでは,3次元座点を透視投影変換を用いて画像平面に射影することで,シーンのビューが構成されています.
![s \; m' = A [R|t] M'](_images/math/765aba62c7cb09fd36c1b44f3a2e422a28c4ec70.png)
または
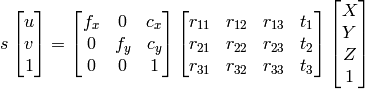
ここで
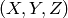 はワールド座標系の3次元座標を表し
はワールド座標系の3次元座標を表し
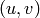 は画像平面に投影された点の座標を表します.
は画像平面に投影された点の座標を表します.
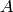 は,カメラ行列,またはカメラの内部パラメータ行列と呼ばれます.
は,カメラ行列,またはカメラの内部パラメータ行列と呼ばれます.
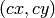 は主点(通常は画像中心),
は主点(通常は画像中心),
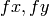 はピクセル単位で表される焦点距離です.
したがって,あるファクタによってカメラ画像がスケーリングされている場合,
このすべてのパラメータを同じファクタでスケーリング(それぞれが,拡大または縮小)する必要があります.
内部パラメータ行列はビューに依存しないので,一度推定すれば(ズームレンズの場合)焦点距離を固定している限りは繰返し使用することができます.
並進-回転の同次変換行列である
はピクセル単位で表される焦点距離です.
したがって,あるファクタによってカメラ画像がスケーリングされている場合,
このすべてのパラメータを同じファクタでスケーリング(それぞれが,拡大または縮小)する必要があります.
内部パラメータ行列はビューに依存しないので,一度推定すれば(ズームレンズの場合)焦点距離を固定している限りは繰返し使用することができます.
並進-回転の同次変換行列である
![[R|t]](_images/math/2ec354f9c8316cb3d69be8ceb97c53180a29640e.png) は,外部パラメータ行列と呼ばれます.
これは,静的環境に対するカメラの動き,または逆に,固定カメラの前の物体の剛体運動を表します.
つまり
は,外部パラメータ行列と呼ばれます.
これは,静的環境に対するカメラの動き,または逆に,固定カメラの前の物体の剛体運動を表します.
つまり
![[R|t]](_images/math/2ec354f9c8316cb3d69be8ceb97c53180a29640e.png) は,点座標
は,点座標
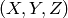 をそれぞれのカメラの座標系に変換します.
上述の変換は,以下の式(で
をそれぞれのカメラの座標系に変換します.
上述の変換は,以下の式(で
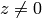 の場合)と等価です.
の場合)と等価です.
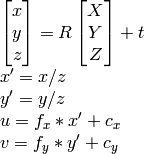
実際のカメラレンズは,主に半径方向の歪みや,わずかに円周方向の歪みを持っているので,上のモデルは以下のように拡張されます.
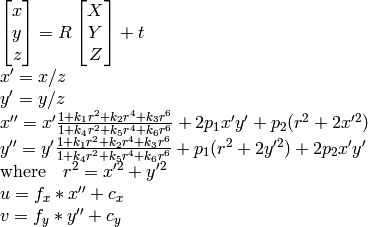
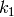 ,
,
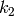 ,
,
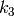 ,
,
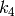 ,
,
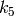 ,
,
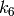 は半径方向の歪み係数,
は半径方向の歪み係数,
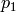 ,
,
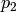 は円周方向の歪み係数です.
OpenCV では高次の係数は考慮されません.以降の関数では,歪み係数は
は円周方向の歪み係数です.
OpenCV では高次の係数は考慮されません.以降の関数では,歪み係数は
![(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6]])](_images/math/78ac305a1dc11b5dbdcdc8908bcc4fffc2d6d729.png)
というベクトルとして,渡されたり返されたりします.つまり,ベクトルが4つの要素をもつならば,
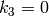 であることを意味します.
歪み係数はシーンのビューに依存しないので,カメラの内部パラメータに属します.
また,キャプチャされた画像の解像度に関わらず同じ値のままになります.
つまり,例えば,あるカメラが
であることを意味します.
歪み係数はシーンのビューに依存しないので,カメラの内部パラメータに属します.
また,キャプチャされた画像の解像度に関わらず同じ値のままになります.
つまり,例えば,あるカメラが
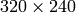 の画像でキャリブレーションされた場合,同じカメラの
の画像でキャリブレーションされた場合,同じカメラの
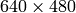 の画像に対してもまったく同じ歪み係数を用いることができます
(
の画像に対してもまったく同じ歪み係数を用いることができます
(
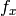 ,
,
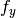 ,
,
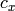 ,
,
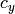 は適切にスケーリングされなければいけませんが).
は適切にスケーリングされなければいけませんが).
以降の関数は,このようなモデルを用いて,次のようなことを行います:
- 内部パラメータ,外部パラメータが与えられた場合に,3次元座標を画像平面上に投影します.
- 内部パラメータ,少数の3次元点,その投影点が与えられた場合に,外部パラメータを求めます.
- 既知のキャリブレーションパターンを写した複数のビュー(つまり,各ビューが,複数の3次元点と2次元点の対応として記述できます)から,カメラの内部パラメータ,外部パラメータを推定します.
- ステレオカメラ「ヘッド」の相対位置と相対姿勢を推定し,カメラの光軸を平行にする 平行化 変換を求めます.
CalcImageHomography¶
- void cvCalcImageHomography(float* line, CvPoint3D32f* center, float* intrinsic, float* homography)¶
楕円平面状の物体(例えば,腕)に対するホモグラフィ行列を求めます.
パラメタ: - line – 物体の主軸方向(ベクトル(dx,dy,dz).
- center – 物体中心(cx,cy,cz).
- intrinsic – カメラの内部パラメータ(3x3 の行列).
- homography – 出力されるホモグラフィ行列(3x3).
この関数は,3次元楕円体の主軸で定義されるような,画像平面から平面への変換を行うホモグラフィ行列を求めます (OpenCV Guide の 3D Reconstruction の章にある図6-10を参照してください).
CalibrateCamera2¶
- double cvCalibrateCamera2(const CvMat* objectPoints, const CvMat* imagePoints, const CvMat* pointCounts, CvSize imageSize, CvMat* cameraMatrix, CvMat* distCoeffs, CvMat* rvecs=NULL, CvMat* tvecs=NULL, int flags=0)¶
キャリブレーションパターンを写した複数のビューから,カメラの内部・外部パラメータを求めます.
パラメタ: - objectPoints – 物体上の点群,つまりモデル座標空間におけるキャリブレーションパターンの特徴点座標,の結合行列.これは浮動小数点型で, 3xN または Nx3 の1チャンネル,あるいは 1xN または Nx1 の3チャンネル配列です.ここで N は全てのビューにおける点の総数を表します.
- imagePoints – 物体上の点群をカメラビューに投影した点群の結合行列.これは浮動小数点型で,2xN または Nx2 の1チャンネル,あるいは 1xN または Nx1 の2チャンネル配列です.ここで N は全てのビューにおける点の総数を表します.
- pointCounts – 各ビューにおける点の個数を表す,1xM または Mx1 の整数型ベクトル(ここで M はキャリブレーションパターンのビューの数を表します).ベクトル要素の合計値は, objectPoints および imagePoints (=N) と一致しなければいけません.
- imageSize – 画像サイズ.カメラの内部行列を初期化するためだけに利用されます.
- cameraMatrix – 入出力用の,カメラの内部パラメータ行列
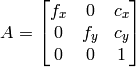 . CV_CALIB_USE_INTRINSIC_GUESS および/または CV_CALIB_FIX_ASPECT_RATIO が指定される場合, fx, fy, cx, cy のいくつか,あるいはすべてが初期化されていなければなりません.
. CV_CALIB_USE_INTRINSIC_GUESS および/または CV_CALIB_FIX_ASPECT_RATIO が指定される場合, fx, fy, cx, cy のいくつか,あるいはすべてが初期化されていなければなりません. - distCoeffs – 歪み係数の出力ベクトル
![(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6]])](_images/math/7c67b59b59778bc682b2d972bde3d910b2326924.png) .4,5,または8要素となります.
.4,5,または8要素となります. - rvecs – 出力される 3x M または M x3 のシングルチャンネル,あるいは 1x M または M x1 の3チャンネル配列 .各ビューにおいて推定された回転ベクトルを表します( Rodrigues2 を参照してください).つまり,k番目の回転ベクトルとk番目の並進ベクトル(下の出力パラメータの説明を参照してください)によって,キャリブレーションパターンが,モデル座標空間(物体上の点が指定される空間)からワールド座標空間,つまり,k番目のビューにおけるキャリブレーションパターンの実際の位置に移動することになります(k=0.. M -1).
- tvecs – 出力される 3x M または M x3 でシングルチャンネル,あるいは 1x M または M x1 で3チャンネルの配列 .各ビューにおいて推定された並進ベクトルを表します.
- flags –
様々なフラグ.0,あるいは以下の値の組み合わせ:
- CV_CALIB_USE_INTRINSIC_GUESS cameraMatrix が fx, fy, cx, cy の有効な初期値を含み,これらが最適化されます.そうでない場合は, (cx, cy) には初期値として画像中心(これは入力の imageSize から求められます)がセットされ,焦点距離は最小二乗法で計算されます.もし内部パラメータが既知ならば,外部パラメータを推定するためだけにこの関数を使う必要はないことに注意してください.代わりに FindExtrinsicCameraParams2 を利用しましょう.
- CV_CALIB_FIX_PRINCIPAL_POINT 大域的最適化中に,主点が変更されません.主点は画像中心か,あるいは CV_CALIB_USE_INTRINSIC_GUESS が同時にセットされている場合は,別のの指定位置にとどまります.
- CV_CALIB_FIX_ASPECT_RATIO この関数は fy だけを自由パラメータとみなして,入力の cameraMatrix で指定された比率 fx/fy を保ちます. CV_CALIB_USE_INTRINSIC_GUESS がセットされていない場合, fx と fy の実際の入力値は無視され,その比率だけが計算されて利用されます.
- CV_CALIB_ZERO_TANGENT_DIST 円周方向の歪み係数
 が0にセットされ,そのまま変更されません
が0にセットされ,そのまま変更されません
.- CV_CALIB_FIX_K1,...,CV_CALIB_FIX_K6 最適化中に,指定した半径方向の歪み係数を変更しません. CV_CALIB_USE_INTRINSIC_GUESS が指定されている場合は,与えられた distCoeffs 行列の係数が利用されます.そうでない場合は,0が利用されます.
- CV_CALIB_RATIONAL_MODEL 係数 k4, k5, k6 を有効にします.後方互換性を保つためには,このフラグを明示的に指定して,キャリブレーション関数が rational モデルを利用して8個の係数を返すようにします.このフラグが指定されない場合,関数は5つの歪み係数のみを計算し ます.
この関数は,カメラの内部パラメータ,および各ビューにおける外部パラメータを推定します.各画像における,3次元点の座標と,それに対応する2次元の投影点の座標を指定する必要があります.これは,幾何的な特徴が既知で,容易に特徴点を検出できるような物体を用いて行われます. そのような物体は,キャリブレーション器具またはキャリブレーションパターンと呼ばれます.OpenCVは元々,キャリブレーション器具としてチェスボードをサポートしています( FindChessboardCorners を参照してください).現在のところ,内部パラメータの初期化は,(物体上の点群のz-座標がすべて0になる)平面キャリブレーションパターンに対してのみ実装されています( CV_CALIB_USE_INTRINSIC_GUESS がセットされない場合).初期 cameraMatrix が与えられれば,3次元のキャリブレーション器具も利用することができます.
このアルゴリズムは,次のようになります:
- まず,内部パラメータの初期値を,計算する(これは,平面キャリブレーションパターンを利用した場合のみ可能)か,あるいは入力パラメータから読み込みます.歪み係数は,( CV_CALIB_FIX_K? で指定されているものを除いて)すべて0にセットされます.
- 内部パラメータが既知であるかのように,カメラの初期姿勢を推定します.この推定には, FindExtrinsicCameraParams2 を利用します.
- 再投影誤差を最小にするように,大域的な Levenberg-Marquardt 最適化アルゴリズムが実行されます.つまり,観測された特徴点 imagePoints と,(内部パラメータとカメラ姿勢の現在の推定値を利用した)投影点 objectPoints との距離の2乗和を最小にします. ProjectPoints2 を参照してください.
この関数は,最終的な再投影誤差を返します.
注意:正方ではない(NxN ではない)グリッドを使用して,
findChessboardCorners()
でキャリブレーションを行う場合に,
calibrateCamera
が不正な値(つまり,歪み係数が0,画像中心が
 から遠く離れている,さらに/または,
から遠く離れている,さらに/または,
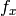 と
と
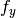 が大きく異なる(比率が 10:1 以上))を返すとすると,
FindChessboardCorners
で
patternSize=cvSize(rows,cols)
としている可能性があります.正しくは,
patternSize=cvSize(cols,rows)
となります.
が大きく異なる(比率が 10:1 以上))を返すとすると,
FindChessboardCorners
で
patternSize=cvSize(rows,cols)
としている可能性があります.正しくは,
patternSize=cvSize(cols,rows)
となります.
参考: FindChessboardCorners , FindExtrinsicCameraParams2 , initCameraMatrix2D() , StereoCalibrate , Undistort2
ComputeCorrespondEpilines¶
- void cvComputeCorrespondEpilines(const CvMat* points, int whichImage, const CvMat* F, CvMat* lines)¶
ステレオペアの片方の画像上の点に対して,それに対応する別の画像上のエピポーラ線を求めます.
パラメタ: - points – 入力点. 2xN, Nx2, 3xN または Nx3 の配列(ここで N は点の個数です).マルチチャンネルの 1xN または Nx1 配列も同様に渡すことができます.
- whichImage – points を含む画像のインデックス(1または2).
- F – FindFundamentalMat または StereoRectify によって指定されるF行列.
- lines – 出力されるエピポーラ線. 3xN または Nx3 の配列. 各エピポーラ線
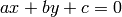 は,3つの数値
は,3つの数値 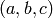 で符号化されます.
で符号化されます.
この関数は,ステレオペアの2つの画像の片方に存在する点それぞれに対して,対応する別の画像上のエピポーラ線を求めます.
F行列の定義から(
FindFundamentalMat
を参照してください),1番目の画像(つまり,
whichImage=1
)上の点
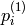 に対する,2番目の画像上の線
に対する,2番目の画像上の線
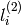 は次のように求められます:
は次のように求められます:
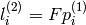
そして,逆に
whichImage=2
の場合,
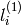 は,
は,
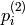 から,次のように求められます:
から,次のように求められます:
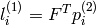
エピポーラ線の係数には,スケールが定義されています.これらは
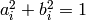 というように正規化されます.
というように正規化されます.
ConvertPointsHomogeneous¶
- void cvConvertPointsHomogeneous(const CvMat* src, CvMat* dst)¶
点座標と同次座標を,互いに変換します.
パラメタ: - src – 入力点の配列. 2xN, Nx2, 3xN, Nx3, 4xN または Nx4(ここで ``N は,点の個数を表します)`` .マルチチャンネルで 1xN または Nx1 の配列も同様に渡すことができます.
- dst – 出力点の配列.必ず入力と同じ数の点を含んでいます.次元数は同じ入力と同じ,1つ小さい,または1つ大きいのいずれかで,2から4の間の数となります.
この関数は, 2次元または3次元の点と,同次座標を相互に変換,あるいは単に コピーや転置 を行います.入力配列の次元数が出力よりも大きい場合は,各座標値が最後の座標値で割られます:
![\begin{array}{l} (x,y[,z],w) -> (x',y'[,z']) \\ \text{where} \\ x' = x/w \\ y' = y/w \\ z' = z/w \quad \text{(if output is 3D)} \end{array}](_images/math/8da5c69bcb6b6386781ae5cdcd555ed70460e785.png)
出力配列の次元数の方が大きい場合は,各入力点に値1が付け加えられます.それ以外の場合は単に,入力配列が出力配列にコピーされます(転置することもできます).
注意 :この関数は様々な形式の配列を入力にとるので,入出力配列の次元があいまいな場合はエラーが起こる可能性があります. 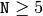 個の点,あるいは,マルチチャンネルで Nx1 または 1xN の配列,に対して利用する場合は,常に安全です.
個の点,あるいは,マルチチャンネルで Nx1 または 1xN の配列,に対して利用する場合は,常に安全です.
CreatePOSITObject¶
- CvPOSITObject* cvCreatePOSITObject(CvPoint3D32f* points, int point_count)¶
物体情報を含む構造体を初期化します.
パラメタ: - points – 3次元物体モデルの点座標へのポインタ.
- point_count – 物体点座標の個数.
この関数は,物体情報構造体のメモリを確保し,物体逆行列を計算します.
事前に処理された物体データは,OpenCV 内部で構造体 CvPOSITObject に格納されるので,ユーザが構造体データに直接アクセスすることはできません.つまり,ユーザはこの構造体を作成し,そのポインタをこの関数に渡すだけです.
物体は,ある座標系の点座標の集合として定義されます.そして,関数 POSIT は,カメラ座標系の中心から,物体の points[0] へのベクトルを計算します.
与えられた物体に対する処理が終わった後は,関数 ReleasePOSITObject を呼んでメモリを解放しなければいけません.
CreateStereoBMState¶
- CvStereoBMState* cvCreateStereoBMState(int preset=CV_STEREO_BM_BASIC, int numberOfDisparities=0)¶
ブロックマッチングステレオ対応点探索の構造体を作成します.
パラメタ: - preset –
あらかじめ定義されたパラメータセットのID.どのパラメータも,この構造体を作成した後に上書きすることができます.この値は次のようになります.
- CV_STEREO_BM_BASIC 一般的なカメラに適合するパラメータ
- CV_STEREO_BM_FISH_EYE 広角カメラに適合するパラメータ
- CV_STEREO_BM_NARROW 狭角カメラに適合するパラメータ
- numberOfDisparities – 視差数.このパラメータが0の場合,preset から取得した値を利用します.そうでない場合,この値が preset の値を上書きします.
- preset –
この関数は,ステレオ対応点探索の構造体を作成し,それを初期化します.また, FindStereoCorrespondenceBM 呼び出しまでの間ならばいつでも,すべてのパラメータを上書きすることが可能です.
CreateStereoGCState¶
- CvStereoGCState* cvCreateStereoGCState(int numberOfDisparities, int maxIters)¶
グラフカットに基づくステレオ対応点探索アルゴリズムの構造体を作成します.
パラメタ: - numberOfDisparities – 視差数.視差の探索範囲は
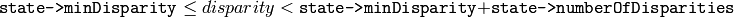 となります.
となります. - maxIters – 反復処理の最大数.各試行で,取り得るすべての(あるいは,適度な数の)α拡張を行います.このアルゴリズムは,コスト関数全体を減少させるα拡張が見つからなかった場合は,そこで終了します.詳しくは, Kolmogorov03 を参照してください.
- numberOfDisparities – 視差数.視差の探索範囲は
この関数は,ステレオ対応点探索の構造体を作成し,それを初期化します.また, FindStereoCorrespondenceGC 呼び出しまでの間ならばいつでも,すべてのパラメータを上書きすることが可能です.
CvStereoBMState¶
- CvStereoBMState¶
ブロックマッチングステレオ対応点探索アルゴリズムのための構造体.
typedef struct CvStereoBMState
{
// 事前フィルタ(入力画像を正規化します):
int preFilterType; // 現在は 0
int preFilterSize; // 約 5x5..21x21
int preFilterCap; // 約 31 までの値
// 絶対値の差の合計(SAD)を用いて対応点探索を行います:
int SADWindowSize; // おそらく 5x5..21x21
int minDisparity; // 最小視差 (=0)
int numberOfDisparities; // 最大視差 - 最小視差
// 事後フィルタ(不良なマッチを除外します):
int textureThreshold; // テクスチャがない領域を無視します.
int uniquenessRatio; // 別の視差でもステレオ対応するようなピクセルを,
// 視差が無効なものとします.
int speckleWindowSize; // 除去されるスペックルの最大面積
// ( 0 にするとスペックルフィルタリングは無効になります)
int speckleRange; // 各連結成分において,許容される視差範囲
int trySmallerWindows; // 利用されません
CvRect roi1, roi2; // クリッピングするための ROI
int disp12MaxDiff; // left-right チェックを行う際の,最大許容視差
// 内部データ
...
}
CvStereoBMState;
- preFilterType¶
事前フィルタの種類. CV_STEREO_BM_NORMALIZED_RESPONSE あるいは,デフォルトかつ推奨値である CV_STEREO_BM_XSOBEL のどちらか, int型.
- preFilterSize¶
5x5..21x21,int型.
- preFilterCap¶
31 までの値,int型.
- SADWindowSize¶
5x5..21x21 あるいは,それ以上の値.ただし,21x21 以下のサイズの窓であれば,処理がかなり高速です,int型.
- minDisparity¶
最小視差 (=0),int型.
- numberOfDisparities¶
最大視差 - 最小視差,int型.
- textureThreshold¶
テクスチャ閾値.つまり, SADWindowSize × SADWindowSize の近傍で求められた x-微分の絶対値の総和がこのパラメータよりも小さければ,その対象ピクセルでは視差が計算されません,int型.
- uniquenessRatio¶
求められた視差が有功になるための,最良(最小)のコスト関数値と2番目に良い値との最小マージン(パーセント単位).
- speckleWindowSize¶
除去されるスペックルの最大面積( 0 にするとスペックルフィルタリングは無効になります),int型.
- speckleRange¶
各連結成分において,許容される視差範囲,int型.
- trySmallerWindows¶
現在は利用されていません(0),int型.
- roi1, roi2
左右の画像をクリッピングするためのROI.関数 StereoRectify は,左右の画像の最大の矩形を返します.また,この平行化変換後もすべてのピクセルが有効になります.これらの矩形を CvStereoBMState 構造体にコピーすると,ステレオ対応点探索関数は自動的に, GetValidDisparityROI によって求められた「有効な」視差矩形の外側のピクセルをクリアします.よって,通常よりも「無効な視差」ピクセルが多くなりますが,残ったピクセルは,有効である可能性がより高いものになります.
- disp12MaxDiff¶
明示的に求められた左から右への視差マップと,黙示的に( ValidateDisparity によって)求められた右から左への視差マップとの間の,許容される最大の差.この差が指定の閾値よりも大きいピクセルでの視差は無効になります.デフォルトでは,このパラメータは(-1)にセットされており,これは left-right チェックが行われないことを意味します.
Kurt Konolige によるブロックマッチングによるステレオ対応点探索アルゴリズムは,非常に高速なシングルパスのステレオマッチングアルゴリズムです.これは,左右の画像において比較するピクセル位置のずれを(
minDisparity
から
minDisparity+numberOfDisparities
まで)変化させながら,輝度値の差の絶対値の総和を画像全体に渡って計算します.このアルゴリズムは,
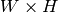 の画像のペアにおいて,その視差を
O(W*H*numberOfDisparities)
回計算します.また,このアルゴリズムは,視差画像の質と信頼性を向上させるために,事前フィルタおよび事後フィルタを導入しています.
の画像のペアにおいて,その視差を
O(W*H*numberOfDisparities)
回計算します.また,このアルゴリズムは,視差画像の質と信頼性を向上させるために,事前フィルタおよび事後フィルタを導入しています.
このアルゴリズムは,対応するブロックを,x-軸方向にのみ探索する事に注意してください.つまり,この関数の適用対象となるのは,平行化されたステレオペアです.また,垂直ステレオは直接はサポートされていませんが,そのような場合,ユーザは画像を転置させればよいでしょう.
CvStereoGCState¶
- CvStereoGCState¶
グラフカットに基づく,ステレオ対応点探索アルゴリズムのための構造体.
typedef struct CvStereoGCState
{
int Ithreshold; // データ項の閾値(デフォルトでは 5 )
int interactionRadius; // 平滑化項の範囲(デフォルトでは 1 ,つまり Potts モデル)
float K, lambda, lambda1, lambda2; // コスト関数のパラメータ
// (通常は,入力データから適応的に求められます)
int occlusionCost; // デフォルトでは 10000
int minDisparity; // デフォルトでは 0 .CvStereoBMState を参照してください
int numberOfDisparities; // ユーザが定義します. CvStereoBMState を参照してください
int maxIters; // 反復計算回数.ユーザが定義します.
// internal buffers
CvMat* left;
CvMat* right;
CvMat* dispLeft;
CvMat* dispRight;
CvMat* ptrLeft;
CvMat* ptrRight;
CvMat* vtxBuf;
CvMat* edgeBuf;
}
CvStereoGCState;
Kolmogrov03 で( KZ1 として)紹介されたグラフカットステレオ対応点探索アルゴリズムは,非リアルタイムのステレオマッチングアルゴリズムであり,通常,明確なオブジェクト境界を示す非常に正確な奥行き画像を求めます.このアルゴリズムは,ステレオ問題を2値最適化問題のシーケンスとして扱い,それぞれを最大流アルゴリズム(max flow algorithm)を用いて解きます.上述の構造体は,手動で確保,初期化されるべきではりません.その代わりに, cvCreateStereoGCState を利用し,必要ならばパラメータを上書きしてください.
DecomposeProjectionMatrix¶
- void cvDecomposeProjectionMatrix(const CvMat *projMatrix, CvMat *cameraMatrix, CvMat *rotMatrix, CvMat *transVect, CvMat *rotMatrX=NULL, CvMat *rotMatrY=NULL, CvMat *rotMatrZ=NULL, CvPoint3D64f *eulerAngles=NULL)¶
射影行列を,回転行列とカメラ行列に分解します.
パラメタ: - ProjMatrix – 3x4 の入力射影行列 P .
- cameraMatrix – 3x3 の出力カメラ行列 K .
- rotMatrix – 3x3 の出力回転行列 R .
- transVect – 4x1 の出力並進ベクトル T .
- rotMatrX – オプション.3x3 の x-軸周りの回転行列.
- rotMatrY – オプション.3x3 の y-軸周りの回転行列.
- rotMatrZ – オプション.3x3 の z-軸周りの回転行列.
- eulerAngles – オプション.回転を表す3つのオイラー角.
この関数は,射影行列をカメラ行列と回転行列,カメラの位置に分解します.
またオプションとして,各軸周りの3つの回転行列,そして OpenGL で利用できる3つのオイラー角を得ることができます.
この関数は, RQDecomp3x3 に基づいています.
DrawChessboardCorners¶
- void cvDrawChessboardCorners(CvArr* image, CvSize patternSize, CvPoint2D32f* corners, int count, int patternWasFound)¶
検出されたチェスボードのコーナーを描画します.
パラメタ: - image – 出力画像.8ビットのカラー画像.
- patternSize – チェスボード内の,行と列毎の内側コーナー数.(patternSize = cv::Size(points _ per _ row,points _ per _ column) = cv::Size(columns,rows) ) .
- corners – 検出されたコーナーの配列.これは findChessboardCorners の出力を cv::Mat() でラップしたものです.
- count – コーナーの個数.
- patternWasFound – チェスボードが完全に検出された
 か,否
か,否  かを示します.ここでは単に FindChessboardCorners の戻り値を渡すことができます.
かを示します.ここでは単に FindChessboardCorners の戻り値を渡すことができます.
この関数は,検出された個々のチェスボードを描画します.チェスボードが不完全に検出された場合は,検出されたコーナーが赤い丸で描画され,完全に検出された場合は,色付きのコーナーが線で結ばれます.
FindChessboardCorners¶
- int cvFindChessboardCorners(const void* image, CvSize patternSize, CvPoint2D32f* corners, int* cornerCount=NULL, int flags=CV_CALIB_CB_ADAPTIVE_THRESH)¶
チェスボードの内側コーナー位置を求めます.
パラメタ: - image – チェスボードのビュー.8ビットグレースケール画像,またはカラー画像でなければいけません.
- patternSize – チェスボードの行と列毎の,内側コーナーの個数( patternSize = cvSize(points _ per _ row,points _ per _ colum) = cvSize(columns,rows) ) .
- corners – 検出されたコーナーの出力配列.
- cornerCount – 出力コーナーカウンタ.これがNULLでなければ,ここに検出されたコーナーの個数が格納されます.
- flags –
様々な処理フラグ.0または以下の値の組み合わせです:
- CV_CALIB_CB_ADAPTIVE_THRESH 入力画像を白黒画像に変換する際に,(画像の明るさの平均値から計算された)固定閾値の代わりに適応的閾値を利用します.
- CV_CALIB_CB_NORMALIZE_IMAGE 固定あるいは適応的閾値を適用する前に, EqualizeHist を用いて画像のガンマ値を正規化します.
- CV_CALIB_CB_FILTER_QUADS 輪郭抽出の際に検出された誤った四角を除外するために,(輪郭領域面積,周囲長,正方形度合い,のような)追加の基準を利用します.
- CALIB_CB_FAST_CHECK 画像からチェスボードのコーナーを探す高速なチェックを行い,もし見つからなければ関数呼び出しをショートカットします.これによって,劣悪な条件下でチェスボードが観測できない場合に,この呼び出しを非常に高速化することができます.
この関数は,入力画像がチェスボードパターンを写すビューであるかどうかを判断し,もしそうならば,チェスボードの内側コーナーの位置を検出しようとします.これは,すべてのチェスボードコーナーが検出された場合は真値を返し,そのコーナーは特定の順序(1行ごとに,各行は左から右に)で格納されます.そうでない場合,つまり,コーナーの完全な検出や順序づけに失敗した場合は,0を返します.例えば,標準的なチェスボードは, 8 x 8 マスで 7 x 7 個の内側コーナー,つまり黒い正方形が別の黒い正方形と接触する点,をもちます.検出される座標は近似されたもので,より正確な位置を決定するために,関数 FindCornerSubPix を利用する場合があります.
チェスボードのコーナー検出と描画方法のサンプル:
Size patternsize(8,6); // 内部にあるコーナーの個数
Mat gray = ....; // 入力画像
vector<Point2f> corners; // 検出されたコーナーがここに入ります
// CALIB_CB_FAST_CHECK を使うと,画像中にチェスボードコーナーが
// 無かった場合に,時間を大幅に節約できます
bool patternfound = findChessboardCorners(gray, patternsize, corners,
CALIB_CB_ADAPTIVE_THRESH + CALIB_CB_NORMALIZE_IMAGE
+ CALIB_CB_FAST_CHECK);
if(patternfound)
cornerSubPix(gray, corners, Size(11, 11), Size(-1, -1),
TermCriteria(CV_TERMCRIT_EPS + CV_TERMCRIT_ITER, 30, 0.1));
drawChessboardCorners(img, patternsize, Mat(corners), patternfound);
注意: この関数では,様々な環境下でロバストな検出を行うために,チェスボードの周囲に(太い枠淵のような,広ければ広いほど良い)空白が必要です(もし,この空白がなく背景が暗ければ,外側の黒い正方形が適切に分離されず,正方形のグループ分けと順序付けアルゴリズムは失敗するでしょう).
FindExtrinsicCameraParams2¶
- void cvFindExtrinsicCameraParams2(const CvMat* objectPoints, const CvMat* imagePoints, const CvMat* cameraMatrix, const CvMat* distCoeffs, CvMat* rvec, CvMat* tvec, int useExtrinsicGuess=0)¶
3次元-2次元の対応点から,物体の姿勢を求めます.
パラメタ: - objectPoints – 物体座標空間における物体上の点座標の配列.3xN または Nx3 のシングルチャンネル配列,あるいは 1xN または Nx1 の3チャンネル配列.ここで N は点の個数を表します.
- imagePoints – 画像上の対応点の配列.2xN または Nx2 のシングルチャンネル配列,あるいは 1xN または Nx1 の2チャンネル配列.ここで N は点の個数を表します.
- cameraMatrix – 入力されるカメラ行列
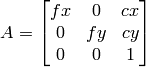
- distCoeffs – 入力される歪み係数ベクトル
![(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6]])](_images/math/7c67b59b59778bc682b2d972bde3d910b2326924.png) .4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます.
.4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます. - rvec – 出力される回転ベクトル( Rodrigues2 を参照してください).( tvec とともに用いることで)座標点をモデル座標系からカメラ座標系に変換します.
- tvec – 出力される並進ベクトル.
- useExtrinsicGuess – これが true (1) の場合,この関数は,与えられた rvec と tvec を,それぞれ回転ベクトルと並進ベクトルの初期近似値として利用し,それらを最適化します.
この関数は,カメラ行列や歪み係数と共に,物体上の点座標とそれに対応する画像上の投影点の集合が与えられた場合に,物体の姿勢を推定します.そのような姿勢は,再投影誤差を最小にするように求められます.つまり,観測された投影点 imagePoints と( ProjectPoints2 を用いて) objectPoints を投影した点との距離の二乗和を最小にします.
この関数に対応する C++ API は cv::solvePnP です.
FindFundamentalMat¶
- int cvFindFundamentalMat(const CvMat* points1, const CvMat* points2, CvMat* fundamentalMatrix, int method=CV_FM_RANSAC, double param1=1., double param2=0.99, CvMat* status=NULL)¶
2つの画像の対応点からF行列を求めます.
パラメタ: - points1 – 1番目の画像中の N 個の点の配列. 2xN, Nx2, 3xN または Nx3 のシングルチャンネル配列,あるいは 1xN または Nx1 の2チャンネル,3チャンネル配列 .点座標は,浮動小数点型(単精度または倍精度)です.
- points2 – 2番目の画像中対応点の配列. points1 と同じサイズ,同じフォーマット.
- fundamentalMatrix – 出力されるF行列.サイズは 3x3 または 9x3 (7-point アルゴリズムは3つまでの行列を返します).
- method –
F行列を計算する手法
- CV_FM_7POINT 7-point アルゴリズム.
- CV_FM_8POINT 8-point アルゴリズム.
- CV_FM_RANSAC RANSAC アルゴリズム.
- CV_FM_LMEDS LMedS アルゴリズム.
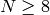
- CV_FM_7POINT 7-point アルゴリズム.
- param1 – RANSAC の場合のみ利用されるパラメータ.点からエピポーラ線までの最大距離をピクセル単位で表します.その距離を超えるものは外れ値であると判断され,最終的なF行列の計算に使用されません.点座標の精度,画像の解像度,画像のノイズなどに依存して,1-3程度の値にセットされます.
- param2 – RANSAC または LMedS の場合にのみ使用されるパラメータ.推定されるF行列がどれほど正しいかを示す信頼(確率)値の要求値を表します.
- status – オプション. N要素の出力配列.各要素は対応する点が外れ値ならば0にセットされ,そうでなければ1にセットされます.この配列は, RANSAC または LMedS の場合のみ計算されます.その他の手法の場合は,すべて1にセットされます.
エピポーラ幾何は,次の式で説明されます:
![[p_2; 1]^T F [p_1; 1] = 0](_images/math/0ba9438e14e73a4bac80f18d7aa26cb1c2531543.png)
ここで,
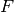 はF行列,
はF行列,
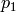 と
と
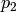 はそれぞれ,1番目と2番目の画像での対応点を表します.
はそれぞれ,1番目と2番目の画像での対応点を表します.
この関数は,上述の4つの手法の内の1つを用いてF行列を計算し,
求められたF行列の個数(1または3)を返し,求まらなかった場合は0
を返します.
通常,行列は1つだけ求められますが,7-point アルゴリズムを利用する場合,この関数は3つまでの解(すべての行列を順番に格納した
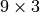 の行列)を返すことがあります.
の行列)を返すことがあります.
計算されたF行列はさらに,指定された点に対応するエピポーラ線を求める関数 ComputeCorrespondEpilines に渡される場合があります.また,平行化変換を求めるために StereoRectifyUncalibrated に渡すこともできます.
int point_count = 100;
CvMat* points1;
CvMat* points2;
CvMat* status;
CvMat* fundamental_matrix;
points1 = cvCreateMat(1,point_count,CV_32FC2);
points2 = cvCreateMat(1,point_count,CV_32FC2);
status = cvCreateMat(1,point_count,CV_8UC1);
/* ここで点座標を埋めます ... */
for( i = 0; i < point_count; i++ )
{
points1->data.fl[i*2] = <x,,1,i,,>;
points1->data.fl[i*2+1] = <y,,1,i,,>;
points2->data.fl[i*2] = <x,,2,i,,>;
points2->data.fl[i*2+1] = <y,,2,i,,>;
}
fundamental_matrix = cvCreateMat(3,3,CV_32FC1);
int fm_count = cvFindFundamentalMat( points1,points2,fundamental_matrix,
CV_FM_RANSAC,1.0,0.99,status );
FindHomography¶
- void cvFindHomography(const CvMat* srcPoints, const CvMat* dstPoints, CvMat* H int method=0, double ransacReprojThreshold=3, CvMat* status=NULL)¶
2つの画像間の透視変換を求めます.
パラメタ: - srcPoints – 元平面の点群の座標.2xN, Nx2, 3xN または Nx3 のシングルチャンネル配列(後者2つは同次座標系における表現).ここで N は点の個数を表します.1xN または Nx1 の2チャンネル配列,3チャンネル配列も同様に渡すことができます.
- dstPoints – 目的平面の点群の座標.2xN, Nx2, 3xN または Nx3 のシングルチャンネル配列,あるいは 1xN または Nx1 の2チャンネル配列,3チャンネル配列.
- H – 出力される 3x3 のホモグラフィ行列.
- method –
ホモグラフィ行列を求めるための手法:以下の内の1つ:
- 0 点の組をすべて利用する通常の手法
- CV_RANSAC RANSACアルゴリズムに基づくロバストな手法
- CV_LMEDS LMedS推定(Least-Median)によるロバストな手法
- ransacReprojThreshold –
点の組を,インライア値(外れ値ではないもの)として扱うために許容される逆投影誤差の最大値(これは,RANSACメソッドでのみ利用されます).つまり,もし
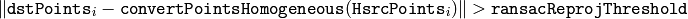
であれば,点
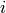 は外れ値であるとみなされます. srcPoints と dstPoints がピクセル単位で表されているならば,このパラメータは1から10の範囲内の値が妥当です.
は外れ値であるとみなされます. srcPoints と dstPoints がピクセル単位で表されているならば,このパラメータは1から10の範囲内の値が妥当です. - status – ロバスト手法( CV_RANSAC または CV_LMEDS )を利用した場合に,オプションとして出力されるマスク. 入力マスク値は無視されることに注意してください.
この関数
は,元平面と目的平面との間の透視変換
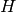 を求め
ます:
を求め
ます:
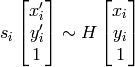
つまり,以下の逆投影誤差を最小化します.
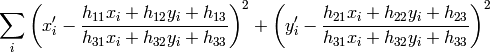
パラメータ method がデフォルト値の 0 にセットされた場合,この関数はすべての点の組を利用して,単純な最小二乗法によりホモグラフィ行列を推定します.
しかし,透視投影変換ですべての点の組(
 ,
,
 )を一致させることができない(つまり,外れ値がある)場合でも,ロバストな手法を選択することで正しい変換を推定することができます.
RANSAC
と
LMedS
のどちらの手法も,対応する点の組のランダムな部分集合(各4組)を繰り返し生成し,この部分集合と単純な最小二乗法を用いてホモグラフィ行列を推定します.そして,求められたホモグラフィ行列の質/状態(RANSACの場合はインライアの数,LMedS推定の場合は中央値の逆投影誤差)を計算します.
この最適な部分集合から,ホモグラフィ行列の初期推定値とインライア/アウトライアのマスクが生成されます.
)を一致させることができない(つまり,外れ値がある)場合でも,ロバストな手法を選択することで正しい変換を推定することができます.
RANSAC
と
LMedS
のどちらの手法も,対応する点の組のランダムな部分集合(各4組)を繰り返し生成し,この部分集合と単純な最小二乗法を用いてホモグラフィ行列を推定します.そして,求められたホモグラフィ行列の質/状態(RANSACの場合はインライアの数,LMedS推定の場合は中央値の逆投影誤差)を計算します.
この最適な部分集合から,ホモグラフィ行列の初期推定値とインライア/アウトライアのマスクが生成されます.
手法がロバストかどうかにかかわらず,求められたホモグラフィ行列は,逆投影誤差がより小さくなるように,Levenberg-Marquardt 法を用いてさらに(ロバスト推定の場合はインライア値のみを利用して)高精度化されます.
RANSAC を指定すると,実際にはどれだけアウトライアが混ざったデータも扱うことができますが,インライアとアウトライアを区別するための閾値が必要となります. LMedS を指定すると,この様な閾値は必要なくなりますが,データの50 % 以上がインライアでなければ正しく動作しません. また,計算された特徴点列内存在するノイズが僅かであり,アウトライアがないことが分かっている場合は,デフォルトの手法が最も良い選択です.
この関数は,内部および外部パラメータ行列の初期推定値を求めるために利用されます.
ホモグラフィ行列は,スケールに依存するので,
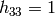 となるように正規化されます.
となるように正規化されます.
参考: GetAffineTransform , GetPerspectiveTransform , EstimateRigidMotion , WarpPerspective , PerspectiveTransform
FindStereoCorrespondenceBM¶
- void cvFindStereoCorrespondenceBM(const CvArr* left, const CvArr* right, CvArr* disparity, CvStereoBMState* state)¶
ブロックマッチングアルゴリズムを用いて視差画像を求めます.
パラメタ: - left – シングルチャンネル,8ビットの左画像.
- right – 左画像と同じサイズ,同じ型の右画像.
- disparity – 出力視差マップ.シングルチャンネル,16ビット符号あり整数型,または32ビット浮動小数点型で,入力画像と同じサイズのマップです.前者の場合,計算される視差は小数点以下が4ビットの固定小数点数として表現されます(つまり,求められる視差値が16倍され,整数へと丸められたものです).
- state – ステレオ対応点探索構造体.
この関数は,入力された平行化されたステレオ画像ペアに対する視差マップを計算します.(視差が計算できないような)無効なピクセルの値は state->minDisparity - 1 (16ビット固定小数点視差マップの場合は, (state->minDisparity-1)*16 )にセットされます.
FindStereoCorrespondenceGC¶
- void cvFindStereoCorrespondenceGC(const CvArr* left, const CvArr* right, CvArr* dispLeft, CvArr* dispRight, CvStereoGCState* state, int useDisparityGuess = CV_DEFAULT(0))¶
グラフカットアルゴリズムを用いて視差マップを求めます.
パラメタ: - left – シングルチャンネル,8ビットの左画像.
- right – 左画像と同じサイズ,同じ型の右画像.
- dispLeft – 出力オプション.シングルチャンネル,16ビット,符号あり整数.入力画像と同じサイズの左視差画像.
- dispRight – 出力オプション.シングルチャンネル,16ビット,符号あり整数.入力画像と同じサイズの右視差画像.
- state – ステレオ対応点探索構造体.
- useDisparityGuess – このパラメータが 0 でない場合,あらかじめ定義された視差マップを利用して計算が開始されます.つまり,dispLeft と dispRight が共に,妥当な視差画像である必要があります.そうでない場合,(すべてのピクセルがオクルージョンとなっている)空の視差マップから開始されます.
この関数は,平行化された入力ステレオ画像ペアに対する視差マップを計算します.左視差画像は,次の範囲の値を含むことに注意してください:
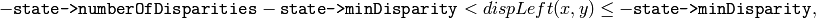
または
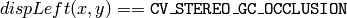
そして,右視差画像は,次の範囲の値を含みます:
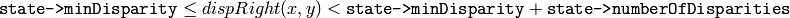
または
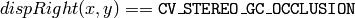
つまり,右視差画像と左視差画像では範囲が逆になっています.そして,マッチング結果がよくないピクセルは,オクルージョンとして処理されます.
以下は,この関数の使用例です:
// image_left と image_right はそれぞれ,
// 左右のカメラの 8 ビット,シングルチャンネルの入力画像です
CvSize size = cvGetSize(image_left);
CvMat* disparity_left = cvCreateMat( size.height, size.width, CV_16S );
CvMat* disparity_right = cvCreateMat( size.height, size.width, CV_16S );
CvStereoGCState* state = cvCreateStereoGCState( 16, 2 );
cvFindStereoCorrespondenceGC( image_left, image_right,
disparity_left, disparity_right, state, 0 );
cvReleaseStereoGCState( &state );
// 計算された視差画像を使って,以下で好きな処理を行います ...
以下は,有名な Tsukuba ステレオ画像ペアから計算された出力左視差画像を,-16 倍したものです(通常,左視差画像は負の値を持つので):
CvMat* disparity_left_visual = cvCreateMat( size.height, size.width, CV_8U );
cvConvertScale( disparity_left, disparity_left_visual, -16 );
cvSave( "disparity.pgm", disparity_left_visual );

GetOptimalNewCameraMatrix¶
- void cvGetOptimalNewCameraMatrix(const CvMat* cameraMatrix, const CvMat* distCoeffs, CvSize imageSize, double alpha, CvMat* newCameraMatrix, CvSize newImageSize=cvSize(0, 0), CvRect* validPixROI=0)¶
フリースケーリングパラメータに基づいて,新たなカメラ行列を返します.
パラメタ: - cameraMatrix – 入力されるカメラ行列.
- distCoeffs – 入力される歪み係数ベクトル
![(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6]])](_images/math/7c67b59b59778bc682b2d972bde3d910b2326924.png) .4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます.
.4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます. - imageSize – 最適画像サイズ.
- alpha – フリースケーリングパラメータ.0(歪み補正後の画像の全ピクセルが有効になるように切り抜き)から1(歪み補正された画像においても,元画像のすべてのピクセルを保持)の間の値をとります. StereoRectify を参照してください.
- newCameraMatrix – 出力される新たなカメラ行列.
- newImageSize – 平行化された後の画像サイズ.デフォルトでは imageSize にセットされます.
- validPixROI – オプション出力.歪み補正された画像中のすべての有効なピクセル領域を囲む矩形. StereoRectify の roi1, roi2 の説明を参照してください.
この関数は,フリースケーリングパラメータに基づいて,最適な新しいカメラ行列を求め ます.このパラメータを変化させることで,ユーザは目的に合うピクセルだけを取り出したり alpha=0 ,コーナーを重要視して,すべての元画像ピクセルを保持したり alpha=1 ,あるいはその中間で,何か別のピクセルを得たりします.また, alpha>0 の場合,歪み補正された結果には,補正前の画像の外側にある「仮想」ピクセルに対応した黒いピクセルが含まれる可能性があります.元のカメラ行列,歪み係数,求められた新しいカメラ行列,そして newImageSize は, Remap 用のマップを生成するために InitUndistortRectifyMap に渡されるべきものです.
InitIntrinsicParams2D¶
- void cvInitIntrinsicParams2D(const CvMat* objectPoints, const CvMat* imagePoints, const CvMat* npoints, CvSize imageSize, CvMat* cameraMatrix, double aspectRatio=1.)¶
3次元-2次元の対応点から,カメラの内部パラメータ行列を求めます.
パラメタ: - objectPoints – 物体上の点座評が結合された配列. CalibrateCamera2 を参照してください.
- imagePoints – 物体上の点座標を投影した座標が結合された配列. CalibrateCamera2 を参照してください.
- npoints – 点の個数の配列. CalibrateCamera2 を参照してください.
- imageSize – ピクセル単位で表された画像サイズ.主点を初期化するために利用されます.
- cameraMatrix – 出力されるカメラ行列
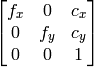
- aspectRatio – これが0以下の場合,
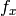 と
と 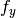 は独立に推定されます.そうでない場合,
は独立に推定されます.そうでない場合, 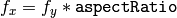 となります.
となります.
この関数は,キャリブレーション処理のためのカメラ行列の初期値を推定します. 現在のところ,平面のキャリブレーション器具,つまり,物体上の点の z-座標=0 となるようなものだけをサポートしています.
InitUndistortMap¶
- void cvInitUndistortMap(const CvMat* cameraMatrix, const CvMat* distCoeffs, CvArr* map1, CvArr* map2)¶
歪み補正マップを求めます.
パラメタ: - cameraMatrix – 入力されるカメラ行列
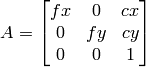
- distCoeffs – 入力される歪み係数ベクトル
![(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6]])](_images/math/7c67b59b59778bc682b2d972bde3d910b2326924.png) .4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます.
.4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます. - map1 – 1番目の出力マップ. 型は CV_32FC1 または CV_16SC2 - 後者の方がより効率的です.
- map2 – 2番目の出力マップ. 型は CV_32FC1 または CV_16UC1 - 後者の方がより効率的です.
- cameraMatrix – 入力されるカメラ行列
この関数は, InitUndistortRectifyMap を単純化した形式です.ここでは,平行化変換 R が単位行列,さらに newCameraMatrix=cameraMatrix となっています.
InitUndistortRectifyMap¶
- void cvInitUndistortRectifyMap(const CvMat* cameraMatrix, const CvMat* distCoeffs, const CvMat* R, const CvMat* newCameraMatrix, CvArr* map1, CvArr* map2)¶
歪み補正および平行化変換のマップを求めます.
パラメタ: - cameraMatrix – 入力されるカメラ行列
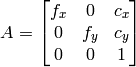
- distCoeffs – 入力される歪み係数ベクトル
![(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6]])](_images/math/7c67b59b59778bc682b2d972bde3d910b2326924.png) .4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます.
.4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます. - R – オプション.物体空間における平行化変換(3x3 の行列).ここでは StereoRectify によって求められた R1 または R2 を渡すことができます.この行列が NULL だった場合,恒等変換が仮定されます.
- newCameraMatrix – 新しいカメラ行列
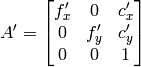
- map1 – 1番目の出力マップ. 型は CV_32FC1 または CV_16SC2 - 後者の方がより効率的です.
- map2 – 2番目の出力マップ. 型は CV_32FC1 または CV_16UC1 - 後者の方がより効率的です.
- cameraMatrix – 入力されるカメラ行列
この関数は,歪み補正変換と平行化変換を結合させた変換を求め,その結果を Remap 用のマップ形式で表現します.歪み補正された画像は,まるで,カメラ行列が =newCameraMatrix である歪みを持たないカメラで撮影したかのような画像に見えます.単眼カメラの場合,通常, newCameraMatrix は cameraMatrix と等しくなるか,あるいはスケーリングを制御する必要があれば GetOptimalNewCameraMatrix によって求められます.ステレオカメラの場合,通常, newCameraMatrix は StereoRectify によって求められた P1 または P2 にセットされます.
また,この新しいカメラは, R に従って,個別に座標空間内での方向が決められます.これにより,例えば,ステレオカメラの両方の画像のエピポーラ線が平行で,同じy-座標を持つように各カメラを揃えることができるようになります (これは,横に並んだステレオカメラの場合です).
この関数は,実際に
Remap
で利用される逆マッピングアルゴリズム用のマップを生成ます.すなわち,この関数は(歪み補正,平行化された)出力画像の各ピクセル
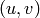 毎に,それに対応する元画像(つまり,カメラからのオリジナル画像)の座標を求めます.その処理は,以下のようになります:
毎に,それに対応する元画像(つまり,カメラからのオリジナル画像)の座標を求めます.その処理は,以下のようになります:
![\begin{array}{l} x \leftarrow (u - {c'}_x)/{f'}_x \\ y \leftarrow (v - {c'}_y)/{f'}_y \\{[X\,Y\,W]} ^T \leftarrow R^{-1}*[x \, y \, 1]^T \\ x' \leftarrow X/W \\ y' \leftarrow Y/W \\ x" \leftarrow x' (1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + 2p_1 x' y' + p_2(r^2 + 2 x'^2) \\ y" \leftarrow y' (1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + p_1 (r^2 + 2 y'^2) + 2 p_2 x' y' \\ map_x(u,v) \leftarrow x" f_x + c_x \\ map_y(u,v) \leftarrow y" f_y + c_y \end{array}](_images/math/b2ef04e09ac8e397d10674839524575bbc2ffb3e.png)
ここで
![(k_1, k_2, p_1, p_2[, k_3])](_images/math/00139c2d6590850e2b07264b39d783c0839b7337.png) は,歪み係数を表します.
は,歪み係数を表します.
ステレオカメラの場合,この関数は,各カメラ毎に1度ずつ,2度呼ばれます. StereoCalibrate の後 StereoRectify が呼ばれ,そしてこの関数が呼び出されます.しかし,ステレオカメラがキャリブレーションされていなかった場合でも, StereoRectifyUncalibrated を用いてF行列から直接,平行化変換を求めることが可能です.この関数は,各カメラに対して,3次元空間における回転行列 R ではなく,ピクセル領域における平行化変換として,ホモグラフィ行列 H を求めます. R は, H から次のようにして求めることができます:
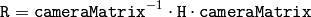
ここで cameraMatrix は,任意に選ぶことができます.
POSIT¶
- void cvPOSIT(CvPOSITObject* posit_object, CvPoint2D32f* imagePoints, double focal_length, CvTermCriteria criteria, CvMatr32f rotationMatrix, CvVect32f translation_vector)¶
POSITアルゴリズムを実行します.
パラメタ: - posit_object – 物体情報構造体へのポインタ.
- imagePoints – 物体点座標の2次元画像平面への投影点,へのポインタ.
- focal_length – 利用されるカメラの焦点距離.
- criteria – POSITアルゴリズムの反復計算に対する停止基準.
- rotationMatrix – 回転行列.
- translation_vector – 並進ベクトル.
この関数は,POSITアルゴリズムの実装です.画像座標は,カメラ座標系で与えられます.また,焦点距離は,カメラキャリブレーション関数を利用して取得できます.このアルゴリズムの各試行において,新たな推定姿勢の透視投影が計算されます.
(前の試行と今の試行の)2つの投影間の差分ノルムは,それぞれに対応する点間の最大距離です.パラメータ criteria.epsilon は,この差が十分小さくなった場合にアルゴリズムを停止するために利用されます.
ProjectPoints2¶
- void cvProjectPoints2(const CvMat* objectPoints, const CvMat* rvec, const CvMat* tvec, const CvMat* cameraMatrix, const CvMat* distCoeffs, CvMat* imagePoints, CvMat* dpdrot=NULL, CvMat* dpdt=NULL, CvMat* dpdf=NULL, CvMat* dpdc=NULL, CvMat* dpddist=NULL)¶
3次元点を画像平面に投影します.
パラメタ: - objectPoints – 3次元物体上の点群座標の入力配列.これは,3xN または Nx3 のシングルチャンネル配列,あるいは 1xN または Nx1 の3チャンネル配列 です.ここで N はビューの点の個数です.
- rvec – 回転ベクトル. Rodrigues2 を参照してください.
- tvec – 並進ベクトル.
- cameraMatrix – カメラ行列
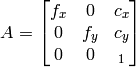
- distCoeffs – 入力される歪み係数ベクトル
![(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6]])](_images/math/7c67b59b59778bc682b2d972bde3d910b2326924.png) .4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます.
.4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます. - imagePoints – 出力される,画像上の点の 2xN または Nx2 の1チャンネル配列,あるいは 1xN または Nx1 の2チャンネル配列.
- dpdrot – オプション.画像点を回転ベクトルの各要素に関して微分した 2Nx3 の行列.
- dpdt – オプション.画像点を並進ベクトルの各要素に関して微分した 2Nx3 の行列.
- dpdf – オプション.画像点を
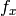 と
と 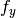 に関して微分した 2Nx2 の行列.
に関して微分した 2Nx2 の行列. - dpdc – オプション.画像点を
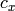 と
と 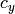 に関して微分した 2Nx2 の行列.
に関して微分した 2Nx2 の行列. - dpddist – オプション.画像点を各歪み係数に関して微分した 2Nx4 の行列.
この関数は,カメラの内部・外部パラメータが与えられると,3次元点を画像平面に投影します. オプションとして,この関数はヤコビ行列,つまり画像点を入力パラメータすべての関数とみなし,特定のカメラパラメータ,内部および/または外部パラメータで偏微分した行列,を求めます. 求められたヤコビ行列は, CalibrateCamera2 , FindExtrinsicCameraParams2 そして StereoCalibrate での大域的最適化において利用されます.この関数自身も,現在の内部・外部パラメータが与えられた場合の再投影誤差を求めるために利用されます.
rvec=tvec=(0,0,0) ,または 3x3 の単位行列にするために distCoeffs=Mat() とセットすることによって,この関数を利用した様々な部分事例を得ることができることに注意してください.つまり,疎な点集合に対する歪んだ座標を求めたり,歪みのない理想的なものとして透視変換を適用したり(そして,その微分を求めたりも)できます.
ReprojectImageTo3D¶
- void cvReprojectImageTo3D(const CvArr* disparity, CvArr* _3dImage, const CvMat* Q, int handleMissingValues=0)¶
視差画像を3次元空間に再投影します.
パラメタ: - disparity – 入力される,シングルチャンネル,16ビット符号付き,または32ビット浮動小数点型の視差画像.
- _3dImage – 出力される,3チャンネルで disparity と同じサイズの浮動小数点型画像. _3dImage(x,y) の各要素には,視差マップから求められた点 (x,y) の3次元座標が格納されます.
- Q – StereoRectify によって得られる
 の透視変換行列.
の透視変換行列. - handleMissingValues – これが真の場合,最小の視差を持つピクセル(これは外れ値に対応します. FindStereoCorrespondenceBM を参照してください)は,非常に大きいZの値(現在は 10000 にセットされています)を持つ3次元点に変換されます.
この関数は,1チャンネルの視差マップを,3次元面を表現する3チャンネルの画像に変換します.つまり,各ピクセル (x,y) と,それに対応する視差 d=disparity(x,y) に対して,次のように計算されます:
![\begin{array}{l} [X \; Y \; Z \; W]^T = \texttt{Q} *[x \; y \; \texttt{disparity} (x,y) \; 1]^T \\ \texttt{\_3dImage} (x,y) = (X/W, \; Y/W, \; Z/W) \end{array}](_images/math/1af29654ff7bcec951f0d0adb80aadf62672fde5.png)
行列
Q
は,例えば,
StereoRectify
によって求められるような任意の
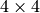 行列です.疎な点集合 {(x,y,d),...} を3次元空間に再投影するためには,
PerspectiveTransform
を利用します.
行列です.疎な点集合 {(x,y,d),...} を3次元空間に再投影するためには,
PerspectiveTransform
を利用します.
RQDecomp3x3¶
- void cvRQDecomp3x3(const CvMat *M, CvMat *R, CvMat *Q, CvMat *Qx=NULL, CvMat *Qy=NULL, CvMat *Qz=NULL, CvPoint3D64f *eulerAngles=NULL)¶
3x3 行列の ‘RQ’ 分解を行います.
パラメタ: - M – 入力される
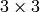 の浮動小数点型行列.
の浮動小数点型行列. - R – 出力される
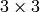 の上三角行列.
の上三角行列. - Q – 出力される
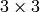 の直行行列.
の直行行列. - Qx – オプション.x-軸周りの 3x3 の回転行列.
- Qy – オプション.y-軸周りの 3x3 の回転行列.
- Qz – オプション.z-軸周りの 3x3 の回転行列.
- eulerAngles – オプション.回転を表す3つのオイラー角.
- M – 入力される
この関数は,ギブンス回転を利用して RQ 分解を行います.これは, DecomposeProjectionMatrix において,射影行列の左 3x3 部分行列を,カメラ行列と回転行列に分解するために利用されます.
またオプションとして,各軸周りの3つの回転行列,そしてOpenGLで利用できる3つのオイラー角を 得ることができます.
ReleasePOSITObject¶
- void cvReleasePOSITObject(CvPOSITObject** posit_object)¶
3次元物体情報構造体を解放します.
パラメタ: - posit_object – 構造体 CvPOSIT へのダブルポインタ.
この関数は,事前に関数 CreatePOSITObject によって確保されたメモリを解放します.
ReleaseStereoBMState¶
- void cvReleaseStereoBMState(CvStereoBMState** state)¶
ブロックマッチングステレオ対応点探索構造体を解放します.
パラメタ: - state – 解放される構造体へのダブルポインタ.
この関数は,ステレオ対応点探索構造体と,関連する内部バッファをすべて解放します.
ReleaseStereoGCState¶
- void cvReleaseStereoGCState(CvStereoGCState** state)¶
グラフカットに基づくステレオ対応点探索アルゴリズムのための状態構造体を解放します.
パラメタ: - state – 解放される構造体へのダブルポインタ.
この関数は,ステレオ対応点探索構造体と,関連する内部バッファをすべて解放します.
Rodrigues2¶
- int cvRodrigues2(const CvMat* src, CvMat* dst, CvMat* jacobian=0)¶
回転行列と回転ベクトルを相互に変換します.
パラメタ: - src – 入力回転ベクトル(3x1 または 1x3),または入力回転行列(3x3).
- dst – 出力回転行列(3x3),または出力回転ベクトル(3x1 または 1x3).
- jacobian – オプションとして出力される, 3x9 または 9x3 のヤコビ行列.出力配列要素を入力配列要素で偏微分したものです.
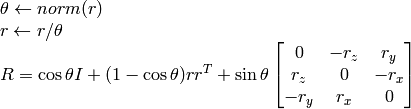
以下の関係から,逆変換も簡単に行うことができます.
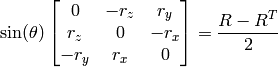
回転ベクトルは,便利で最もコンパクトな回転行列の表現方法です(すべての回転行列は丁度3自由度なので). この表現方法は, CalibrateCamera2 , StereoCalibrate または FindExtrinsicCameraParams2 のような3次元幾何学の大域的最適化処理において利用されます.
StereoCalibrate¶
- double cvStereoCalibrate(const CvMat* objectPoints, const CvMat* imagePoints1, const CvMat* imagePoints2, const CvMat* pointCounts, CvMat* cameraMatrix1, CvMat* distCoeffs1, CvMat* cameraMatrix2, CvMat* distCoeffs2, CvSize imageSize, CvMat* R, CvMat* T, CvMat* E=0, CvMat* F=0, CvTermCriteria term_crit=cvTermCriteria( CV_TERMCRIT_ITER+CV_TERMCRIT_EPS, 30, 1e-6), int flags=CV_CALIB_FIX_INTRINSIC)¶
ステレオカメラのキャリブレーションを行います.
パラメタ: - objectPoints – 物体座標,つまり,モデル座標空間におけるキャリブレーションパターンの特徴点の結合行列.浮動小数点型の 3xN または Nx3 のシングルチャンネル配列,あるいは 1xN または Nx1 の3チャンネル配列です.ここで N は,すべてのビューでの点の総数を表します.
- imagePoints1 – 物体座標の1番目のカメラビューへの投影点の結合行列.浮動小数点型の 2xN または Nx2 のシングルチャンネル配列,あるいは 1xN または Nx1 の2チャンネル配列です.ここで N は,すべてのビューでの点の総数を表します.
- imagePoints2 – 物体座標の2番目のカメラビューへの投影点の結合行列.浮動小数点型の 2xN または Nx2 のシングルチャンネル配列,あるいは 1xN または Nx1 の2チャンネル配列です.ここで N は,すべてのビューでの点の総数を表します.
- pointCounts – 整数型で 1xM または Mx1 のベクトル(ここで Mは,キャリブレーションパターンのビューの個数を表します).この要素は,各ビューに写る座標点の個数です.ベクトル要素の合計値は, objectPoints および imagePoints* のサイズ (=N) と一致しなければいけません.
- cameraMatrix1 – 入出力.1番目のカメラ行列:
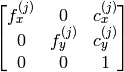 ,
,  もし, CV_CALIB_USE_INTRINSIC_GUESS , CV_CALIB_FIX_ASPECT_RATIO , CV_CALIB_FIX_INTRINSIC あるいは CV_CALIB_FIX_FOCAL_LENGTH のいずれかが指定される場合は,いくつかの,あるいはすべての行列要素が初期化される必要があります.flags の説明を参照してください.
もし, CV_CALIB_USE_INTRINSIC_GUESS , CV_CALIB_FIX_ASPECT_RATIO , CV_CALIB_FIX_INTRINSIC あるいは CV_CALIB_FIX_FOCAL_LENGTH のいずれかが指定される場合は,いくつかの,あるいはすべての行列要素が初期化される必要があります.flags の説明を参照してください. - distCoeffs1 – 入出力.歪み係数ベクトル
![(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6]])](_images/math/7c67b59b59778bc682b2d972bde3d910b2326924.png) .4,5,または8要素となります.
.4,5,または8要素となります. - cameraMatrix2 – 入出力.2番目のカメラ行列.cameraMatrix1 と同様です.
- distCoeffs2 – 入出力.2番目のカメラに対するレンズ歪み係数. distCoeffs1 と同様です.
- imageSize – 画像サイズ.カメラの内部行列を初期化するためだけに利用されます.
- R – 出力される,1番目と2番目のカメラ座標系間の回転行列.
- T – 出力される,それぞれのカメラ座標系間の並進ベクトル.
- E – オプション. 出力されるE行列.
- F – オプション. 出力されるF行列.
- term_crit – 反復最適化アルゴリズムの停止基準.
- flags –
様々なフラグ.0または以下の値の組み合わせです:
- CV_CALIB_FIX_INTRINSIC これが指定された場合, distCoeffs? と同じく cameraMatrix? も固定され, R, T, E と F だけが推定されます
- CV_CALIB_USE_INTRINSIC_GUESS これが指定されると,いくつかの,またはすべての(これは他のフラグに依存します)内部パラメータが最適化されます.しかし,初期値はユーザが与える必要があります
- CV_CALIB_FIX_PRINCIPAL_POINT 最適化の間,主点が固定されます
- CV_CALIB_FIX_FOCAL_LENGTH
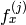 と
と 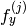 が固定されます
が固定されます - CV_CALIB_FIX_ASPECT_RATIO
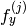 が最適化されますが,比率
が最適化されますが,比率 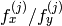 は固定されます
は固定されます - CV_CALIB_SAME_FOCAL_LENGTH 強制的に
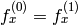 かつ
かつ 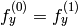 となります
となります - CV_CALIB_FIX_K1,...,CV_CALIB_FIX_K6 最適化中に,指定した半径方向の歪み係数を変更しません. CV_CALIB_USE_INTRINSIC_GUESS が指定されている場合は,与えられた distCoeffs 行列の係数が利用されます.そうでない場合は,0が利用されます.
q * CV_CALIB_RATIONAL_MODEL 係数 k4, k5, k6 を有効にします.後方互換性を保つためには,このフラグを明示的に指定して,キャリブレーション関数が rational モデルを利用して8個の係数を返すようにします.このフラグが指定されない場合,関数は5つの歪み係数のみを計算し ます.
この関数は,ステレオペアを構成する2つのカメラ間の変換を推定します.2つのカメラの相対位置と相対姿勢が固定されたステレオカメラがあり,1番目のカメラと2番目のカメラに対する物体の姿勢 (R1, T1) と (R2, T2) をそれぞれ計算したとすると,これらの姿勢は明らかに互いに関係があります.つまり, (
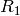 ,
,
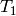 ) が与えられると, (
) が与えられると, (
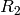 ,
,
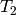 ) を求めることができるので,我々は,2番目のカメラの1番目のカメラに対する位置と姿勢さえ知っていればよいことになります.これが,この関数の働きです.これは (
) を求めることができるので,我々は,2番目のカメラの1番目のカメラに対する位置と姿勢さえ知っていればよいことになります.これが,この関数の働きです.これは (
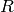 ,
,
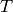 ) を次のように求めます:
) を次のように求めます:
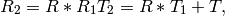
またオプションとして,E 行列を求めます.
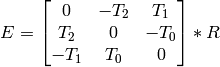
ここで
 は,並進ベクトル
は,並進ベクトル
 :
:
![T=[T_0, T_1, T_2]^T](_images/math/586c8ad76bed1689a0d7d3cf8356439559b1d4de.png) の要素を表します.さらに,この関数は F行列も求めることができます.
の要素を表します.さらに,この関数は F行列も求めることができます.
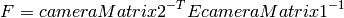
この関数は,ステレオカメラの位置姿勢関係を求めるだけでなく,2つのカメラそれぞれの完全なキャリブレーションも行うことができます.しかし,パラメータ空間の次元が大きすぎる事や,入力データのノイズなどが原因で,最適解を得られない可能性もあります.したがって,各カメラの内部パラメータを(例えば CalibrateCamera2 を用いて)個々に高精度に推定できるならば,そちらの方法が推奨されます.その後に,その計算された内部パラメターと CALIB_FIX_INTRINSIC フラグをこの関数に渡せばよいです.それが無理で,全てのパラメータを一度に計算する場合,いくつかのパラメータに制限を与えると良いでしょう.例えば, CV_CALIB_SAME_FOCAL_LENGTH フラグと CV_CALIB_ZERO_TANGENT_DIST フラグを指定することは,通常は妥当な仮定と言えます.
CalibrateCamera2 と同様に,この関数は,両方のカメラのすべてのビューのすべての点の再投影誤差の和を最小化します. また,この関数は,最終的な再投影誤差を返します.
StereoRectify¶
- void cvStereoRectify(const CvMat* cameraMatrix1, const CvMat* cameraMatrix2, const CvMat* distCoeffs1, const CvMat* distCoeffs2, CvSize imageSize, const CvMat* R, const CvMat* T, CvMat* R1, CvMat* R2, CvMat* P1, CvMat* P2, CvMat* Q=0, int flags=CV_CALIB_ZERO_DISPARITY, double alpha=-1, CvSize newImageSize=cvSize(0, 0), CvRect* roi1=0, CvRect* roi2=0)¶
キャリブレーション済みステレオの,それぞれのカメラの平行化変換を求めます.
パラメタ: - cameraMatrix2 (cameraMatrix1,) – カメラ行列
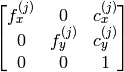 .
. - distCoeffs2 (distCoeffs1,) – 入力される歪み係数ベクトル
![(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6]])](_images/math/7c67b59b59778bc682b2d972bde3d910b2326924.png) .4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます.
.4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます. - imageSize – ステレオキャリブレーションに利用された画像サイズ.
- R – 1番目と2番目のカメラの座標系間の回転行列.
- T – 1番目と2番目のカメラの座標系間の並進ベクトル.
- R2 (R1,) – 出力.それぞれ,1番目と2番目のカメラに対する
 の平行化変換(回転行列).
の平行化変換(回転行列). - P2 (P1,) – 出力.新しい(平行化された)座標系における
 の射影行列.
の射影行列. - Q – 出力.
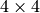 の視差-デプス間のマッピング行列. reprojectImageTo3D() を参照してください.
の視差-デプス間のマッピング行列. reprojectImageTo3D() を参照してください. - flags – 処理フラグ.0または CV_CALIB_ZERO_DISPARITY .このフラグがセットされている場合,関数は各カメラの主点を,平行化されたビューの同じピクセル座標にします.このフラグがセットされていない場合,関数は有効画像領域が最大になるように,画像を水平または垂直方向(これはエピポーラ線の方向に依存します)にずらす場合があります.
- alpha – フリースケーリングパラメータ.これが -1 の場合,関数はデフォルトのスケーリングを行います.そうでない場合,パラメータは0から1の間の値でなくてはいけません. alpha=0 は,有効なピクセルのみが見えるように,平行化された画像を拡大・並進することを意味します(つまり,平行化を行った後には黒い領域が残りません). alpha=1 は,カメラから得られた元画像のすべてのピクセルが平行化後の画像にも残っているように,平行化された画像を縮小・並進することを意味します(つまり,元画像のピクセルがまったく削除されません).もちろん,中間の値は,これらの対極のケースの中間の結果を生成します.
- newImageSize – 平行化後の新しい画像の解像度.これと同じサイズが InitUndistortRectifyMap に渡されるべきです.OpenCV サンプルディレクトリの stereo_calib.cpp を参照してください.デフォルト,つまり (0, 0) が渡された場合は,これは元画像サイズ imageSize にセットされます.より大きな値をセットすると,大きな歪みがある場合は特に,元画像のディテールを保つことができるようになります.
- roi2 (roi1,) – オプション出力.平行化された画像内の,すべてのピクセルが有効である領域を示す矩形. alpha=0 の場合,ROIは画像全体を含みます.そうでない場合,より小さいサイズになるでしょう.以下の図を参照してください.
- cameraMatrix2 (cameraMatrix1,) – カメラ行列
この関数は,各カメラの回転行列を求めます.この回転行列によって,両方のカメラの画像平面が(仮想的に)同一平面に乗るように変換されます.その結果,すべてのエピポーラ線が平行になるので,多数のステレオ対応点探索問題が単純化されます.この関数は, stereoCalibrate() によって求められた行列を入力にとり,2つの回転行列と,新しい座標系における2つの投影行列を出力します.この関数は,次の2つの場合を区別します:
- 水平ステレオ.1番目のカメラと2番目のカメラのビューが互いに,主に x 軸に沿った方向にずれている状態(多少は垂直方向の移動もあるかもしれません).
平行化された画像では,左右のカメラ間のエピポーラ線は,水平,かつ,同じ y-座標(高さ)になる.P1 と P2 は,以下のようになります:
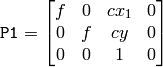
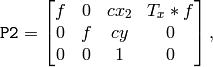
ここで,
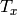 はカメラ間の水平方向のずれであり,
CV_CALIB_ZERO_DISPARITY
がセットされている場合は
はカメラ間の水平方向のずれであり,
CV_CALIB_ZERO_DISPARITY
がセットされている場合は
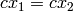 となります.
となります.- 垂直ステレオ.1番目のカメラと2番目のカメラのビューが互いに,主に y 軸に沿った方向にずれている状態(これも,多少は水平方向の移動があるかもしれません).
平行化された画像でのエピポーラ線は,垂直,かつ,同じ x-座標になる.P1 と P2 は,以下のようになります:
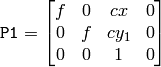
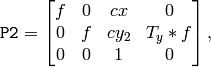
ここで,
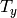 はカメラ間の垂直方向のずれであり,
CALIB_ZERO_DISPARITY
がセットされている場合は
はカメラ間の垂直方向のずれであり,
CALIB_ZERO_DISPARITY
がセットされている場合は
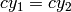 となります.
となります.
見ての通り, P1 と P2 の最初の3列は,「平行化された」新たなカメラ行列そのものです. これらの行列は, R1 および R2 と一緒に InitUndistortRectifyMap に渡して,それぞれのカメラの平行化マップを初期化することができます.
以下は, stereo_calib.cpp サンプルのスクリーンショットです.ここに示される赤い水平線は,対応する画像領域を通過しています.つまり,(多くのステレオ対応点探索アルゴリズムが前提とするように)両方の画像が綺麗に平行化されていることが分かります.また,緑の矩形は, roi1 と roi2 を示し,その中が確かにすべて有効なピクセルであることが分かります.

StereoRectifyUncalibrated¶
- void cvStereoRectifyUncalibrated(const CvMat* points1, const CvMat* points2, const CvMat* F, CvSize imageSize, CvMat* H1, CvMat* H2, double threshold=5)¶
キャリブレーションされていないステレオカメラの,それぞれのカメラの平行化変換を求めます.
パラメタ: - points2 (points1,) – 対応する2次元点を表すの2つの配列. FindFundamentalMat でサポートされるものと同じフォーマットです.
- F – 入力されるF行列. FindFundamentalMat を利用して,これと同じ点ペアの集合から計算することができます.
- imageSize – 画像サイズ.
- H2 (H1,) – 出力される,1番目と2番目の画像に対する平行化ホモグラフィ行列.
- threshold – 外れ値を除外するために用いられるオプションの閾値.このパラメータが0より大きい場合,ホモグラフィ行列を計算する前に,エピポーラ幾何に十分に従わない(つまり,
![|\texttt{points2[i]}^T*\texttt{F}*\texttt{points1[i]}|>\texttt{threshold}](_images/math/e77a03eb53f034dff5b0581485e41f7339b205bf.png) となる)すべての点ペアが棄却されます.そうでない場合,つまりパラメータが0以下の場合は,すべての点がインライアであると見なされます.
となる)すべての点ペアが棄却されます.そうでない場合,つまりパラメータが0以下の場合は,すべての点がインライアであると見なされます.
この関数は,カメラの内部パラメータや空間の相対的位置を必要とすることなく,平行化変換を求めます.なので,「Uncalibrated」という接尾辞がついています. StereoRectify とのもう1つの違いとして,関数の出力が,物体(3次元)空間における平行化変換ではなく,ホモグラフィ行列 H1 と H2 によってエンコードされた平面透視変換となることが挙げられます.この関数は,アルゴリズム Hartley99 の実装です.
このアルゴリズムは,カメラの内部パラメータを知る必要はありませんが,エピポーラ幾何に大きく依存していることに注意してください.したがって,カメラレンズが大きく歪んでいる場合は,F行列を計算してこの関数を呼び出すよりも前に,歪みを補正しておくのが賢明です.例えば,ステレオの各カメラの歪み係数は, CalibrateCamera2 を用いて個別に推定できます.画像ならば Undistort2 によって,点座標だけならば UndistortPoints によって補正することが可能です.
Undistort2¶
- void cvUndistort2(const CvArr* src, CvArr* dst, const CvMat* cameraMatrix, const CvMat* distCoeffs, const CvMat* newCameraMatrix=0)¶
レンズ歪みを補正するように画像を変形させます.
パラメタ: - src – (歪んだ)入力画像.
- dst – (補正された)出力画像. src と同じサイズ,同じ型.
- cameraMatrix – 入力されるカメラ行列
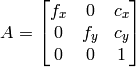
- distCoeffs – 入力される歪み係数ベクトル
![(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6]])](_images/math/7c67b59b59778bc682b2d972bde3d910b2326924.png) .4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます.
.4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます.
この関数は,半径方向および円周方向のレンズ歪みを補正するように画像を変換します.
この関数は,単に InitUndistortRectifyMap ( R は単位行列)と Remap (バイリニア補間)を組み合わせたものです.変換の詳細については,前述の関数を参照してください.
元画像に対応するピクセルが存在しないような出力画像のピクセルは,0(黒色)で埋められます.
補正された画像内に残っている元画像の部分画像は newCameraMatrix で制御できます.ユーザは,必要に応じた適切な newCameraMatrix を求めるために GetOptimalNewCameraMatrix を利用することができます.
これらのカメラ行列と歪みパラメータは
CalibrateCamera2
を用いて決定できます.
画像の解像度がキャリブレーション時と異なる場合,歪み係数はそのままで構いませんが,
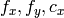 および
および
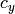 を適宜スケーリングする必要があります
を適宜スケーリングする必要があります
UndistortPoints¶
- void cvUndistortPoints(const CvMat* src, CvMat* dst, const CvMat* cameraMatrix, const CvMat* distCoeffs, const CvMat* R=NULL, const CvMat* P=NULL)¶
観測された点座標から,理想的な点座標を求めます.
パラメタ: - src – 観測された点座標. 1xN または Nx1 で 2チャンネル(CV _ 32FC2 or CV _ 64FC2).
- dst – 歪み補正および逆透視変換された後に出力される,理想的な点座標. src と同じフォーマット.
- cameraMatrix – カメラ行列
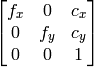
- distCoeffs – 入力される歪み係数ベクトル
![(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6]])](_images/math/7c67b59b59778bc682b2d972bde3d910b2326924.png) .4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます.
.4,5,または8要素となります.このベクトルが NULL または空である場合,歪み係数は0であると見なされます. - R – 物体空間における平行化変換(3x3 の行列). StereoRectify() によって求められる R1 または R2 のどちらかが,ここに渡されます.この行列が空の場合,単位行列が変換行列として利用されます.
- P – 新たなカメラ行列(3x3)または,新たな射影行列(3x4). StereoRectify() によって求められる P1 or P2 のどちらかが,ここに渡されます.この行列がemptyの場合,単位行列が新たなカメラ行列として利用されます.
この関数は, Undistort2 や InitUndistortRectifyMap と似ていますが,ラスタ画像の代わりに,疎な点集合を扱います.また, ProjectPoints2 に対する逆変換のような処理も行います(3次元物体の場合は,当然その3次元座標を再構成するわけではありません.しかし,平面物体の場合は,適切な R が指定されれば,並進ベクトル次第で,そのようなことも起こります).
// (u,v) は入力点座標, (u', v') は出力点座標
// camera_matrix=[fx 0 cx; 0 fy cy; 0 0 1]
// P=[fx' 0 cx' tx; 0 fy' cy' ty; 0 0 1 tz]
x" = (u - cx)/fx
y" = (v - cy)/fy
(x',y') = undistort(x",y",dist_coeffs)
[X,Y,W]T = R*[x' y' 1]T
x = X/W, y = Y/W
u' = x*fx' + cx'
v' = y*fy' + cy',
ここで undistort() は,正規化された歪んだ点座標から,正規化されたオリジナルの点座標を推定する,反復近似アルゴリズムです(「正規化された」というのは,座標がカメラ行列に依存しないという意味です).
この関数は,ステレオの各カメラや単眼カメラに対して用いることができます(Rは NULL ).
ヘルプとフィードバック
お探しの情報が見つかりませんか?- ユーザグループ/メーリングリスト (英語)で質問してみてください.
- このドキュメントに誤りなどを見つけたらbug report まで報告してください.また,日本語訳に関する誤りや指摘はOpenCV.jpまでお願いします.
