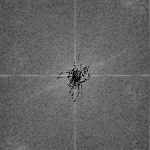
2次元フーリエ変換，フーリエ逆変換

Posted by idojun 17 6月 2010 Under: opencv2.x-samples

YouTube で見た以下のビデオが面白かったので，似たようなものを OpenCV のサンプルとして作ってみました．cv::dft，cv::idft を利用しています．処理の詳細は，ビデオをご覧ください．

C++

001

002

003

004

005

006

007

008

009

010

011

012

013

014

015

016

017

018

019

020

021

022

023

024

025

026

027

028

029

030

031

032

033

034

035

036

037

038

039

040

041

042

043

044

045

046

047

048

049

050

051

052

053

054

055

056

057

058

059

060

061

062

063

064

065

066

067

068

069

070

071

072

073

074

075

076

077

078

079

080

081

082

083

084

085

086

087

088

089

090

091

092

093

094

095

096

097

098

099

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

200

201

202

203

#include <iostream>
#include <cv.h>
#include <highgui.h>
 
using namespace cv;
using namespace std;
 
// class declaration
class DftIdftApp {
public:
  DftIdftApp(const string filename);
  ~DftIdftApp(){};
  void calcMagImage();
  void showOrgImage(){imshow(org_win, src_img);}
  void showMagImage(){imshow(mag_win, mag_img);}
  void showIDFTImage(){imshow(idft_win, idft_img);}
  void shiftDFT(Mat &src, Mat &dst);
  void calcIDFT(bool all=false);
  void clear(){idft_img.setTo(0);}
  static void onMouse(int event, int x, int y, int flags, void* param);
private:
  Mat src_img, mag_img;
  Mat Re_img, Im_img, Complex_img;
  Mat zero, dft_src, dft_dst, dft_dst_p;
  Mat idft_img;
  vector<Mat> mv;
  string org_win, mag_win, idft_win;
  int src_cols, src_rows, dft_cols, dft_rows;
};
 
// constructor
DftIdftApp::DftIdftApp(const string filename)
  :org_win("Original"), mag_win("Magnitude"), idft_win("IDTF")
{
  src_img = imread(filename, 0);
  if(!src_img.data) return;
 
  Size s_size = src_img.size();
  src_cols = s_size.width;
  src_rows = s_size.height;
  Re_img = Mat(s_size, CV_64F);
  Im_img = Mat::zeros(s_size, CV_64F);
  Complex_img = Mat(s_size, CV_64FC2);
   
  src_img.convertTo(Re_img, CV_64F);
  mv.push_back(Re_img);
  mv.push_back(Im_img);
  merge(mv, Complex_img);
  idft_img = zero = Mat::zeros(s_size, CV_64F);
 
  namedWindow(org_win, CV_WINDOW_AUTOSIZE);
  namedWindow(mag_win, CV_WINDOW_AUTOSIZE);
  namedWindow(idft_win, CV_WINDOW_AUTOSIZE);
  cvSetMouseCallback(mag_win.c_str(), DftIdftApp::onMouse, this);
}
 
// calc magnitude image
void
DftIdftApp::calcMagImage()
{
  dft_rows = getOptimalDFTSize(src_rows);
  dft_cols = getOptimalDFTSize(src_cols);
  dft_src = Mat::zeros(dft_rows, dft_cols, CV_64FC2);
   
  Mat roi(dft_src, Rect(0, 0, src_cols, src_rows));
  Complex_img.copyTo(roi);
 
  dft(dft_src, dft_dst);
  dft_dst_p = Mat::zeros(dft_dst.size(), dft_dst.type());
 
  //split(dft_dst.mul(dft_dst), mv);
  //sqrt(mv[0]+mv[1], mv[0]);
  split(dft_dst, mv);
  magnitude(mv[0], mv[1], mv[0]);
  log(mv[0]+1, mv[0]); // for ver. 2.1 or later
    
  shiftDFT(mv[0], mv[0]);
 
  //double min, max;
  //minMaxLoc(mv[0], &min, &max);
  //mag_img = mv[0]*1.0/(max-min) - 1.0*min/(max-min);
  normalize(mv[0], mag_img, 0, 1, CV_MINMAX);
}
 
// swap 1,3 and 2,4 quadrants respectively
void
DftIdftApp::shiftDFT(Mat &src, Mat& dst)
{
  Mat tmp;
  int cx = src.cols/2;
  int cy = src.rows/2;
 
  for(int i=0; i<=cx; i+=cx) {
    Mat qs(src, Rect(i^cx,0,cx,cy));
    Mat qd(dst, Rect(i,cy,cx,cy));
    qs.copyTo(tmp);
    qd.copyTo(qs);
    tmp.copyTo(qd);
  }
}
 
// mouse event callback
void
DftIdftApp::onMouse(int event, int x, int y, int flags, void* param)
{
  DftIdftApp *app = static_cast<DftIdftApp*>(param);
  Mat &dft_dst = app->dft_dst;
  Mat &dft_dst_p = app->dft_dst_p;
  Mat &mag_img = app->mag_img;
  int cx = app->src_cols/2;
  int cy = app->src_rows/2;
  int mx=x, my=y;
  int w = app->dft_cols;
  int h = app->dft_rows;
 
  switch(event) {
  case CV_EVENT_MOUSEMOVE:
    if((flags&CV_EVENT_FLAG_LBUTTON)==0) return;
  case CV_EVENT_LBUTTONUP:
    if(flags&CV_EVENT_FLAG_CTRLKEY) { // LeftButton+CTRL
      int step = 5;
      for(int j=-step; j<=step; j++) {
        my = y+j + ((y+j)<cy ? cy:-cy);
        if(y+j<0 || y+j>=h) continue;
        double *from = dft_dst.ptr<double>(my);
        double *to = dft_dst_p.ptr<double>(my);
        double *mag = mag_img.ptr<double>(y+j);
        for(int i=-step; i<=step; i++) {
          mx = x+i + ((x+i)<cx ? cx:-cx);
          if(x+i<0 || x+i>=w) break;
          to[(mx)*2+0] = from[(mx)*2+0];
          to[(mx)*2+1] = from[(mx)*2+1];
          mag[x+i] = 0;
        }
      }
    } else {  // LeftButton
      mx += x<cx ? cx:-cx;
      my += y<cy ? cy:-cy;
      double *from = dft_dst.ptr<double>(my);
      double *to = dft_dst_p.ptr<double>(my);
      double *mag = mag_img.ptr<double>(y);
      to[(mx)*2+0] = from[(mx)*2+0];
      to[(mx)*2+1] = from[(mx)*2+1];
      mag[x] = 0;
    }
    break;
  default:
    return;
  }
  app->calcIDFT();  
}
 
// Inverse Discrete Fourier Transforma
void
DftIdftApp::calcIDFT(bool all)
{
  if(all) {
    dft_dst.copyTo(dft_dst_p);
    mag_img.setTo(0);
  }
 
  double min, max;
  idft(dft_dst_p, dft_src);
  split(dft_src, mv);
  minMaxLoc(mv[0], &min, &max);
  idft_img = Mat(mv[0]*1.0/max, Rect(0, 0, src_cols, src_rows));
}
 
int
main(int argc, char *argv[])
{
  const string filename = argc > 1 ? argv[1] : "../image/Fourier.png";
  DftIdftApp app(filename);
 
  cout << "Usage: click or drag on Magnitude Image.\n" <<
    "Hot keys: \n"
    "\tESC - quit the program\n"
    "\ta - select all pixels\n"
    "\tr - restore original images\n"
    "\tleft mouse button - select one pixel\n"
    "\tCTRL+left mouse button - select a pixel and neighbors\n";
 
  app.showOrgImage();
  app.calcMagImage();
  while(1) {
    int c = waitKey(10);
    switch((char)c) {
    case '\x1b': // exit
      return 0;
    case 'a': // IDFT all
      app.calcIDFT(true);
      break;
    case 'r': // reset
      app.clear();
      app.calcMagImage();
      break;
    }
    app.showIDFTImage();
    app.showMagImage();
  }
 
  return 0;
}