カメラキャリブレーションと3次元再構成¶
このセクションで述べる関数は,いわゆるピンホールカメラモデルを取り扱います.つまりこのモデルでは,3次元座点を透視投影変換を用いて画像平面に射影することで,シーンのビューが構成されています.
![s \; m' = A [R|t] M'](_images/math/765aba62c7cb09fd36c1b44f3a2e422a28c4ec70.png)
または
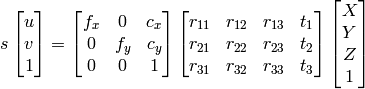
ここで
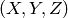 はワールド座標系の3次元座標を表し
はワールド座標系の3次元座標を表し
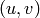 は画像平面に投影された点の座標を表します.
は画像平面に投影された点の座標を表します.
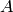 は,カメラ行列,またはカメラの内部パラメータ行列と呼ばれます.
は,カメラ行列,またはカメラの内部パラメータ行列と呼ばれます.
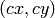 は主点(通常は画像中心),
は主点(通常は画像中心),
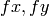 はピクセル単位で表される焦点距離です.
したがって,
あるファクタによってカメラ画像がスケーリングされている場合,
このすべてのパラメータを同じファクタでスケーリング(それぞれが,拡大または縮小)する必要があります.
内部パラメータ行列はビューに依存しないので,一度推定すれば(ズームレンズの場合)焦点距離を固定している限りは繰返し使用することができます.
並進-回転の同次変換行列である
はピクセル単位で表される焦点距離です.
したがって,
あるファクタによってカメラ画像がスケーリングされている場合,
このすべてのパラメータを同じファクタでスケーリング(それぞれが,拡大または縮小)する必要があります.
内部パラメータ行列はビューに依存しないので,一度推定すれば(ズームレンズの場合)焦点距離を固定している限りは繰返し使用することができます.
並進-回転の同次変換行列である
![[R|t]](_images/math/2ec354f9c8316cb3d69be8ceb97c53180a29640e.png) は,外部パラメータ行列と呼ばれます.
これは,静的環境に対するカメラの動き,または逆に,固定カメラの前の物体の剛体運動を表します.
つまり
は,外部パラメータ行列と呼ばれます.
これは,静的環境に対するカメラの動き,または逆に,固定カメラの前の物体の剛体運動を表します.
つまり
![[R|t]](_images/math/2ec354f9c8316cb3d69be8ceb97c53180a29640e.png) は,点座標
は,点座標
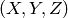 をそれぞれのカメラの座標系に変換します.
上述の変換は,以下の式(で
をそれぞれのカメラの座標系に変換します.
上述の変換は,以下の式(で
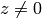 の場合)と等価です.
の場合)と等価です.
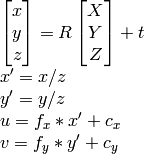
実際のカメラレンズは,主に半径方向の歪みや,わずかに円周方向の歪みを持っているので,上のモデルは以下のように拡張されます.
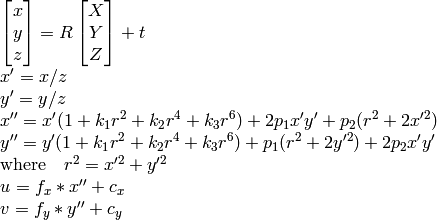
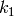 ,
,
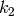 ,
,
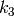 は半径方向の歪み係数,
は半径方向の歪み係数,
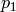 ,
,
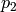 は円周方向の歪み係数です.
は円周方向の歪み係数です.
OpenCV では高次の係数は考慮されません.以降の関数では,歪み係数は
![(k_1, k_2, p_1, p_2[, k_3])](_images/math/4972eec50bbe577c72b5d258e682495024072d5f.png)
というベクトルとして,渡されたり返されたりします.つまり,ベクトルが4つの要素をもつならば,
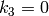 であることを意味します.
であることを意味します.
歪み係数はシーンのビューに依存しないので,カメラの内部パラメータに属します.
また,キャプチャされた画像の解像度に関わらず同じ値のままになります.
つまり,例えば,あるカメラが
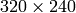 の画像でキャリブレーションされた場合,同じカメラの
の画像でキャリブレーションされた場合,同じカメラの
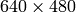 の画像に対してもまったく同じ歪み係数を用いることができます
(
の画像に対してもまったく同じ歪み係数を用いることができます
(
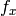 ,
,
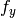 ,
,
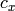 ,
,
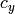 は適切にスケーリングされなければいけませんが).
は適切にスケーリングされなければいけませんが).
以降の関数は,このようなモデルを用いて,次のようなことを行います:
- 内部パラメータ,外部パラメータが与えられた場合に,3次元座標を画像平面上に投影します.
- 内部パラメータ,少数の3次元点,その投影点が与えられた場合に,外部パラメータを求めます.
- 既知のキャリブレーションパターンを写した複数のビュー(つまり,各ビューが,複数の3次元点と2次元点の対応として記述できます)から,カメラの内部パラメータ,外部パラメータを推定します.
- ステレオカメラ「ヘッド」の相対位置と相対姿勢を推定し,カメラの光軸を平行にする 平行化 変換を求めます.
cv::calibrateCamera¶
- double calibrateCamera(const vector<vector<Point3f> >& objectPoints, const vector<vector<Point2f> >& imagePoints, Size imageSize, Mat& cameraMatrix, Mat& distCoeffs, vector<Mat>& rvecs, vector<Mat>& tvecs, int flags=0)¶
キャリブレーションパターンを写した複数のビューから,カメラの内部・外部パラメータを求めます.
パラメタ: - objectPoints – キャリブレーション器具上の点群座標(座標系は器具固定)を表すベクトル,のベクトル.1つのベクトルが,器具の1つのビューを表します.同じキャリブレーション器具がそれぞれのビューに完全に写っている場合,(それぞれのビューの順序を入れ替えたとしても)その座標ベクトルはすべて同じにできます.点群は3次元ですが,器具に固定された座標系上にあるので,もしその器具が平面ならば,器具平面とXY 座標平面とを一致させて点群の Z-座標が0になるようにするのは適切なやり方と言えます
- imagePoints – キャリブレーション器具上の点を,そのビューへ投影した点のベクトル,のベクトル.1つのビューに対して1つのベクトルになります.この投影点は,対応する器具上の点と同じ順序でなければいけません
- imageSize – 画像サイズ.カメラの内部行列を初期化するためだけに利用されます
- cameraMatrix – 入出力用の,カメラの内部パラメータ行列
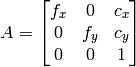 . CV_CALIB_USE_INTRINSIC_GUESS および/または CV_CALIB_FIX_ASPECT_RATIO が指定される場合, fx, fy, cx, cy のいくつか,あるいはすべてが初期化されていなければなりません
. CV_CALIB_USE_INTRINSIC_GUESS および/または CV_CALIB_FIX_ASPECT_RATIO が指定される場合, fx, fy, cx, cy のいくつか,あるいはすべてが初期化されていなければなりません - distCoeffs – 5x1 または 1x5 の歪み係数
![(k_1, k_2, p_1, p_2[, k_3])](_images/math/00139c2d6590850e2b07264b39d783c0839b7337.png) の出力ベクトル
の出力ベクトル - rvecs – 出力される ベクトル .各ビューにおいて推定された回転ベクトルを表します( Rodrigues2 を参照してください).つまり,k番目の回転ベクトルとk番目の並進ベクトル(下の出力パラメータの説明を参照してください)によって,キャリブレーションパターンが,モデル座標空間(物体上の点が指定される空間)からワールド座標空間,つまり,k番目のビューにおけるキャリブレーションパターンの実際の位置に移動することになります(k=0.. M -1)
- tvecs – 出力される ベクトル .各ビューにおいて推定された並進ベクトルを表します
- flags –
様々なフラグ.0,あるいは以下の値の組み合わせ:
- CV_CALIB_USE_INTRINSIC_GUESS cameraMatrix が fx, fy, cx, cy の有効な初期値を含み,これらが最適化されます.そうでない場合は, (cx, cy) には初期値として画像中心(これは入力の imageSize から求められます)がセットされ,焦点距離は最小二乗法で計算されます.もし内部パラメータが既知ならば,外部パラメータを推定するためだけにこの関数を使う必要はないことに注意してください.代わりに FindExtrinsicCameraParams2 を利用しましょう
- CV_CALIB_FIX_PRINCIPAL_POINT 大域的最適化中に,主点が変更されません.主点は画像中心か,あるいは CV_CALIB_USE_INTRINSIC_GUESS が同時にセットされている場合は,別のの指定位置にとどまります
- CV_CALIB_FIX_ASPECT_RATIO この関数は fy だけを自由パラメータとみなして,入力の cameraMatrix で指定された比率 fx/fy を保ちます. CV_CALIB_USE_INTRINSIC_GUESS がセットされていない場合, fx と fy の実際の入力値は無視され,その比率だけが計算されて利用されます
- CV_CALIB_ZERO_TANGENT_DIST 円周方向の歪み係数
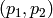 が0にセットされ,そのまま変更されません
が0にセットされ,そのまま変更されません
この関数は,カメラの内部パラメータ,および各ビューにおける外部パラメー タを推定します.各画像における,3次元点の座標と,それに対応する2次元の 投影点の座標を指定する必要があります.これは,幾何的な特徴が既知で,容 易に特徴点を検出できるような物体を用いて行われます.
そのような物体は,キャリブレーション器具またはキャリブレーションパターンと呼ばれます.OpenCVは元々,キャリブレーション器具としてチェスボードをサポートしています( FindChessboardCorners を参照してください).現在のところ,内部パラメータの初期化は,(物体上の点群のz-座標がすべて0になる)平面キャリブレーションパターンに対してのみ実装されています( CV_CALIB_USE_INTRINSIC_GUESS がセットされない場合).初期 cameraMatrix が与えられれば,3次元のキャリブレーション器具も利用することができます.
このアルゴリズムは,次のようになります:
- まず,内部パラメータの初期値を,計算する(これは,平面キャリブレーションパターンを利用した場合のみ可能)か,あるいは入力パラメータから読み込みます.歪み係数は,( CV_CALIB_FIX_K? で指定されているものを除いて)すべて0にセットされます.
- 内部パラメータが既知であるかのように,カメラの初期姿勢を推定します.この推定には, FindExtrinsicCameraParams2 を利用します.
- 再投影誤差を最小にするように,大域的な Levenberg-Marquardt 最適化アルゴリズムが実行されます.つまり,観測された特徴点 imagePoints と,(内部パラメータとカメラ姿勢の現在の推定値を利用した)投影点 objectPoints との距離の2乗和を最小にします. ProjectPoints2 を参照してください.
この関数は,最終的な再投影誤差を返します.
注意:正方ではない(NxN ではない)グリッドを使用して,
findChessboardCorners()
でキャリブレーションを行う場合に,
calibrateCamera
が不正な値(つまり,歪み係数が0,画像中心が
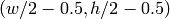 から遠く離れている,さらに/または,
から遠く離れている,さらに/または,
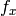 と
と
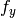 が大きく異なる(比率が 10:1 以上))を返すとすると,
FindChessboardCorners
で
patternSize=cvSize(rows,cols)
としている可能性があります.正しくは,
patternSize=cvSize(cols,rows)
となります.
が大きく異なる(比率が 10:1 以上))を返すとすると,
FindChessboardCorners
で
patternSize=cvSize(rows,cols)
としている可能性があります.正しくは,
patternSize=cvSize(cols,rows)
となります.
参考: FindChessboardCorners , FindExtrinsicCameraParams2 , initCameraMatrix2D() , StereoCalibrate , Undistort2
cv::calibrationMatrixValues¶
- void calibrationMatrixValues(const Mat& cameraMatrix, Size imageSize, double apertureWidth, double apertureHeight, double& fovx, double& fovy, double& focalLength, Point2d& principalPoint, double& aspectRatio)¶
カメラ行列から,有用なカメラ特性を求めます.
パラメタ: - cameraMatrix – カメラの内部パラメータ行列. calibrateCamera() あるいは stereoCalibrate() によって推定できます
- imageSize – ピクセル単位で表された入力画像サイズ
- apertureWidth – センサの物理的な幅
- apertureHeight – センサの物理的な高さ
- fovx – 出力される,水平軸に沿った画角(度単位)
- fovx – 出力される,垂直軸に沿った画角(度単位)
- focalLength – mm単位で表されたレンズの焦点距離
- prinicialPoint – ピクセル単位で表された主点
- aspectRatio –
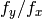
この関数は,あらかじめ推定されたカメラ行列から,様々な役立つカメラ特性を計算します.
cv::composeRT¶
- void composeRT(const Mat& rvec1, const Mat& tvec1, const Mat& rvec2, const Mat& tvec2, Mat& rvec3, Mat& tvec3)¶
- void composeRT(const Mat& rvec1, const Mat& tvec1, const Mat& rvec2, const Mat& tvec2, Mat& rvec3, Mat& tvec3, Mat& dr3dr1, Mat& dr3dt1, Mat& dr3dr2, Mat& dr3dt2, Mat& dt3dr1, Mat& dt3dt1, Mat& dt3dr2, Mat& dt3dt2)
2つの 回転-並進変換を結合します.
パラメタ: - rvec1 – 1番目の回転ベクトル
- rvec1 – 1番目の回転ベクトル
- rvec2 – 2番目の回転ベクトル
- tvec2 – 2番目の並進ベクトル
- rvec3 – 出力.重ね合わされた変換の回転ベクトル
- tvec3 – 出力.重ね合わされた変換の並進ベクトル
- d??d?? – オプション出力. rvec? または tvec? に関する rvec3 または tvec3 の微分
この関数は,以下を求めます.
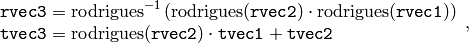
ここで
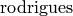 は,回転ベクトルを回転行列に変換する記法であり,
は,回転ベクトルを回転行列に変換する記法であり,
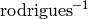 はその逆変換を表しています.
Rodrigues()
を参照してください.
はその逆変換を表しています.
Rodrigues()
を参照してください.
また,この関数はオプションとして,出力ベクトルの入力ベクトルに関する微分を計算することもできます( matMulDeriv() を参照してください). stereoCalibrate() は内部でこの関数を利用していますが,Levenberg-Marquardt 法や他の勾配ベースのソルバを扱うユーザ自身のコードでも,行列の積を含む関数を最適化するためにこの関数を利用することができます.
cv::computeCorrespondEpilines¶
- void computeCorrespondEpilines(const Mat& points, int whichImage, const Mat& F, vector<Vec3f>& lines)¶
ステレオペアの片方の画像上の点に対して,それに対応する別の画像上のエピポーラ線を求めます.
パラメタ: - points – 入力点. CV_32FC2 型で
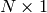 または
または 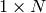 の行列.あるいは vector<Point2f>
の行列.あるいは vector<Point2f> - whichImage – points を含む画像のインデックス(1または2)
- F – FindFundamentalMat または StereoRectify によって指定されるF行列
- lines – 各点に対応した,もう片方の画像上のエピポーラ線が出力されるベクトル. 各エピポーラ線
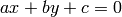 は,3つの数値
は,3つの数値 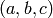 で符号化されます
で符号化されます
- points – 入力点. CV_32FC2 型で
この関数は,ステレオペアの2つの画像の片方に存在する点それぞれに対して,対応する別の画像上のエピポーラ線を求めます.
F行列の定義から(
FindFundamentalMat
を参照してください),1番目の画像(つまり,
whichImage=1
)上の点
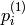 に対する,2番目の画像上の線
に対する,2番目の画像上の線
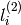 は次のように求められます:
は次のように求められます:
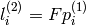
そして,逆に
whichImage=2
の場合,
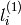 は,
は,
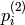 から,次のように求められます:
から,次のように求められます:
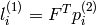
エピポーラ線の係数には,スケールが定義されています.これらは
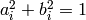 というように正規化されます.
というように正規化されます.
cv::convertPointsHomogeneous¶
- void convertPointsHomogeneous(const Mat& src, vector<Point3f>& dst ) void convertPointsHomogeneous( const Mat& src, vector<Point2f>& dst)¶
点座標と同次座標を,互いに変換します.
パラメタ: - src – 2次元または3次元点の,入力配列または入力ベクトル
- dst – 3次元または2次元点の出力配列
これらの関数は, 2次元または3次元の点と,同次座標を相互に変換,あるいは単に コピーや転置 を行います.入力配列の次元数が出力よりも大きい場合は,各座標値が最後の座標値で割られます:
![\begin{array}{l} (x,y[,z],w) -> (x',y'[,z']) \\ \text{where} \\ x' = x/w \\ y' = y/w \\ z' = z/w \quad \text{(if output is 3D)} \end{array}](_images/math/8da5c69bcb6b6386781ae5cdcd555ed70460e785.png)
出力配列の次元数の方が大きい場合は,各入力点に値1が付け加えられます.それ以外の場合は単に,入力配列が出力配列にコピーされます(転置することもできます).
cv::decomposeProjectionMatrix¶
- void decomposeProjectionMatrix(const Mat& projMatrix, Mat& cameraMatrix, Mat& rotMatrix, Mat& transVect)¶
- void decomposeProjectionMatrix(const Mat& projMatrix, Mat& cameraMatrix, Mat& rotMatrix, Mat& transVect, Mat& rotMatrixX, Mat& rotMatrixY, Mat& rotMatrixZ, Vec3d& eulerAngles)
射影行列を,回転行列とカメラ行列に分解します.
パラメタ: - ProjMatrix – 3x4 の入力射影行列 P
- cameraMatrix – 3x3 の出力カメラ行列 K
- rotMatrix – 3x3 の出力回転行列 R
- transVect – 4x1 の出力並進ベクトル T
- rotMatrX – オプション.3x3 の x-軸周りの回転行列
- rotMatrY – オプション.3x3 の y-軸周りの回転行列
- rotMatrZ – オプション.3x3 の z-軸周りの回転行列
- eulerAngles – オプション.回転を表す3つのオイラー角
この関数は,射影行列をカメラ行列と回転行列,カメラの位置に分解します.
またオプションとして,各軸周りの3つの回転行列,そしてOpenGLで利用できる3つのオイラー角を得ることができます.
この関数は, RQDecomp3x3 に基づいています.
cv::drawChessboardCorners¶
- void drawChessboardCorners(Mat& image, Size patternSize, const Mat& corners, bool patternWasFound)¶
検出されたチェスボードのコーナーを描画します.
パラメタ: - image – 出力画像.8ビットのカラー画像
- patternSize – チェスボード内の,行と列毎の内側コーナー数.(patternSize = cvSize(points _ per _ row,points _ per _ colum) = cvSize(columns,rows) )
- corners – 検出されたコーナーの配列
- patternWasFound – チェスボードが完全に検出された か否 かを示します.ここでは単に FindChessboardCorners の戻り値を渡すことができます
この関数は,検出された個々のチェスボードを描画します.チェスボードが不完全に検出された場合は,コーナーが赤い丸で描画され,完全に検出された場合は,色付きのコーナーが線で結ばれます.
cv::findChessboardCorners¶
- bool findChessboardCorners(const Mat& image, Size patternSize, vector<Point2f>& corners, int flags=CV_CALIB_CB_ADAPTIVE_THRESH+ CV_CALIB_CB_NORMALIZE_IMAGE)¶
チェスボードの内側コーナー位置を求めます.
パラメタ: - image – チェスボードのビュー.8ビットグレースケール画像,またはカラー画像でなければいけません
- patternSize – チェスボードの行と列毎の,内側コーナーの個数( patternSize = cvSize(points _ per _ row,points _ per _ colum) = cvSize(columns,rows) )
- corners – 検出されたコーナーの出力配列
- flags –
様々な処理フラグ.0または以下の値の組み合わせ:
- CV_CALIB_CB_ADAPTIVE_THRESH 入力画像を白黒画像に変換する際に,(画像の明るさの平均値から計算された)固定閾値の代わりに適応的閾値を利用します.
- CV_CALIB_CB_NORMALIZE_IMAGE 固定あるいは適応的閾値を適用する前に, EqualizeHist を用いて画像のガンマ値を正規化します
- CV_CALIB_CB_FILTER_QUADS 輪郭抽出の際に検出された誤った四角を除外するために,(輪郭領域面積,周囲長,正方形度合い,のような)追加の基準を利用します
この関数は,入力画像がチェスボードパターンを写すビューであるかどうかを判断し,もしそうならば,チェスボードの内側コーナーの位置を検出しようとします.これは,すべてのチェスボードコーナーが検出された場合は真値を返し,そのコーナーは特定の順序(1行ごとに,各行は左から右に)で格納されます.そうでない場合,つまり,コーナーの完全な検出や順序づけに失敗した場合は,0を返します.例えば,標準的なチェスボードは, 8 x 8 マスで 7 x 7 個の内側コーナー,つまり黒い正方形が別の黒い正方形と接触する点,をもちます.検出される座標は近似されたもので,より正確な位置を決定するために,関数 FindCornerSubPix を利用する場合があります.
注意: この関数では,様々な環境下でロバストな検出を行うために,チェスボードの周囲に(太い枠淵のような,広ければ広いほど良い)空白が必要です(もし,この空白がなく背景が暗ければ,外側の黒い正方形が適切に分離されず,正方形のグルーピングと順序付けアルゴリズムは失敗するでしょう).
cv::solvePnP¶
- void solvePnP(const Mat& objectPoints, const Mat& imagePoints, const Mat& cameraMatrix, const Mat& distCoeffs, Mat& rvec, Mat& tvec, bool useExtrinsicGuess=false)¶
3次元-2次元の対応点から,物体の姿勢を求めます.
パラメタ: - objectPoints – 物体座標空間における物体上の点座標の配列.3xN または Nx3 のシングルチャンネル配列,あるいは 1xN または Nx1 の3チャンネル配列.ここで N は点の個数を表します. ここでは vector<Point3f> を渡すこともできます
- imagePoints – 画像上の対応点の配列.2xN または Nx2 のシングルチャンネル配列,あるいは 1xN または Nx1 の2チャンネル配列.ここで N は点の個数を表します. ここでは vector<Point2f> を渡すこともできます
- cameraMatrix – 入力されるカメラ行列
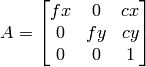
- distCoeffs – 入力される 4x1, 1x4, 5x1 または 1x5 の歪み係数ベクル
![(k_1, k_2, p_1, p_2[, k_3])](_images/math/00139c2d6590850e2b07264b39d783c0839b7337.png) . これが NULL の場合は,すべての歪み係数が0にセットされます
. これが NULL の場合は,すべての歪み係数が0にセットされます - rvec – 出力される回転ベクトル( Rodrigues2 を参照してください).( tvec とともに用いることで)点をモデル座標系からカメラ座標系に移動します
- tvec – 出力される並進ベクトル
- useExtrinsicGuess – これが真(1)の場合,この関数は,与えられた rvec と tvec を,それぞれ回転ベクトルと並進ベクトルの初期近似値として利用し,それらを最適化します
この関数は,カメラ行列や歪み係数と共に,物体上の点座標とそれに対応する画像上の投影点の集合が与えられた場合に,物体の姿勢を推定します.そのような姿勢は,再投影誤差を最小にするように求められます.つまり,観測された投影点 imagePoints と( ProjectPoints2 を用いて) objectPoints を投影した点との距離の2乗和を最小にします.
cv::findFundamentalMat¶
- Mat findFundamentalMat(const Mat& points1, const Mat& points2, vector<uchar>& status, int method=FM_RANSAC, double param1=3., double param2=0.99)¶
- Mat findFundamentalMat(const Mat& points1, const Mat& points2, int method=FM_RANSAC, double param1=3., double param2=0.99)
2つの画像の対応点からF行列を求めます.
パラメタ: - points1 – 1番目の画像中の N 個の点の配列. .点座標は,浮動小数点型(単精度または倍精度)です
- points2 – 2番目の画像中対応点の配列. points1 と同じサイズ,同じフォーマット
- method –
F行列を計算する手法
- CV_FM_7POINT 7-point アルゴリズム.
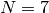
- CV_FM_8POINT 8-point アルゴリズム.
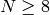
- CV_FM_RANSAC RANSAC アルゴリズム.
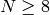
- CV_FM_LMEDS LMedS アルゴリズム.
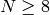
- CV_FM_7POINT 7-point アルゴリズム.
- param1 – RANSAC の場合のみ利用されるパラメータ.点からエピポーラ線までの最大距離をピクセル単位で表します.その距離を超えるものは外れ値であると判断され,最終的なF行列の計算に使用されません.点座標の精度,画像の解像度,画像のノイズなどに依存して,1-3程度の値にセットされます
- param2 – RANSAC または LMedS の場合にのみ使用されるパラメータ.推定されるF行列がどれほど正しいかを示す信頼(確率)値の要求値を表します
- status – N要素の出力配列.各要素は対応する点が外れ値ならば0にセットされ,そうでなければ1にセットされます.この配列は, RANSAC または LMedS の場合のみ計算されます.その他の手法の場合は,すべて1にセットされます
エピポーラ幾何は,次の式で説明されます:
![[p_2; 1]^T F [p_1; 1] = 0](_images/math/0ba9438e14e73a4bac80f18d7aa26cb1c2531543.png)
ここで,
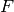 はF行列,
はF行列,
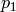 と
と
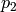 はそれぞれ,1番目と2番目の画像での対応点を表します.
はそれぞれ,1番目と2番目の画像での対応点を表します.
この関数は,上述の4つの手法の内の1つを用いてF行列を計算し,
求められたF行列
を返します.
通常,行列は1つだけ求められますが,7-point アルゴリズムを利用する場合,この関数は3つまでの解(すべての行列を順番に格納した
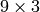 の行列)を返すことがあります
の行列)を返すことがあります
計算されたF行列はさらに,指定された点に対応するエピポーラ線を求める関数 ComputeCorrespondEpilines に渡される場合があります.また,平行化変換を求めるために StereoRectifyUncalibrated に渡すこともできます.
// 例.RANSAC アルゴリズムを用いた F 行列の推定
int point_count = 100;
vector<Point2f> points1(point_count);
vector<Point2f> points2(point_count);
// ここで点を初期化します ...
for( int i = 0; i < point_count; i++ )
{
points1[i] = ...;
points2[i] = ...;
}
Mat fundamental_matrix =
findFundamentalMat(points1, points2, FM_RANSAC, 3, 0.99);
cv::findHomography¶
- Mat findHomography(const Mat& srcPoints, const Mat& dstPoints, Mat& status, int method=0, double ransacReprojThreshold=0)¶
- Mat findHomography(const Mat& srcPoints, const Mat& dstPoints, vector<uchar>& status, int method=0, double ransacReprojThreshold=0)
- Mat findHomography(const Mat& srcPoints, const Mat& dstPoints, int method=0, double ransacReprojThreshold=0)
2つの画像間の透視変換を求めます.
パラメタ: - srcPoints – 元平面の点群の座標. CV_32FC2 型の行列,あるいは vector<Point2f>
- dstPoints – 目的平面の点群の座標. CV_32FC2 型の行列,あるいは vector<Point2f>
- method –
ホモグラフィ行列を求めるための手法:以下の内の1つ:
- 0 全ての点の組を利用する通常の手法
- CV_RANSAC RANSACアルゴリズムに基づくロバストな手法
- CV_LMEDS LMedS推定(Least-Median)によるロバストな手法
- ransacReprojThreshold –
点の組を,インライア値(外れ値ではないもの)として扱うために許容される逆投影誤差の最大値(これは,RANSACメソッドでのみ利用されます).つまり,もし
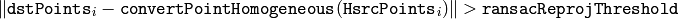
であれば,点
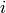 は外れ値であるとみなされます. srcPoints と dstPoints がピクセル単位で表されているならば,このパラメータは1から10の範囲内の値が妥当です
は外れ値であるとみなされます. srcPoints と dstPoints がピクセル単位で表されているならば,このパラメータは1から10の範囲内の値が妥当です - status – ロバスト手法( CV_RANSAC または CV_LMEDS )を利用した場合に,オプションとして出力されるマスク. 入力マスク値は無視されることに注意してください
これらの関数
は,元平面と目的平面との間の透視変換
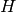 を求め
,それを返し
ます:
を求め
,それを返し
ます:
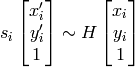
つまり,以下の逆投影誤差を最小化します.
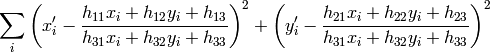
パラメータ method がデフォルト値の 0 にセットされた場合,この関数はすべての点の組を利用して,単純な最小二乗法によりホモグラフィ行列を推定します.
しかし,透視投影変換ですべての点の組(
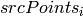 ,
,
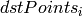 )を一致させることができない(つまり,外れ値がある)場合でも,ロバストな手法を選択することで正しい変換を推定することができます.
RANSAC
と
LMedS
のどちらの手法も,対応する点の組のランダムな部分集合(各4組)を繰り返し生成し,この部分集合と単純な最小二乗法を用いてホモグラフィ行列を推定します.そして,求められたホモグラフィ行列の質/状態(RANSACの場合はインライアの数,LMedS推定の場合は中央値の逆投影誤差)を計算します.
この最適な部分集合から,ホモグラフィ行列の初期推定値とインライア/アウトライアのマスクが生成されます.
)を一致させることができない(つまり,外れ値がある)場合でも,ロバストな手法を選択することで正しい変換を推定することができます.
RANSAC
と
LMedS
のどちらの手法も,対応する点の組のランダムな部分集合(各4組)を繰り返し生成し,この部分集合と単純な最小二乗法を用いてホモグラフィ行列を推定します.そして,求められたホモグラフィ行列の質/状態(RANSACの場合はインライアの数,LMedS推定の場合は中央値の逆投影誤差)を計算します.
この最適な部分集合から,ホモグラフィ行列の初期推定値とインライア/アウトライアのマスクが生成されます.
手法がロバストかどうかにかかわらず,求められたホモグラフィ行列は,逆投影誤差がより小さくなるように,Levenberg-Marquardt 法を用いてさらに(ロバスト推定の場合はインライア値のみを利用して)高精度化されます.
RANSAC を指定すると,実際にはどれだけアウトライアが混ざったデータも扱うことができますが,インライアとアウトライアを区別するための閾値が必要となります. LMedS を指定すると,この様な閾値は必要なくなりますが,データの50 % 以上がインライアでなければ正しく動作しません. また,計算された特徴点列内存在するノイズが僅かであり,アウトライアがないことが分かっている場合は,デフォルトの手法が最も良い選択です.
%– correctly only when there are more than 50 % of inliers. Finally,
この関数は,内部および外部パラメータ行列の初期推定値を求めるために利用されます.
ホモグラフィ行列は,スケールに依存するので,
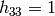 となるように正規化されます.
となるように正規化されます.
参考: GetAffineTransform , GetPerspectiveTransform , EstimateRigidMotion , WarpPerspective , PerspectiveTransform
cv::getDefaultNewCameraMatrix¶
- Mat getDefaultNewCameraMatrix(const Mat& cameraMatrix, Size imgSize=Size(), bool centerPrincipalPoint=false)¶
デフォルトの新たなカメラ行列を返します.
パラメタ: - cameraMatrix – 入力されるカメラ行列
- imageSize – ピクセル単位で表される,カメラビューの画像サイズ
- centerPrincipalPoint – 新たなカメラ行列において,主点が画像中心にあるかどうかを示します
この関数は,カメラ行列,つまり入力された cameraMatrix の完全なコピー( centerPrinicipalPoint=false の場合),またはそれを修正したもの( centerPrincipalPoint=true の場合),を返します.
後者の場合,新たなカメラ行列は次のようになります:

ここで
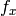 と
と
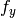 はそれぞれ,
cameraMatrix
における
はそれぞれ,
cameraMatrix
における
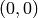 と
と
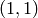 の要素になります.
の要素になります.
デフォルトでは,OpenCVの歪み補正関数( initUndistortRectifyMap , undistort を参照してください)は,主点を動かしません.しかし,ステレオカメラを利用する場合,両方のビューが同じy-座標を持つように(これは,大部分のステレオ対応点探索アルゴリズムで要求されます),主点を動かすことが重要です.この際に,x-座標も同じになる可能性があります.こうして,各ビューに対する新たなカメラ行列を作ることができます.この場合の主点は,それぞれのビューの中心にあります.
cv::getOptimalNewCameraMatrix¶
- Mat getOptimalNewCameraMatrix(const Mat& cameraMatrix, const Mat& distCoeffs, Size imageSize, double alpha, Size newImageSize=Size(), Rect* validPixROI=0)¶
フリースケーリングパラメータに基づいて,新たなカメラ行列を返します
パラメタ: - cameraMatrix – 入力されるカメラ行列
- distCoeffs – 入力される 4x1, 1x4, 5x1 または 1x5 の歪み係数ベクトル
![(k_1, k_2, p_1, p_2[, k_3])](_images/math/00139c2d6590850e2b07264b39d783c0839b7337.png)
- imageSize – 最適画像サイズ
- alpha – フリースケーリングパラメータ.0(歪み補正された画像のすべてのピクセルが有効)から1(歪み補正された画像においても,元画像のすべてのピクセルを保持)の間の値をとります. StereoRectify を参照してください
- newCameraMatrix – 出力される新たなカメラ行列
- newImageSize – 平行化された後の画像サイズ.デフォルトでは imageSize にセットされます
- validPixROI – オプション出力.歪み補正された画像中のすべての有効なピクセル領域を囲む矩形. StereoRectify の roi1, roi2 の説明を参照してください
この関数は,フリースケーリングパラメータに基づいて,最適な新しいカメラ行列を求め ,それを返し ます.このパラメータを変化させることで,ユーザは目的にあうピクセルだけを取り出したり alpha=0 ,コーナーを重要視して,すべての元画像ピクセルを保持したり alpha=1 ,あるいはその中間で,何か別のピクセルを得たりします.また, alpha>0 の場合,歪み補正された結果には,補正前の画像の外側にある「仮想」ピクセルに対応した黒いピクセルが含まれる可能性があります.元のカメラ行列,歪み係数,求められた新しいカメラ行列,そして newImageSize は, Remap 用のマップを生成するために InitUndistortRectifyMap に渡されるべきものです.
cv::initCameraMatrix2D¶
- Mat initCameraMatrix2D(const vector<vector<Point3f> >& objectPoints, const vector<vector<Point2f> >& imagePoints, Size imageSize, double aspectRatio=1.)¶
3次元-2次元の対応点から,カメラの内部パラメータ行列を求めます.
パラメタ: - objectPoints – 物体の点群のベクトルのベクトル. calibrateCamera() を参照してください
- imagePoints – 対応する画像点のベクトルのベクトル. calibrateCamera() を参照してください
- imageSize – ピクセル単位で表された画像サイズ.主点を初期化するために利用されます
- aspectRatio – これが0以下の場合,
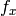 と
と 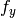 は独立に推定されます.そうでない場合,
は独立に推定されます.そうでない場合, 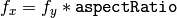 となります
となります
この関数は,キャリブレーション処理のためのカメラ行列の初期値を推定します.
現在のところ,平面のキャリブレーション器具,つまり,物体上の点の z-座標=0 となるようなもののみをサポートします.
cv::initUndistortRectifyMap¶
- void initUndistortRectifyMap(const Mat& cameraMatrix, const Mat& distCoeffs, const Mat& R, const Mat& newCameraMatrix, Size size, int m1type, Mat& map1, Mat& map2)¶
歪み補正および平行化変換のマップを求めます.
パラメタ: - cameraMatrix – 入力されるカメラ行列
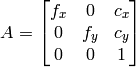
- distCoeffs – 入力される 4x1, 1x4, 5x1 または 1x5 の歪み係数ベクトル
![(k_1, k_2, p_1, p_2[, k_3])](_images/math/00139c2d6590850e2b07264b39d783c0839b7337.png)
- R – オプション.物体空間における平行化変換(3x3 の行列).ここでは StereoRectify によって求められた R1 または R2 を渡すことができます.この行列が empty だった場合,恒等変換が仮定されます
- newCameraMatrix – 新しいカメラ行列
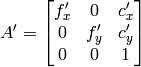
- size – 歪み補整された画像サイズ
- m1type – 1番目の出力マップの型. CV_32FC1 または CV_16SC2 のいずれか. convertMaps() を参照してください
- map1 – 1番目の出力マップ.
- map2 – 2番目の出力マップ.
- cameraMatrix – 入力されるカメラ行列
この関数は,歪み補正変換と平行化変換を結合させた変換を求め,その結果を Remap 用のマップの形式で表現します.歪み補整された画像は,まるで,カメラ行列が =newCameraMatrix で歪みを持たないカメラで撮影したかのような画像に見えます.単眼カメラの場合,通常, newCameraMatrix は cameraMatrix と等しくなるか,あるいはスケーリングを制御する必要があれば GetOptimalNewCameraMatrix によって求められます.ステレオカメラの場合,通常, newCameraMatrix は StereoRectify によって求められた P1 または P2 にセットされます.
また,この新しいカメラは, R に従って,個別に座標空間内での方向が決められます.これにより,例えば,ステレオカメラの両方の画像のエピポーラ線が平行で,同じy-座標を持つように各カメラを揃えることができるようになります (これは,横に並んだステレオカメラの場合です).
この関数は,実際に
Remap
で利用される逆マッピングアルゴリズム用のマップを生成ます.すなわち,この関数は,(歪み補正,平行化された)出力画像の各ピクセル
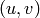 毎に,それに対応する元画像(つまり,カメラからのオリジナル画像)の座標を求めます.その処理は,以下のようになります:
毎に,それに対応する元画像(つまり,カメラからのオリジナル画像)の座標を求めます.その処理は,以下のようになります:
![\begin{array}{l} x \leftarrow (u - {c'}_x)/{f'}_x \\ y \leftarrow (v - {c'}_y)/{f'}_y \\{[X\,Y\,W]} ^T \leftarrow R^{-1}*[x \, y \, 1]^T \\ x' \leftarrow X/W \\ y' \leftarrow Y/W \\ x" \leftarrow x' (1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + 2p_1 x' y' + p_2(r^2 + 2 x'^2) \\ y" \leftarrow y' (1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + p_1 (r^2 + 2 y'^2) + 2 p_2 x' y' \\ map_x(u,v) \leftarrow x" f_x + c_x \\ map_y(u,v) \leftarrow y" f_y + c_y \end{array}](_images/math/b2ef04e09ac8e397d10674839524575bbc2ffb3e.png)
ここで
![(k_1, k_2, p_1, p_2[, k_3])](_images/math/00139c2d6590850e2b07264b39d783c0839b7337.png) は,歪み係数を表します.
は,歪み係数を表します.
ステレオカメラの場合,この関数は,各カメラ毎に1度ずつ,2度呼ばれます. StereoCalibrate の後 StereoRectify が呼ばれ,そしてこの関数が呼び出されます.しかし,ステレオカメラがキャリブレーションされていなかった場合でも, StereoRectifyUncalibrated を用いてF行列から直接,平行化変換を求めることが可能です.この関数は,各カメラに対して,3次元空間における回転行列 R ではなく,ピクセル領域における平行化変換として,ホモグラフィ行列 H を求めます. R は, H から次のようにして求めることができます:
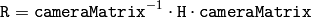
ここで cameraMatrix は,任意に選ぶことができます.
cv::matMulDeriv¶
- void matMulDeriv(const Mat& A, const Mat& B, Mat& dABdA, Mat& dABdB)¶
ある行列積を,それぞれの行列に関して偏微分します.
パラメタ: - A – 1番目の行列
- B – 2番目の行列
- dABdA – 1番目の出力.サイズ
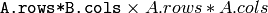 の偏微分行列 d(A*B)/dA
の偏微分行列 d(A*B)/dA - dABdB – 2番目の出力.サイズ
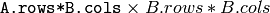 の偏微分行列 d(A*B)/dB
の偏微分行列 d(A*B)/dB
この関数は,行列積
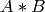 の要素を,2つの入力行列それぞれの要素に関して偏微分します.これは,
stereoCalibrate()
でヤコビ行列を求めるために利用されますが,その他の同様の最適化関数でも利用できます.
の要素を,2つの入力行列それぞれの要素に関して偏微分します.これは,
stereoCalibrate()
でヤコビ行列を求めるために利用されますが,その他の同様の最適化関数でも利用できます.
cv::projectPoints¶
- void projectPoints(const Mat& objectPoints, const Mat& rvec, const Mat& tvec, const Mat& cameraMatrix, const Mat& distCoeffs, vector<Point2f>& imagePoints)¶
- void projectPoints(const Mat& objectPoints, const Mat& rvec, const Mat& tvec, const Mat& cameraMatrix, const Mat& distCoeffs, vector<Point2f>& imagePoints, Mat& dpdrot, Mat& dpdt, Mat& dpdf, Mat& dpdc, Mat& dpddist, double aspectRatio=0)
3次元点を画像平面に投影します.
パラメタ: - objectPoints – 3次元物体上の点群座標の入力配列.これは,3xN または Nx3 のシングルチャンネル配列,あるいは 1xN または Nx1 の3チャンネル配列 (あるいは vector<Point3f> ) です.ここで N はビューの点の個数
- rvec – 回転ベクトル. Rodrigues2 を参照してください
- tvec – 並進ベクトル
- cameraMatrix – カメラ行列
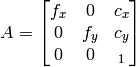
- distCoeffs – 入力 4x1, 1x4, 5x1 または 1x5 の歪み係数ベクトル
![(k_1, k_2, p_1, p_2[, k_3])](_images/math/00139c2d6590850e2b07264b39d783c0839b7337.png) .これが empty の場合,すべての歪み係数が0とみなされる
.これが empty の場合,すべての歪み係数が0とみなされる - imagePoints – 出力される,画像上の点の 2xN または Nx2 の1チャンネル配列,あるいは 1xN または Nx1 の2チャンネル配列. (あるいは vector<Point2f> )
- dpdrot – オプション.画像点を回転ベクトルの各要素に関して微分した 2Nx3 の行列
- dpdt – オプション.画像点を並進ベクトルの各要素に関して微分した 2Nx3 の行列
- dpdf – オプション.画像点を
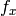 と
と 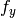 に関して微分した 2Nx2 の行列
に関して微分した 2Nx2 の行列 - dpdc – オプション.画像点を
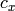 と
と 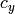 に関して微分した 2Nx2 の行列
に関して微分した 2Nx2 の行列 - dpddist – オプション.画像点を各歪み係数に関して微分した 2Nx4 の行列
この関数は,カメラの内部・外部パラメータが与えられると,3次元点を画像平面に投影します. オプションとして,この関数はヤコビ行列,つまり画像点を入力パラメータすべての関数とみなし,特定のカメラパラメータ,内部および/または外部パラメータで偏微分した行列,を求めます. 求められたヤコビ行列は, CalibrateCamera2 , FindExtrinsicCameraParams2 そして StereoCalibrate での大域的最適化において利用されます.この関数自身も,現在の内部・外部パラメータが与えられた場合の再投影誤差を求めるために利用されます.
rvec=tvec=(0,0,0) ,または 3x3 の単位行列にするために distCoeffs=Mat() とセットすることによって,この関数を利用した様々な部分事例を得ることができることに注意してください.つまり,疎な点集合に対する歪んだ座標を求めたり,歪みのない理想的なものとして透視変換を適用したり(そして,その微分を求めたりも)できます.
cv::reprojectImageTo3D¶
- void reprojectImageTo3D(const Mat& disparity, Mat& _3dImage, const Mat& Q, bool handleMissingValues=false)¶
視差画像を3次元空間に再投影します.
パラメタ: - disparity – 入力される,シングルチャンネル,16ビット符号付き,または32ビット浮動小数点型の視差画像
- _3dImage – 出力される,3チャンネルで disparity と同じサイズの浮動小数点型画像. _3dImage(x,y) の各要素は,視差マップから求められた点 (x,y) の3次元座標を含みます
- Q – StereoRectify によって得られる
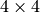 の透視変換行列
の透視変換行列 - handleMissingValues – これが真の場合,最小の視差を持つピクセル(これは外れ値に対応します. FindStereoCorrespondenceBM を参照してください)は,非常に大きいZの値(現在は 10000 にセットされています)を持つ3次元点に変換されます
この関数は,1チャンネルの視差マップを,3次元面を表現する3チャンネルの画像に変換します.つまり,各ピクセル (x,y) と,それに対応する視差 d=disparity(x,y) に対して,次のように計算されます:
![\begin{array}{l} [X \; Y \; Z \; W]^T = \texttt{Q} *[x \; y \; \texttt{disparity} (x,y) \; 1]^T \\ \texttt{\_3dImage} (x,y) = (X/W, \; Y/W, \; Z/W) \end{array}](_images/math/1af29654ff7bcec951f0d0adb80aadf62672fde5.png)
行列
Q
は,例えば,
StereoRectify
によって求められるような任意の
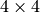 行列です.疎な点集合 {(x,y,d),...} を3次元空間に再投影するためには,
PerspectiveTransform
を利用します.
行列です.疎な点集合 {(x,y,d),...} を3次元空間に再投影するためには,
PerspectiveTransform
を利用します.
cv::RQDecomp3x3¶
- Vec3d RQDecomp3x3(const Mat& M, Mat& R, Mat& Q, Mat& Qx, Mat& Qy, Mat& Qz)
3x3 行列の ‘RQ’ 分解を行います.
パラメタ: - M – 入力される
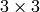 の浮動小数点型行列
の浮動小数点型行列 - R – 出力される
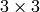 の上三角行列
の上三角行列 - Q – 出力される
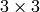 の直行行列
の直行行列 - Qx – オプション.x-軸周りの 3x3 の回転行列
- Qy – オプション.y-軸周りの 3x3 の回転行列
- Qz – オプション.z-軸周りの 3x3 の回転行列
- M – 入力される
この関数は,ギブンス回転を利用して RQ 分解を行います.これは, DecomposeProjectionMatrix において,射影行列の左 3x3 部分行列を,カメラ行列と回転行列に分解するために利用されます.
またオプションとして,各軸周りの3つの回転行列,そしてOpenGLで利用できる3つのオイラー角を (戻り値として) 得ることができます.
cv::Rodrigues¶
- void Rodrigues(const Mat& src, Mat& dst, Mat& jacobian)
回転行列と回転ベクトルを相互に変換します.
パラメタ: - src – 入力回転ベクトル(3x1 または 1x3),または入力回転行列(3x3)
- dst – 出力回転行列(3x3),または出力回転ベクトル(3x1 または 1x3)
- jacobian – オプションとして出力される, 3x9 または 9x3 のヤコビ行列.出力配列要素を入力配列要素で偏微分したものです
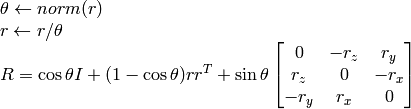
以下の関係から,逆変換も簡単に行うことができます.
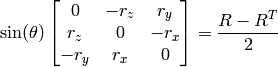
回転ベクトルは,便利で最もコンパクトな回転行列の表現方法です(すべての回転行列は丁度3自由度なので). この表現方法は, CalibrateCamera2 , StereoCalibrate または FindExtrinsicCameraParams2 のような3次元幾何学の大域的最適化処理において利用されます.
StereoBM¶
- StereoBM¶
ブロックマッチングアルゴリズムを利用したステレオ対応点探索のためのクラス.
// ブロックマッチングステレオ対応点探索アルゴリズム
class StereoBM
{
enum { NORMALIZED_RESPONSE = CV_STEREO_BM_NORMALIZED_RESPONSE,
BASIC_PRESET=CV_STEREO_BM_BASIC,
FISH_EYE_PRESET=CV_STEREO_BM_FISH_EYE,
NARROW_PRESET=CV_STEREO_BM_NARROW };
StereoBM();
// この preset は,上述の _PRESET の 1 つ.
// ndisparities は,各ピクセルにおける
// 最適な視差の探索範囲となる視差サイズ.
// SADWindowSize は,ピクセルブロックマッチに利用される平均化窓のサイズ.
// (値が大きくなるとノイズに対して頑健になりますが,ボケた視差マップが生成されます)
StereoBM(int preset, int ndisparities=0, int SADWindowSize=21);
// 単独の初期化関数
void init(int preset, int ndisparities=0, int SADWindowSize=21);
// 2 つの平行化された 8 ビット,シングルチャンネル画像に対する視差を求めます.
// この視差画像は left と同じサイズの, 16 ビット符号あり(固定小数点型),または 32 ビット浮動小数点型の画像です.
void operator()( const Mat& left, const Mat& right, Mat& disparity, int disptype=CV_16S );
Ptr<CvStereoBMState> state;
};
このクラスは, とそれに関連する関数の,C++ ラッパーです.具体的に言えば, FindStereoCorrespondceBM のラッパーは StereoBM::operator () になります.それぞれの説明を参照してください.
StereoSGBM¶
- StereoSGBM¶
セミグローバルブロックマッチングアルゴリズムを用てステレオ対応点探索を行うためのクラス
class StereoSGBM
{
StereoSGBM();
StereoSGBM(int minDisparity, int numDisparities, int SADWindowSize,
int P1=0, int P2=0, int disp12MaxDiff=0,
int preFilterCap=0, int uniquenessRatio=0,
int speckleWindowSize=0, int speckleRange=0,
bool fullDP=false);
virtual ~StereoSGBM();
virtual void operator()(const Mat& left, const Mat& right, Mat& disp);
int minDisparity;
int numberOfDisparities;
int SADWindowSize;
int preFilterCap;
int uniquenessRatio;
int P1, P2;
int speckleWindowSize;
int speckleRange;
int disp12MaxDiff;
bool fullDP;
...
};
このクラスは, H. Hirschmuller のアルゴリズム HH08 を元に実装されています.これと元のアルゴリズムとの主な違いは以下のとおりです:
- デフォルトでは,このアルゴリズムは 1 パスです.つまり,8方向ではなく5方向しか考慮されません.このアルゴリズムの完全版( 大量の メモリを消費する場合があります)を実行するには, fullDP=true としてください.
- このアルゴリズムは,個々のピクセル同士ではなくブロック同士を比較します(が, SADWindowSize=1 とすると,1ブロックが1ピクセルとなります).
- 相互情報量コスト関数は実装されていません.その代わり,より単純な Birchfield-Tomasi サブピクセル基準 BT96 を利用しています.また,カラー画像も同様にサポートしています.
- K. Konolige アルゴリズム FindStereoCorrespondceBM から,いくつかの事前,事後処理ステップを組み込みました.これは,事前フィルタリング( CV_STEREO_BM_XSOBEL )や事後フィルタリング( 一意性チェック,二次補間,スペックルフィルタリング)などです.
cv::StereoSGBM::StereoSGBM¶
- StereoSGBM::StereoSGBM()¶
- StereoSGBM::StereoSGBM(int minDisparity, int numDisparities, int SADWindowSize, int P1=0, int P2=0, int disp12MaxDiff=0, int preFilterCap=0, int uniquenessRatio=0, int speckleWindowSize=0, int speckleRange=0, bool fullDP=false)
StereoSGBM コンストラクタ
パラメタ: - minDisparity – 取り得る最小の視差値.通常は0ですが,平行化のアルゴリズムによって画像が移動する場合があるので,それに応じてこのパラメータを調整する必要があります
- numDisparities – 取り得る最大の視差値.常に0より大きい値となります.現在の実装では,この値は16の倍数でなければいけません
- SADWindowSize – マッチングされるブロックのサイズ.必ず奇数 >=1 となります.通常は, 3..11 の範囲内の値になります
- P1, P2 – 視差のなめらかさを制御するパラメータ.この値が大きくなると,視差がなめらかになります. P1 は,隣り合うピクセル間で視差が +1 または -1 変化した場合のペナルティです.また, P2 は,隣り合うピクセル間で視差が 1 よりも大きく 変化した場合のペナルティです.このアルゴリズムでは, P2 > P2 でなければいけません.妥当な P1 と P2 の値(それぞれ, 8*number_of_image_channels*SADWindowSize*SADWindowSize と 32*number_of_image_channels*SADWindowSize*SADWindowSize )が書かれている stereo_match.cpp のサンプルを参照してください
- disp12MaxDiff – left-right 視差チェックにおけて許容される最大の差(整数のピクセル単位).チェックを行わない場合は,これを 0 または負の値にしてください
- preFilterCap – 事前フィルタにおいて,画像ピクセルを切り捨てる閾値.このアルゴリズムは,まず,各ピクセルのx-微分を求め,その値を [-preFilterCap, preFilterCap] 区間で切り取ります.そして,その結果が Birchfield-Tomasi コスト関数に渡されます
- uniquenessRatio – パーセント単位で表現されるマージン.正しい値を求めるため,求められた最適な(最小の)コスト関数値は,このマージン以上の差で2番目に最適な値に「勝つ」必要があります
- speckleWindowSize – ノイズスペックルや無効なピクセルが考慮されたなめらかな視差領域の最大サイズ.スペックルフィルタを無効にする場合は,これを0にセットしてください.そうでない場合は,50-200 の範囲内の値にします
- speckleRange – それぞれの連結成分における最大視差値.スペックルフィルタリングを行う場合,これは正の値で16の倍数にしてください.通常は,16 または 32 が適切な値です
- fullDP – 完全な 2 パス,動的計画法のアルゴリズムを動作させるには,これを true にします.このアルゴリズムは, O(W*H*numDisparities) バイトのメモリを消費します.これは,640x480 のステレオに対しても大きな値で,HD-サイズの画像の場合は莫大な値になります.デフォルトでは,これは false です
1番目のコンストラクタは,デフォルトパラメータで StereoSGBM を初期化します(実際は,少なくとも StereoSGBM::numberOfDisparities だけは設定する必要があります).2番目のコンストラクタは,各パラメータに好きなパラメータをセットすることができます.
cv::StereoSGBM::operator ()¶
- void SGBM::operator()(const Mat& left, const Mat& right, Mat& disp)¶
平行化されたステレオペアに対して,SGBM アルゴリズムを用いて視差を求めます.
パラメタ: - left – 左画像.8-ビット,シングルチャンネルまたは3チャンネル
- right – 右画像.左画像と同じサイズ,同じ型
- disp – 出力される視差画像.入力画像と同じサイズで,16-ビット,符号ありのシングルチャンネル画像です.これには,16倍された視差値が保存されています.つまり,浮動小数点型の視差マップを得るには, disp の要素を16で割る必要があります
このメソッドは,平行化されたステレオペアに対して,SGBM アルゴリズムを実行します.画像の準備やメソッドの呼び出し方については,OpenCVの stereo_match.cpp サンプルを参照してください.このメソッドは constant ではないので,同一の StereoSGBM インスタンスを,複数のスレッドから同時に利用するべきではないことに注意してください.
cv::stereoCalibrate¶
- double stereoCalibrate(const vector<vector<Point3f> >& objectPoints, const vector<vector<Point2f> >& imagePoints1, const vector<vector<Point2f> >& imagePoints2, Mat& cameraMatrix1, Mat& distCoeffs1, Mat& cameraMatrix2, Mat& distCoeffs2, Size imageSize, Mat& R, Mat& T, Mat& E, Mat& F, TermCriteria term_crit = TermCriteria(TermCriteria::COUNT+ TermCriteria::EPS, 30, 1e-6), int flags=CALIB_FIX_INTRINSIC)¶
ステレオカメラのキャリブレーションを行います.
パラメタ: - objectPoints – キャリブレーションパターン上の点群座標(座標系はパターンに固定)を表すベクトル,のベクトル.1つのビュー毎に1つのベクトルがあります.同じキャリブレーションパターンがそれぞれのビューに完全に写っている場合,その座標ベクトルはすべて同じにできます.しかし,部分的に隠れたパターンや,異なるビューに別のパターンが写っている場合などは,そのベクトルは別の値になります.点群は3次元ですが,それらはパターン座標形上にあるので,この器具が平面ならば,器具平面とXY 座標平面とを一致させて点群の Z-座標が0になるようにするのは適切なやり方と言えます
- imagePoints1 – 物体(キャリブレーションパターン)上の点群を1番目のカメラのビューに投影した点群座標のベクトル,のベクトル.1つのビュー毎に1つのベクトルがあります.投影点は,対応する物体上の点群と同じ順序でなければいけません
- imagePoints2 – 物体(キャリブレーションパターン)上の点群を2番目のカメラのビューに投影した点群座標のベクトル,のベクトル.1つのビュー毎に1つのベクトルがあります.投影点は,対応する物体上の点群と同じ順序でなければいけません
- cameraMatrix1 – 入出力.1番目のカメラ行列:
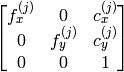 ,
, 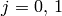 もし, CV_CALIB_USE_INTRINSIC_GUESS , CV_CALIB_FIX_ASPECT_RATIO , CV_CALIB_FIX_INTRINSIC あるいは CV_CALIB_FIX_FOCAL_LENGTH のいずれかが指定される場合は,いくつかの,あるいはすべての行列要素が初期化される必要があります.flags の説明を参照してください
もし, CV_CALIB_USE_INTRINSIC_GUESS , CV_CALIB_FIX_ASPECT_RATIO , CV_CALIB_FIX_INTRINSIC あるいは CV_CALIB_FIX_FOCAL_LENGTH のいずれかが指定される場合は,いくつかの,あるいはすべての行列要素が初期化される必要があります.flags の説明を参照してください - distCoeffs1 – 1番目のカメラに対するレンズ歪み係数.4x1, 5x1, 1x4 あるいは 1x5 の浮動小数点型ベクトル
![(k_1^{(j)}, k_2^{(j)}, p_1^{(j)}, p_2^{(j)}[, k_3^{(j)}])](_images/math/9341350d35c0b33716d8d9e4b5d811b700402f08.png) ,
, 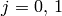 . CV_CALIB_FIX_K1 , CV_CALIB_FIX_K2 または CV_CALIB_FIX_K3 のいずれかが指定される場合,対応する歪み係数の要素は初期化されていなければいけません
. CV_CALIB_FIX_K1 , CV_CALIB_FIX_K2 または CV_CALIB_FIX_K3 のいずれかが指定される場合,対応する歪み係数の要素は初期化されていなければいけません - cameraMatrix2 – 入出力.2番目のカメラ行列.cameraMatrix1 と同様
- distCoeffs2 – 入出力.2番目のカメラに対するレンズ歪み係数.distCoeffs1 と同様
- imageSize – 画像サイズ.カメラの内部行列を初期化するためだけに利用されます
- R – 出力される,1番目と2番目のカメラ座標系間の回転行列
- T – 出力される,それぞれのカメラ座標系間の並進ベクトル
- E – 出力されるE行列
- F – 出力されるF行列
- term_crit – 反復最適化アルゴリズムの停止基準
- flags –
様々なフラグ.0または以下の値の組み合わせ:
- CV_CALIB_FIX_INTRINSIC これが指定された場合, distCoeffs? と同じく cameraMatrix? も固定され, R, T, E と F だけが推定されます
- CV_CALIB_USE_INTRINSIC_GUESS これが指定されると,いくつかの,またはすべての(これは他のフラグに依存します)内部パラメータが最適化されます.しかし,初期値はユーザが与える必要があります
- CV_CALIB_FIX_PRINCIPAL_POINT 最適化の間,主点が固定されます
- CV_CALIB_FIX_FOCAL_LENGTH
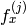 と
と 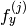 が固定されます
が固定されます - CV_CALIB_FIX_ASPECT_RATIO
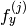 が最適化されますが,比率
が最適化されますが,比率 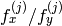 は固定されます
は固定されます - CV_CALIB_SAME_FOCAL_LENGTH 強制的に
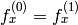 かつ
かつ 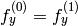 となります
となります - CV_CALIB_FIX_K1, CALIB_FIX_K2, CALIB_FIX_K3 対応する半径方向歪み係数が固定されます(その係数の値を関数に渡す必要があります)
この関数は,ステレオペアを構成する2つのカメラ間の変換を推定します.2つのカメラの相対位置と相対姿勢が固定されたステレオカメラがあり,1番目のカメラと2番目のカメラに対する物体の姿勢 (R1, T1) と (R2, T2) をそれぞれ計算したとすると,これらの姿勢は明らかに互いに関係があります.つまり, (
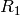 ,
,
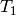 ) が与えられると, (
) が与えられると, (
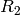 ,
,
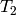 ) を求めることができるので,我々は,2番目のカメラの1番目のカメラに対する位置と姿勢さえ知っていればよいことになります.これが,この関数の働きです.これは (
) を求めることができるので,我々は,2番目のカメラの1番目のカメラに対する位置と姿勢さえ知っていればよいことになります.これが,この関数の働きです.これは (
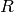 ,
,
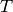 ) を次のように求めます:
) を次のように求めます:
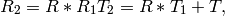
またオプションとして,E 行列を求めます.
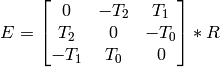
ここで
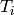 は,並進ベクトル
は,並進ベクトル
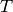 :
:
![T=[T_0, T_1, T_2]^T](_images/math/586c8ad76bed1689a0d7d3cf8356439559b1d4de.png) の要素を表します.さらに,この関数は F行列も求めることができます.
の要素を表します.さらに,この関数は F行列も求めることができます.
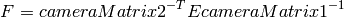
この関数は,ステレオカメラの位置姿勢関係を求めるだけでなく,2つのカメラそれぞれの完全なキャリブレーションも行うことができます.しかし,パラメータ空間の次元が大きすぎる事や,入力データのノイズなどが原因で,最適解を得られない可能性もあります.したがって,各カメラの内部パラメータを(例えば CalibrateCamera2 を用いて)個々に高精度に推定できるならば,そちらの方法が推奨されます.その後に,その計算された内部パラメターと CALIB_FIX_INTRINSIC フラグをこの関数に渡せばよいです.それが無理で,全てのパラメータを一度に計算する場合,いくつかのパラメータに制限を与えると良いでしょう.例えば, CV_CALIB_SAME_FOCAL_LENGTH フラグと CV_CALIB_ZERO_TANGENT_DIST フラグを指定することは,通常は妥当な仮定と言えます.
CalibrateCamera2 と同様に,この関数は,両方のカメラのすべてのビューのすべての点の再投影誤差の和を最小化します.
また,この関数は,最終的な再投影誤差を返します.
cv::stereoRectify¶
- void stereoRectify(const Mat& cameraMatrix1, const Mat& distCoeffs1, const Mat& cameraMatrix2, const Mat& distCoeffs2, Size imageSize, const Mat& R, const Mat& T, Mat& R1, Mat& R2, Mat& P1, Mat& P2, Mat& Q, int flags=CALIB_ZERO_DISPARITY)¶
- void stereoRectify(const Mat& cameraMatrix1, const Mat& distCoeffs1, const Mat& cameraMatrix2, const Mat& distCoeffs2, Size imageSize, const Mat& R, const Mat& T, Mat& R1, Mat& R2, Mat& P1, Mat& P2, Mat& Q, double alpha, Size newImageSize=Size(), Rect* roi1=0, Rect* roi2=0, int flags=CALIB_ZERO_DISPARITY)
キャリブレーション済みステレオの,それぞれのカメラの平行化変換を求めます.
パラメタ: - cameraMatrix1, cameraMatrix2 – カメラ行列
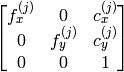 .
. - distCoeffs1, distCoeffs2 – 入力される,各カメラの歪み係数,
![{k_1}^{(j)}, {k_2}^{(j)}, {p_1}^{(j)}, {p_2}^{(j)} [, {k_3}^{(j)}]](_images/math/41ee0aa33912371d07818a29062d2d1acc24b645.png)
- imageSize – ステレオキャリブレーションに利用された画像サイズ
- R – 1番目と2番目のカメラの座標系間の回転行列
- T – 1番目と2番目のカメラの座標系間の並進ベクトル
- R1, R2 – 出力.それぞれ,1番目と2番目のカメラに対する
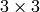 の平行化変換(回転行列)
の平行化変換(回転行列) - P1, P2 – 出力.新しい(平行化された)座標系における
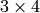 の射影行列
の射影行列 - Q – 出力.
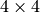 の視差-デプス間のマッピング行列. reprojectImageTo3D() を参照してください
の視差-デプス間のマッピング行列. reprojectImageTo3D() を参照してください - flags – 処理フラグ.0または CV_CALIB_ZERO_DISPARITY .このフラグがセットされている場合,関数は各カメラの主点を,平行化されたビューの同じピクセル座標にします.このフラグがセットされていない場合,関数は有効画像領域が最大になるように,画像を水平または垂直方向(これはエピポーラ線の方向に依存します)にずらす場合があります
- alpha – フリースケーリングパラメータ.これが -1 または未指定 の場合,関数はデフォルトのスケーリングを行います.そうでない場合,パラメータは0から1の間の値でなくてはいけません. alpha=0 は,有効なピクセルのみが見えるように,平行化された画像を拡大・並進することを意味します(つまり,平行化を行った後には黒い領域が残りません). alpha=1 は,カメラから得られた元画像のすべてのピクセルが平行化後の画像にも残っているように,平行化された画像を縮小・並進することを意味します(つまり,元画像のピクセルがまったく削除されません).もちろん,中間の値は,これらの対極のケースの中間の結果を生成します
- newImageSize – 平行化後の新しい画像の解像度.これと同じサイズが InitUndistortRectifyMap に渡されるべきです.OpenCV サンプルディレクトリの stereo_calib.cpp を参照してください.デフォルト,つまり (0, 0) が渡された場合は,これは元画像サイズ imageSize にセットされます.より大きな値をセットすると,大きな歪みがある場合は特に,元画像のディテールを保つことができるようになります
- roi1, roi2 – オプション出力.平行化された画像内の,すべてのピクセルが有効である領域を示す矩形. alpha=0 の場合,ROIは画像全体を含みます.そうでない場合,おそらく,よりも小さいサイズになるでしょう.以下の図を参照してください
- cameraMatrix1, cameraMatrix2 – カメラ行列
この関数は,各カメラの回転行列を求めます.この回転行列によって,両方のカメラの画像平面が(仮想的に)同一平面に乗るように変換されます.その結果,すべてのエピポーラ線が平行になるので,多数のステレオ対応点探索問題が単純化されます.この関数は, stereoCalibrate() によって求められた行列を入力にとり,2つの回転行列と,新しい座標系における2つの投影行列を出力します.この関数は,次の2つの場合を区別します:
- 水平ステレオ.1番目のカメラと2番目のカメラのビューが互いに,主に x 軸に沿った方向にずれている状態(多少は垂直方向の移動もあるかもしれません).
平行化された画像では,左右のカメラ間のエピポーラ線は,水平,かつ,同じ y-座標(高さ)になる.P1 と P2 は,以下のようになります:
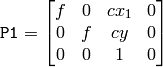
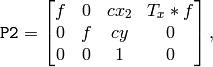
ここで,
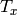 はカメラ間の水平方向のずれであり,
CV_CALIB_ZERO_DISPARITY
がセットされている場合は
はカメラ間の水平方向のずれであり,
CV_CALIB_ZERO_DISPARITY
がセットされている場合は
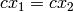 となります.
となります.- 垂直ステレオ.1番目のカメラと2番目のカメラのビューが互いに,主に y 軸に沿った方向にずれている状態(これも,多少は水平方向の移動があるかもしれません).
平行化された画像でのエピポーラ線は,垂直,かつ,同じ x-座標になる.P1 と P2 は,以下のようになります:
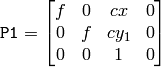
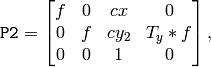
ここで,
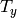 はカメラ間の垂直方向のずれであり,
CALIB_ZERO_DISPARITY
がセットされている場合は
はカメラ間の垂直方向のずれであり,
CALIB_ZERO_DISPARITY
がセットされている場合は
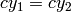 となります.
となります.
見ての通り, P1 と P2 の最初の3列は,「平行化された」新たなカメラ行列そのものです.
The matrices, together with R1 and R2 , can then be passed to InitUndistortRectifyMap to initialize the rectification map for each camera.
以下は, stereo_calib.cpp サンプルのスクリーンショットです.ここに示される赤い水平線は,対応する画像領域を通過しています.つまり,(多くのステレオ対応点探索アルゴリズムが前提とするように)両方の画像が綺麗に平行化されていることが分かります.また,緑の矩形は, roi1 と roi2 を示し,その中が確かにすべて有効なピクセルであることが分かります.

cv::stereoRectifyUncalibrated¶
- bool stereoRectifyUncalibrated(const Mat& points1, const Mat& points2, const Mat& F, Size imgSize, Mat& H1, Mat& H2, double threshold=5)¶
キャリブレーションされていないステレオの,それぞれのカメラの平行化変換を求めます.
パラメタ: - points1, points2 – 対応する2次元点を表すの2つの配列. FindFundamentalMat でサポートされるものと同じフォーマットです
- F – 入力されるF行列. FindFundamentalMat を利用して,これと同じ点ペアの集合から計算することができます
- imageSize – 画像サイズ
- H1, H2 – 出力される,1番目と2番目の画像に対する平行化ホモグラフィ行列
- threshold – 外れ値を除外するために用いられるオプションの閾値.このパラメータが0より大きい場合,ホモグラフィ行列を計算する前に,エピポーラ幾何に十分に従わない(つまり,
![|\texttt{points2[i]}^T*\texttt{F}*\texttt{points1[i]}|>\texttt{threshold}](_images/math/e77a03eb53f034dff5b0581485e41f7339b205bf.png) となる)すべての点ペアが棄却されます.そうでない場合,つまりパラメータが0以下の場合は,すべての点がインライアであると見なされます
となる)すべての点ペアが棄却されます.そうでない場合,つまりパラメータが0以下の場合は,すべての点がインライアであると見なされます
この関数は,カメラの内部パラメータや空間の相対的位置を必要とすることな く,平行化変換を求めます.なので,「Uncalibrated」という接尾辞がついています. StereoRectify とのもう一つの違いとして,関数の出力が,物体(3次元)空間における平行化変換ではなく,ホモグラフィ行列 H1 と H2 によってエンコードされた平面透視変換となることが挙げられます.この関数は,アルゴリズム Hartley99 の実装です.
このアルゴリズムは,カメラの内部パラメータを知る必要はありませんが,エピポーラ幾何に大きく依存していることに注意してください.したがって,カメラレンズが大きく歪んでいる場合は,F行列を計算してこの関数を呼び出すよりも前に,歪みを補正しておくのが賢明です.例えば,ステレオの各カメラの歪み係数は, CalibrateCamera2 を用いて個別に推定できます.画像は Undistort2 によって,点座標だけならば UndistortPoints によって補正することが可能です.
cv::undistort¶
- void undistort(const Mat& src, Mat& dst, const Mat& cameraMatrix, const Mat& distCoeffs, const Mat& newCameraMatrix=Mat())¶
レンズ歪みを補正するように画像を変形させます.
パラメタ: - src – (歪んだ)入力画像
- dst – (補正された)出力画像. src と同じサイズ,同じ型
- cameraMatrix – 入力されるカメラ行列
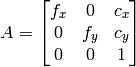
- distCoeffs – 歪み係数ベクトル,
![(k_1^{(j)}, k_2^{(j)}, p_1^{(j)}, p_2^{(j)}[, k_3^{(j)}])](_images/math/9341350d35c0b33716d8d9e4b5d811b700402f08.png)
- newCameraMatrix – 歪んだ画像のカメラ行列.デフォルトでは cameraMatrix と等しくなりますが,ユーザが別の行列を用いて結果にスケーリングや並進を加える可能性が考慮されています
この関数は,半径方向および円周方向のレンズ歪みを補正するように画像を変換します.
この関数は,単に InitUndistortRectifyMap ( R は単位行列)と Remap (バイリニア補間)を組み合わせたものです.変換の詳細については,前述の関数を参照してください.
元画像に対応するピクセルが存在しないような出力画像のピクセルは,0(黒色)で埋められます.
補正された画像内に残っている元画像の部分画像は newCameraMatrix で制御できます.ユーザは,必要に応じた適切な newCameraMatrix を求めるために GetOptimalNewCameraMatrix を利用することができます.
これらのカメラ行列と歪みパラメータは
CalibrateCamera2
を用いて決定できます.
画像の解像度がキャリブレーション時と異なる場合,歪み係数はそのままで構いませんが,
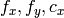 および
および
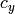 を適宜スケーリングする必要があります
を適宜スケーリングする必要があります
cv::undistortPoints¶
- void undistortPoints(const Mat& src, vector<Point2f>& dst, const Mat& cameraMatrix, const Mat& distCoeffs, const Mat& R=Mat(), const Mat& P=Mat())¶
- void undistortPoints(const Mat& src, Mat& dst, const Mat& cameraMatrix, const Mat& distCoeffs, const Mat& R=Mat(), const Mat& P=Mat())
観測された点座標から,理想的な点座標を求めます.
パラメタ: - src – 観測された点座標. ProjectPoints2 の imagePoints と同じフォーマット
- dst – 歪み補正および逆透視変換された後に出力される,理想的な点座標.
- cameraMatrix – カメラ行列
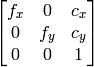
- distCoeffs – 歪み係数のベクトル
![(k_1^{(j)}, k_2^{(j)}, p_1^{(j)}, p_2^{(j)}[, k_3^{(j)}])](_images/math/9341350d35c0b33716d8d9e4b5d811b700402f08.png)
- R – 物体空間における平行化変換(3x3 の行列). StereoRectify() によって求められる R1 または R2 のどちらかが,ここに渡されます.この行列が空の場合,単位行列が変換行列として利用されます
- P – 新たなカメラ行列(3x3)または,新たな射影行列(3x4). StereoRectify() によって求められる P1 or P2 のどちらかが,ここに渡されます.この行列がemptyの場合,単位行列が新たなカメラ行列として利用されます
この関数は, Undistort2 や InitUndistortRectifyMap と似ていますが,ラスタ画像の代わりに,疎な点集合を扱います.また, ProjectPoints2 に対する逆変換のような処理も行います(3次元物体の場合は,当然その3次元座標を再構成するわけではありません.しかし,平面物体の場合は,適切な R が指定されれば,並進ベクトル次第で,そのようなことも起こります).
// (u,v) は入力点座標, (u', v') は出力点座標
// camera_matrix=[fx 0 cx; 0 fy cy; 0 0 1]
// P=[fx' 0 cx' tx; 0 fy' cy' ty; 0 0 1 tz]
x" = (u - cx)/fx
y" = (v - cy)/fy
(x',y') = undistort(x",y",dist_coeffs)
[X,Y,W]T = R*[x' y' 1]T
x = X/W, y = Y/W
u' = x*fx' + cx'
v' = y*fy' + cy',
ここで undistort() は,正規化された歪んだ点座標から,正規化されたオリジナルの点座標を推定する,反復近似アルゴリズムです(「正規化された」というのは,座標がカメラ行列に依存しないという意味です).
この関数は,ステレオの各カメラや単眼カメラに対して用いることができます(Rは empty ).
ヘルプとフィードバック
お探しの情報が見つかりませんか?- FAQ (英語)を試してください.
- ユーザグループ/メーリングリスト (英語)で質問してみてください.
- このドキュメントに誤りなどを見つけたらbug report まで報告してください.また,日本語訳に関する誤りや指摘はopencv.jpまでお願い します.
