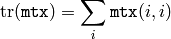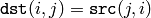配列操作¶
cv::abs¶
- MatExpr<...> abs(const MatExpr<...>& src)
各行列要素の絶対値を求めます.
Parameter: src – 行列または行列表現
abs はメタ関数であり, absdiff() の一形式に拡張されます:
- C = abs(A-B) は absdiff(A, B, C) と等価
- C = abs(A) は absdiff(A, Scalar::all(0), C) と等価
- C = Mat_<Vec<uchar, n > >(abs(A* alpha + beta)) は convertScaleAbs(A, C, alpha, beta) と等価
出力行列は,入力行列と同じサイズ同じ型(最後の場合を除きます.ここでは, C は depth=CV_8U となります).
参考: Matrix Expressions , absdiff() ,
cv::absdiff¶
- void absdiff(const MatND& src1, const MatND& src2, MatND& dst)
- void absdiff(const MatND& src1, const Scalar& sc, MatND& dst)
2つの配列同士,あるいは配列とスカラの 要素毎の差の絶対値を求めます.
パラメタ: - src1 – 1番目の入力配列
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- sc – 2番目の入力パラメータであるスカラ
- dst – src1 と同じサイズ,同じ型の出力配列. Mat::create を参照してください
関数 absdiff は,以下を求めます:
2つの配列の差の絶対値
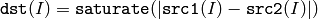
あるいは,配列とスカラの差の絶対値
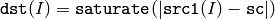
ここで I は,配列要素の多次元インデックスを表します.
マルチチャンネル配列の場合,各チャンネルは個別に処理されます.
参考: abs() ,
cv::add¶
- void add(const MatND& src1, const MatND& src2, MatND& dst)
- void add(const MatND& src1, const MatND& src2, MatND& dst, const MatND& mask)
- void add(const MatND& src1, const Scalar& sc, MatND& dst, const MatND& mask=MatND())
2つの配列同士,あるいは配列とスカラの 要素毎の和を求めます.
パラメタ: - src1 – 1番目の入力配列
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- sc – 2番目の入力パラメータであるスカラ
- dst – src1 と同じサイズ,同じ型の出力配列. Mat::create を参照してください
- mask – 8ビット,シングルチャンネル配列のオプションの処理マスク.出力配列内の変更される要素を表します
関数 add は,以下を求めます:
2つの配列の和:
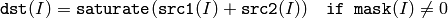
あるいは,配列とスカラの和
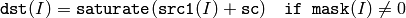
ここで I は,配列要素の多次元インデックスを表します.
上述のリストの最初の関数は,行列表現を用いて置き換えることができます:
dst = src1 + src2;
dst += src1; // add(dst, src1, dst); と等価
マルチチャンネル配列の場合,各チャンネルは個別に処理されます.
参考: subtract() , addWeighted() , scaleAdd() , convertScale() , Matrix Expressions , .
cv::addWeighted¶
- void addWeighted(const Mat& src1, double alpha, const Mat& src2, double beta, double gamma, Mat& dst)¶
- void addWeighted(const MatND& src1, double alpha, const MatND& src2, double beta, double gamma, MatND& dst)
2つの配列の重み付き和を求めます.
パラメタ: - src1 – 1番目の入力配列
- alpha – 1番目の配列要素に対する重み
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- beta – 2番目の配列要素に対する重み
- dst – src1 と同じサイズ,同じ型の出力配列
- gamma – スカラ,それぞれの和に加えられます
関数 addWeighted は,2つの配列の重み付き和を次のように求めます:
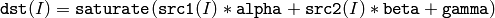
ここで I は,配列要素の多次元インデックスを表します.
最初の関数は,行列表現を用いてで置き換えることができます:
dst = src1*alpha + src2*beta + gamma;
マルチチャンネル配列の場合,各チャンネルは個別に処理されます.
参考: add() , subtract() , scaleAdd() , convertScale() , Matrix Expressions , .
cv::bitwise_and¶
- void bitwise_and(const MatND& src1, const MatND& src2, MatND& dst, const MatND& mask=MatND())
- void bitwise_and(const MatND& src1, const Scalar& sc, MatND& dst, const MatND& mask=MatND())
2つの配列同士,あるいは配列とスカラの ビット毎の論理積を求めます.
パラメタ: - src1 – 1番目の入力配列
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- sc – 2番目の入力パラメータであるスカラ
- dst – src1 と同じサイズ,同じ型になる出力配列. Mat::create を参照してください
- mask – 8ビットのシングルチャンネル配列であるオプションの処理マスク.出力配列内の変更される要素を表します
関数 bitwise_and は,各要素のビット毎の論理積を求めます:
2つの配列同士:
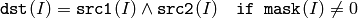
配列とスカラ:
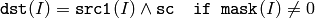
浮動小数点型配列の場合は,マシン固有のビット表現(通常は,IEEE754準拠)が処理に利用されます.また,マルチチャンネル配列の場合,各チャンネルは個別に処理されます.
参考: , ,
cv::bitwise_not¶
- void bitwise_not(const MatND& src, MatND& dst)
配列の各ビットを反転します.
パラメタ: - src1 – 入力配列
- dst – src と同じサイズ,同じ型になるように再割り当てされる出力配列. Mat::create を参照してください
- mask – 8ビットのシングルチャンネル配列であるオプションの処理マスク.出力配列内の変更される要素を表します
関数 bitwise_not は,入力配列の各要素の各ビットを反転します:
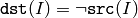
浮動小数点型配列の場合は,マシン固有のビット表現(通常は,IEEE754準拠)が処理に利用されます.また,マルチチャンネル配列の場合,各チャンネルは個別に処理されます.
参考: , ,
cv::bitwise_or¶
- void bitwise_or(const MatND& src1, const MatND& src2, MatND& dst, const MatND& mask=MatND())
- void bitwise_or(const MatND& src1, const Scalar& sc, MatND& dst, const MatND& mask=MatND())
2つの配列同士,あるいは配列とスカラの ビット毎の論理和を求めます.
パラメタ: - src1 – 1番目の入力配列
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- sc – 2番目の入力パラメータであるスカラ
- dst – src と同じサイズ,同じ型になるように再割り当てされる出力配列. Mat::create を参照してください
- mask – 8ビットのシングルチャンネル配列であるオプションの処理マスク.出力配列内の変更される要素を表します
関数 bitwise_or は,各要素のビット毎の論理和を求めます:
2つの配列同士:
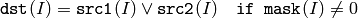
配列とスカラ:
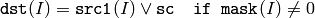
浮動小数点型配列の場合は,マシン固有のビット表現(通常は,IEEE754準拠)が処理に利用されます.また,マルチチャンネル配列の場合,各チャンネルは個別に処理されます.
参考: , ,
cv::bitwise_xor¶
- void bitwise_xor(const MatND& src1, const MatND& src2, MatND& dst, const MatND& mask=MatND())
- void bitwise_xor(const MatND& src1, const Scalar& sc, MatND& dst, const MatND& mask=MatND())
2つの配列同士,あるいは配列とスカラの ビット毎の排他的論理和を求めます.
パラメタ: - src1 – 1番目の入力配列
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- sc – 2番目の入力パラメータであるスカラ
- dst – src1 と同じサイズ,同じ型の出力配列. Mat::create を参照してください
- mask – 8ビットのシングルチャンネル配列であるオプションの処理マスク.出力配列内の変更される要素を表します
関数 bitwise_xor は,各要素のビット毎の排他的論理和を求めます:
2つの配列同士:
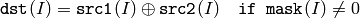
配列とスカラ:
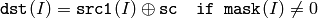
浮動小数点型配列の場合は,マシン固有のビット表現(通常は,IEEE754準拠)が処理に利用されます.また,マルチチャンネル配列の場合,各チャンネルは個別に処理されます.
参考: , ,
cv::calcCovarMatrix¶
- void calcCovarMatrix(const Mat* samples, int nsamples, Mat& covar, Mat& mean, int flags, int ctype=CV_64F)¶
- void calcCovarMatrix(const Mat& samples, Mat& covar, Mat& mean, int flags, int ctype=CV_64F)
ベクトル集合の共分散行列を求めます.
パラメタ: - samples – 個別の行列,あるいは1つの行列の列や行として格納されているサンプル
- nsamples – サンプルが個別の行列に格納されている場合のサンプル数
- covar – 出力される共分散行列. type= ctype の正方行列となります
- mean – 入力,あるいは出力(フラグに依存します)配列 - 入力配列の中間(平均)ベクトル
- flags –
処理フラグ,以下の値の組み合わせです
- CV_COVAR_SCRAMBLED 出力される共分散行列が,以下のように計算されます:
![\texttt{scale} \cdot [ \texttt{vects} [0]- \texttt{mean} , \texttt{vects} [1]- \texttt{mean} ,...]^T \cdot [ \texttt{vects} [0]- \texttt{mean} , \texttt{vects} [1]- \texttt{mean} ,...]](_images/math/131c7329c69299d33cd4cc9c62373a5885db9c5b.png)
, つまり,共分散行列は
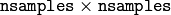 となります.
このような一般的ではない共分散行列は,非常に大きなベクトルの集合に対して高速に PCA(主成分分析)を行うために利用されます(例えば,顔認識のための固有顔の計算など).
この「スクランブルされた」共分散行列の固有値は,真の共分散行列の固有値と一致します.また「真の」固有ベクトルは,「スクランブルされた」共分散行列の固有ベクトルから容易に求めることが出来ます
となります.
このような一般的ではない共分散行列は,非常に大きなベクトルの集合に対して高速に PCA(主成分分析)を行うために利用されます(例えば,顔認識のための固有顔の計算など).
この「スクランブルされた」共分散行列の固有値は,真の共分散行列の固有値と一致します.また「真の」固有ベクトルは,「スクランブルされた」共分散行列の固有ベクトルから容易に求めることが出来ます - CV_COVAR_NORMAL 出力される共分散行列が,以下のように計算されます:
![\texttt{scale} \cdot [ \texttt{vects} [0]- \texttt{mean} , \texttt{vects} [1]- \texttt{mean} ,...] \cdot [ \texttt{vects} [0]- \texttt{mean} , \texttt{vects} [1]- \texttt{mean} ,...]^T](_images/math/8ea3c304dbd969d5def0866d587b87c5d96c6f58.png)
, つまり, covar は各入力ベクトルの要素数と同じサイズの正方行列となります. CV_COVAR_SCRAMBLED と CV_COVAR_NORMAL は,必ずどちらか一方が指定されなければいけません
- CV_COVAR_USE_AVG このフラグが指定されると,関数は入力ベクトルから mean を計算せず,その代わりに,引数で与えられた mean ベクトルを利用します.これは mean があらかじめ計算されている,あるいは分かっている場合,また,共分散行列が部分的に計算されている場合(この場合, mean は入力ベクトルの一部の平均ではなく,全体の平均です)に有用です
- CV_COVAR_SCALE このフラグが指定されると,共分散行列はスケーリングされます.「ノーマル」モードでは, scale は 1./nsamples ,「スクランブル」モードでは, scale は 各ベクトルの要素数の逆数となります.デフォルト(このフラグが指定されない状態)では,共分散行列はスケーリングされません(つまり, scale=1 )
- CV_COVAR_ROWS [2番目の形式においてのみ有効] このフラグは,すべての入力ベクトルが samples 行列の行に格納されていることを意味します.この場合 mean は1行のベクトルです
- CV_COVAR_COLS [2番目の形式においてのみ有効] このフラグは,すべての入力ベクトルが samples 行列の列に格納されていることを意味します.この場合 mean は1列のベクトルです
- CV_COVAR_SCRAMBLED 出力される共分散行列が,以下のように計算されます:
関数 calcCovarMatrix は,共分散行列を求め,またオプションとして入力ベクトル集合の平均ベクトルを計算します.
参考: PCA() , mulTransposed() , Mahalanobis()
cv::cartToPolar¶
- void cartToPolar(const Mat& x, const Mat& y, Mat& magnitude, Mat& angle, bool angleInDegrees=false)¶
2次元ベクトルの角度と大きさを求めます.
パラメタ: - x – x座標の配列.必ず,単精度または倍精度の浮動小数点型配列
- y – x と同じサイズ,同じ型の y 座標の配列
- magnitude – 大きさの出力配列. x と同じサイズ,同じ型
- angle – 角度の出力配列. x と同じサイズ,同じ型.角度はラジアン (
 から
から 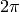 ) あるいは度 (0 から 360) で表されます
) あるいは度 (0 から 360) で表されます - angleInDegrees – 角度の表記にラジアン(デフォルト),または度のどちらを用いるかを指定するフラグ
関数 cartToPolar は,2次元ベクトル集合 (x(I),y(I)) それぞれの大きさと角度のどちらか片方,あるいは両方を求めます:
![\begin{array}{l} \texttt{magnitude} (I)= \sqrt{\texttt{x}(I)^2+\texttt{y}(I)^2} , \\ \texttt{angle} (I)= \texttt{atan2} ( \texttt{y} (I), \texttt{x} (I))[ \cdot180 / \pi ] \end{array}](_images/math/bbfdf84dba415be8bfa0d6db434f1fd388cdcadb.png)
角度は,
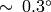 の精度で求められます. (0,0) の場合,その角度は 0 になります.
の精度で求められます. (0,0) の場合,その角度は 0 になります.
cv::checkRange¶
- bool checkRange(const Mat& src, bool quiet=true, Point* pos=0, double minVal=-DBL_MAX, double maxVal=DBL_MAX)¶
- bool checkRange(const MatND& src, bool quiet=true, int* pos=0, double minVal=-DBL_MAX, double maxVal=DBL_MAX)
入力配列の各要素が有効な値であるかどうかをチェックします.
パラメタ: - src – チェックされる配列
- quiet – このフラグが指定されていると,配列の要素が範囲外だった場合には単に false を返します.指定されていなければ,例外を投げます
- pos – 最初のアウトライアの位置が保存される,オプションの出力パラメータ.2番目の形式では, pos がNULLでなければ,必ず src.dims 要素の配列へのポインタとなります
- minVal – 有効範囲の下界(範囲に含みます)
- maxVal – 有効範囲の上界(範囲に含みません)
関数
checkRange
は,配列の各要素が NaN あるいは
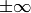 ではないことをチェックします.
minVal < -DBL_MAX
かつ
maxVal < DBL_MAX
である場合,この関数は各値が
minVal
から
maxVal
の範囲に収まっているかどうかもチェックします.マルチチャンネル配列の場合は,各チャンネルは個別に処理されます.もし範囲外の値があれば,その最初の外れ値の位置が
pos
に保存され(
ではないことをチェックします.
minVal < -DBL_MAX
かつ
maxVal < DBL_MAX
である場合,この関数は各値が
minVal
から
maxVal
の範囲に収まっているかどうかもチェックします.マルチチャンネル配列の場合は,各チャンネルは個別に処理されます.もし範囲外の値があれば,その最初の外れ値の位置が
pos
に保存され(
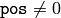 の場合),関数は false を返す(
quiet=true
の場合)か,例外を投げます.
の場合),関数は false を返す(
quiet=true
の場合)か,例外を投げます.
cv::compare¶
- void compare(const MatND& src1, const MatND& src2, MatND& dst, int cmpop)
- void compare(const MatND& src1, double value, MatND& dst, int cmpop)
2つの配列同士,あるいは配列とスカラの各要素を比較します.
パラメタ: - src1 – 1番目の入力配列
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- value – 各配列要素と比較されるスカラ値
- dst – src1 と同じサイズで type= CV_8UC1 である出力配列
- cmpop –
要素同士のチェックすべき関係を指定するフラグ
- CMP_EQ
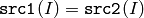 または
または 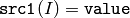
- CMP_GT
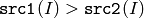 または
または 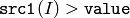
- CMP_GE
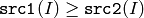 または
または 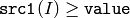
- CMP_LT
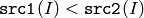 または
または 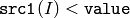
- CMP_LE
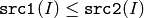 または
または 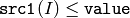
- CMP_NE
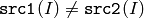 または
または 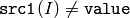
- CMP_EQ
関数 compare は, src1 の各要素と,それに対応する src2 の要素,あるいは実数のスカラ値 value とを比較します. 比較結果が真ならば,出力配列の対応する要素が 255 にセットされ,そうでなければ 0 にセットされます:
- dst(I) = src1(I) cmpop src2(I) ? 255 : 0
- dst(I) = src1(I) cmpop value ? 255 : 0
この比較と等価な処理を,行列表現を用いて表すことも出来ます:
Mat dst1 = src1 >= src2;
Mat dst2 = src1 < 8;
...
参考: checkRange() , min() , max() , threshold() , Matrix Expressions
cv::completeSymm¶
- void completeSymm(Mat& mtx, bool lowerToUpper=false)¶
正方行列の上半分または下半分を,もう半分の側にコピーします.
パラメタ: - mtx – 浮動小数点型の入出力正方行列
- lowerToUpper – true の場合は下半分が上半分にコピーされ,そうでない場合は上半分が下半分にコピーされます
関数 completeSymm は,正方行列の下半分または上半分を逆側の半分にコピーします.このとき,行列の対角成分は,変更されずにそのまま残ります.
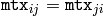 for
for
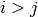 if
lowerToUpper=false
if
lowerToUpper=false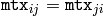 for
for
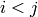 if
lowerToUpper=true
if
lowerToUpper=true
参考: flip() , transpose()
cv::convertScaleAbs¶
- void convertScaleAbs(const Mat& src, Mat& dst, double alpha=1, double beta=0)¶
スケーリング後,絶対値を計算し,結果を結果を 8 ビットに変換します.
パラメタ: - src – 入力配列
- dst – 出力配列
- alpha – オプションのスケールファクタ
- beta – スケーリングされた値に加えられるオプション値
関数 convertScaleAbs は,入力配列の各要素に対して連続した三つの処理を施します:スケーリング,絶対値の計算,符号なし8ビット型への変換:
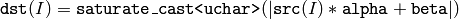
マルチチャンネル配列の場合,関数は各チャンネルを個別に処理します.出力が8ビットでない場合は, Mat::convertTo メソッドを呼び出して(あるいは行列を用いて処理し),さらに結果の絶対値を求めることで同等の処理が可能です.例えば:
Mat_<float> A(30,30);
randu(A, Scalar(-100), Scalar(100));
Mat_<float> B = A*5 + 3;
B = abs(B);
// Mat_<float> B = abs(A*5+3) でも同じことができますが
// その場合,テンポラリ行列が確保されます.
参考: Mat::convertTo() , abs()
cv::countNonZero¶
- int countNonZero(const MatND& mtx)
0 ではない配列要素を数えます.
Parameter: mtx – シングルチャンネルの配列
関数 cvCountNonZero は,mtx 内の 0 ではない要素の数を返します:
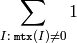
参考: mean() , meanStdDev() , norm() , minMaxLoc() , calcCovarMatrix()
cv::cubeRoot¶
- float cubeRoot(float val)¶
引数の3乗根を求めます.
Parameter: val – この関数の引数
関数
cubeRoot
は,
![\sqrt[3]{\texttt{val}}](_images/math/82540f5fd7cb0fee8d4e8fc93aeea6bb2b23054a.png) を求めます.負の値も正しく扱うことができますが,
NaN
や
を求めます.負の値も正しく扱うことができますが,
NaN
や
 は扱えません.精度は,単精度データに対して可能な最大精度とほぼ等しくなります.
は扱えません.精度は,単精度データに対して可能な最大精度とほぼ等しくなります.
cv::cvarrToMat¶
- Mat cvarrToMat(const CvArr* src, bool copyData=false, bool allowND=true, int coiMode=0)¶
CvMat, IplImage または CvMatND を cv::Mat に変換します.
パラメタ: - src – 変換元の CvMat , IplImage または CvMatND
- copyData – これが偽の場合(デフォルト)は,データはコピーされずに新しいヘッダのみが作成されます.この場合,新しいヘッダが利用されている間は元の配列が解放されないようにしなければいけません.このパラメータが真の場合は,すべてのデータがコピーされるので,ユーザは変換後に元の配列を解放しても構いません
- allowND – これが真の場合(デフォルト), CvMatND は,可能ならば(例えば,データが連続) Mat に変換されます.それが不可能,あるいはパラメータが偽の場合,この関数はエラーを返します
- coiMode –
IplImage COI が設定されている場合に,その扱い方を指定するパラメータ.
- coiMode=0 の場合,COI が設定されていれば関数はエラーを返します.
- coiMode=1 の場合,関数はエラーを返しません.その代わり,元画像全体のヘッダを返すので,ユーザはそれをチェックし COI を手動で処理する必要があります. extractImageCOI() を参照してください.
関数 cvsrcToMat は, CvMat , IplImage または CvMatND のヘッダを Mat() のヘッダに変換します.その際に,オプションとして内部データを複製することもできます.作成されたヘッダは,この関数の戻り値となります.
copyData=false の場合,変換は非常に高速に(O(1)の定数時間で)行われ,新たに作成された行列ヘッダは refcount=0 となります. これは,行列データに対して参照カウントが行われないことを意味するので,ユーザは新しいヘッダが解放されるまでの間データを保持しておく必要があります.つまり,
cvsrcToMat(src, true)
 cvsrcToMat(src, false).clone()
(COIはセットされていないものとします).この関数は,新しい形式のデータ構造を内部的に利用するためにデータを移行するコード内部で,
CvArr
の枠組みをサポートする一貫した方法を提供します.また,
Mat()
から
CvMat
や
IplImage
への逆変換は,単純な代入によって行うことができます:
cvsrcToMat(src, false).clone()
(COIはセットされていないものとします).この関数は,新しい形式のデータ構造を内部的に利用するためにデータを移行するコード内部で,
CvArr
の枠組みをサポートする一貫した方法を提供します.また,
Mat()
から
CvMat
や
IplImage
への逆変換は,単純な代入によって行うことができます:
CvMat* A = cvCreateMat(10, 10, CV_32F);
cvSetIdentity(A);
IplImage A1; cvGetImage(A, &A1);
Mat B = cvarrToMat(A);
Mat B1 = cvarrToMat(&A1);
IplImage C = B;
CvMat C1 = B1;
// A, A1, B, B1, C, C1 は
// 同じ 10x10 の浮動小数点型配列に対する別々のヘッダ.
// C, C1 を OpenCV の関数に渡す場合には
// "&" が必要なことに注意してください.例えば:
printf("
この関数は通常,古い形式の2次元配列( CvMat や IplImage )を Mat に変換するために利用されますが,入力として CvMatND を受け取り,可能ならばそこから Mat() を作成することもできます.ある CvMatND A において,すべて(そ れが1次元でも可)の次元 i, 0 < i < A.dims に対して A.dim[i].size*A.dim.step[i] == A.dim.step[i-1] の場合に限り変換が可能です.つまり,行列データは連続であるか,連続した行列のシーケンスとして表現可能なものでなくてはいけません.この関数をこの様に使うことで, CvMatND に任意の要素単位の処理関数を適用できます.しかし,フィルタリング関数のような,より複雑な処理ではうまく動作しないので,コンストラクタを利用して CvMatND を MatND() に変換する必要があります.
最後のパラメータ coiMode は,COI が設定された画像の扱い方を指定します:デフォルト値である 0 の場合,COI が設定された画像が入力されると関数はエラーを発生させます. coiMode=1 は,エラーが起こらないことを意味するので,ユーザは COI が設定されているかどうかをチェックして,それを手動で処理しなければいけません. Mat() や MatND() などの新しい構造体は,COI をネイティブにはサポートしていません.新しい形式の配列の個々のチャンネルを処理するためには,(例えば,行列のイテレータを利用して)配列を横断するループを作り COI を処理するか,あるいは mixChannels() (新しい形式用)や extractImageCOI() (古い形式用)を用いて COI を抽出し,その個々のチャンネルを処理した後,必要ならば( mixChannel() や insertImageCOI() を用いて)出力配列の中に戻す,といった手段が必要になります.
参考: cvGetImage() , cvGetMat() , cvGetMatND() , extractImageCOI() , insertImageCOI() , mixChannels()
cv::dct¶
- void dct(const Mat& src, Mat& dst, int flags=0)¶
1次元あるいは2次元の配列に対して,離散コサイン変換または逆変換を行います.
パラメタ: - src – 浮動小数点型の入力配列
- dst – src と同じサイズ,同じ型の出力配列
- flags –
変換フラグ,以下の値の組み合わせ
- DCT_INVERSE デフォルトの順変換の代わりに,1次元あるいは2次元の逆変換を行います
- DCT_ROWS 入力行列の各行に対して,順変換あるいは逆変換を行います.このフラグによって,ユーザは複数のベクトルを同時に変換することができます.また,(処理時間の何倍もかかることがある)オーバーヘッドを減らしたり,3次元以上の変換を行うために利用することもできます
関数 dct は,1次元または2次元の浮動小数点型配列に対して離散コサイン変換(DCT)または逆変換を行います:
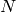 要素の1次元ベクトルのコサイン変換:
要素の1次元ベクトルのコサイン変換:
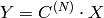
ここで
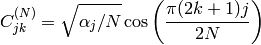
また
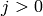 に対して
に対して
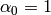 ,
,
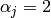 です.
です.
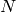 要素の1次元ベクトルの逆コサイン変換:
要素の1次元ベクトルの逆コサイン変換:
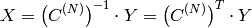
(
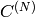 は対角行列なので,
は対角行列なので,
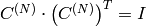 となります)
となります)
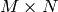 の行列のコサイン変換:
の行列のコサイン変換:
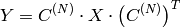
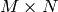 の行列の逆コサイン変換:
の行列の逆コサイン変換:
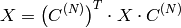
この関数は,フラグと入力配列のサイズを見て処理モードを選択します:
- (flags & DCT_INVERSE) == 0 の場合,1次元または2次元の順変換を行います.そうでない場合は,1次元または2次元の逆変換を行います.
- (flags & DCT_ROWS)
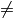 0
の場合,各行に対して1次元の変換を行います.
0
の場合,各行に対して1次元の変換を行います. - そうでない場合で,かつ配列が1列あるいは1行ならば,1次元の変換を行います.
- そうでなければ,2次元の変換を行います.
重要な注意 :現在の cv::dct は,偶数サイズの配列(2, 4, 6 ...)をサポートしています.データ分析や近似の際には,必要ならば配列にダミーの値を詰めてサイズを調整できます.
また,この関数の性能は配列のサイズに非常に依存します(が,単調依存ではありません).これに関しては
getOptimalDFTSize()
を参照してください.現在の実装では,サイズ
N
のベクトルの DCT は,
N/2
サイズの DFT を介して計算されます.よって,最適な DCT サイズ
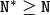 は以下のように求めることができます:
は以下のように求めることができます:
size_t getOptimalDCTSize(size_t N) { return 2*getOptimalDFTSize((N+1)/2); }
参考: dft() , getOptimalDFTSize() , idct()
cv::dft¶
- void dft(const Mat& src, Mat& dst, int flags=0, int nonzeroRows=0)¶
1次元あるいは2次元の配列に対して,離散フーリエ変換または逆変換を行います.
パラメタ: - src – 実数または複素数の入力配列
- dst – flags に依存してサイズと型が決まる出力配列
- flags –
変換フラグ,以下の値の組み合わせ
- DFT_INVERSE デフォルトの順変換の代わりに,1次元あるいは2次元の逆変換を行います
- DFT_SCALE 結果を配列の要素数で割ってスケーリングを行います.通常,これは DFT_INVERSE と一緒に利用されます
- DFT_ROWS 入力行列の各行に対して,順変換あるいは逆変換を行います.このフラグによって,ユーザは複数のベクトルを同時に変換することができます.また,(処理時間の何倍もかかることがある)オーバーヘッドを減らしたり,3次元以上の変換を行うために利用することもできます
- DFT_COMPLEX_OUTPUT 実数の1次元配列または2次元配列の順変換を行う場合,その結果は複素配列となりますが,これは複素共役対称( CCS )です.以下の説明を参照してください.入力配列と同サイズの実数配列にパックされた配列を作ることは,最速の選択であり,関数のデフォルトの動作でもあります.しかし,(簡易スペクトル分析などの為に)正確な複素配列を得たい場合もあるかもしれません.このフラグを渡すことで,正確なサイズの複素配列を出力するようにできます
- DFT_REAL_OUTPUT 実数の1次元配列または2次元配列の逆変換を行う場合,その結果は通常,同じサイズの複素配列となります.しかし,入力配列が複素共役対称である場合(例えば, DFT_COMPLEX_OUTPUT フラグを指定した順変換の結果)は,出力は実数配列になります.この関数自身は入力が対称かそうでないかをチェックしませんが,このフラグを渡すことで,対称性を仮定して実数配列を作成します.入力配列がパックされた実数配列で,その逆変換が実行される場合,この関数は入力をパックされた複素共役対称配列として扱うので,出力も実数配列となることに注意してください
- nonzeroRows – このパラメータが
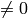 の場合,関数は入力配列の最初の nonzeroRows 行だけ( DFT_INVERSE がセットされていない),あるいは,出力配列の最初の nonzeroRows 行だけ( DFT_INVERSE がセットされている )が 0 ではない値を含むと仮定し,残りの行をより効率的に処理することで計算時間を短縮します.このテクニックは,DFT を用いた配列の相互相関や畳み込みの計算で非常に役立ちます
の場合,関数は入力配列の最初の nonzeroRows 行だけ( DFT_INVERSE がセットされていない),あるいは,出力配列の最初の nonzeroRows 行だけ( DFT_INVERSE がセットされている )が 0 ではない値を含むと仮定し,残りの行をより効率的に処理することで計算時間を短縮します.このテクニックは,DFT を用いた配列の相互相関や畳み込みの計算で非常に役立ちます
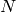 要素の1次元ベクトルのフーリエ変換:
要素の1次元ベクトルのフーリエ変換:
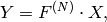
ここで
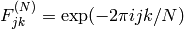 ,
,
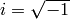
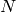 要素の1次元ベクトルの逆フーリエ変換:
要素の1次元ベクトルの逆フーリエ変換:
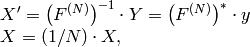
ここで
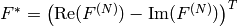
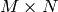 の2次元ベクトルのフーリエ変換:
の2次元ベクトルのフーリエ変換:
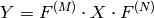
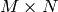 の2次元ベクトルの逆フーリエ変換:
の2次元ベクトルの逆フーリエ変換:
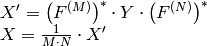
実数(シングルチャンネル)データの場合,フーリエ変換の結果や逆フーリエ変換の入力を表すために,IPL で利用されていた CCS (複素共役対称)と呼ばれるパックされた形式が利用されます:
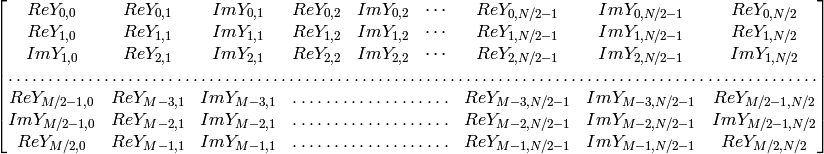
1次元の実数ベクトルの変換の場合,出力は上述の行列の1行目のようになります.
また,この関数は,フラグと入力配列のサイズに依存する処理モードを選択します:
- DFT_ROWS がセットされているか,入力配列が1行/1列である場合,この関数は1次元の順変換または逆変換を( DFT_ROWS がセットされている場合は,行列の各行に対して)行います.そうでない場合は,2次元の変換を行います.
- 入力配列が実数,かつ
DFT_INVERSE
がセットされていない場合,この関数は1次元または2次元の順変換を行います:
- DFT_COMPLEX_OUTPUT がセットされている場合,入力と同じサイズの複素行列が出力されます.
- そうでない場合,入力と同じサイズの実数行列が出力されます.2次元変換の場合,前述のパックされた形式が利用されます.また1次元変換の場合は,前述の行列の1行目のようになります.( DCT_ROWS を利用した)複数の1次元変換の場合,出力行列の各行が前述の行列の1行目のようになります.
- そうでない場合,入力配列が複素数で DFT_INVERSE と DFT_REAL_OUTPUT がセットされていない場合,入力と同じサイズの複素配列が出力されます.この関数は,フラグ DFT_INVERSE に依存して,1次元か2次元の,順変換または逆変換を選択します.また,フラグ DFT_ROWS に依存して,入力配列全体あるいは各行に対して変換を行います.
- それ以外,つまり DFT_INVERSE がセットされており,入力配列が実数の場合,あるいは複素数ではあるが DFT_REAL_OUTPUT がセットされている場合,入力と同じサイズの実数行列が出力されます.この関数は,フラグ DFT_INVERSE に依存して,1次元か2次元順変換または逆変換を選択します.また,フラグ DFT_ROWS に依存して,入力配列全体あるいは各行に対して変換を行います.
もし DFT_SCALE がセットされていれば,変換後にスケーリングが行われます.
dct() とは異なり,この関数は任意サイズの配列をサポートしますが,効率的に処理できるのは,小さい素数(現在の実装では 2, 3, 5)の積で量子化されたサイズの配列のみです.このような効率的な DFT サイズは, getOptimalDFTSize() メソッドを用いて求めることができます.
ここでは,DFT を利用した実数の2次元配列の畳み込み計算の方法を示します:
void convolveDFT(const Mat& A, const Mat& B, Mat& C)
{
// 必要なら出力配列の再割り当てを行います.
C.create(abs(A.rows - B.rows)+1, abs(A.cols - B.cols)+1, A.type());
Size dftSize;
// DFT変換のサイズを計算します.
dftSize.width = getOptimalDFTSize(A.cols + B.cols - 1);
dftSize.height = getOptimalDFTSize(A.rows + B.rows - 1);
// テンポラリバッファを確保し,0で初期化します
Mat tempA(dftSize, A.type(), Scalar::all(0));
Mat tempB(dftSize, B.type(), Scalar::all(0));
// A と B をそれぞれ tmpA と tmpB の左上の角にコピーします.
Mat roiA(tempA, Rect(0,0,A.cols,A.rows));
A.copyTo(roiA);
Mat roiB(tempB, Rect(0,0,B.cols,B.rows));
B.copyTo(roiB);
// パックされた A と B を変換し置換します.
// 処理を高速化するために "nonzeroRows" を利用します.
dft(tempA, tempA, 0, A.rows);
dft(tempB, tempB, 0, B.rows);
// スペクトルの積を求めます;
// この関数は,スペクトルのパックされた表現を扱うことができます.
mulSpectrums(tempA, tempB, tempA);
// 結果を周波数領域から逆変換します.
// すべての行が 0 でないとしても
// 必要なのは C.rows だけなので
// nonzeroRows == C.rows を渡します.
dft(tempA, tempA, DFT_INVERSE + DFT_SCALE, C.rows);
// 結果をコピーして C に戻します.
tempA(Rect(0, 0, C.cols, C.rows)).copyTo(C);
// すべてのテンポラリバッファは自動的に解放されます.
}
上述のサンプルで,最適化できる箇所はどこでしょうか?
- 順変換の際に
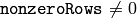 を渡し,
A
/
B
をそれぞれ
tempA
/
tempB
の左上角にコピーするので,
tempA
と
tempB
の全体をクリアする必要はありません.クリアの必要があるのは,右端の
tempA.cols - A.cols
(
tempB.cols - B.cols
) 列だけです.
を渡し,
A
/
B
をそれぞれ
tempA
/
tempB
の左上角にコピーするので,
tempA
と
tempB
の全体をクリアする必要はありません.クリアの必要があるのは,右端の
tempA.cols - A.cols
(
tempB.cols - B.cols
) 列だけです. - 特に B が A と比べて非常に小さい場合,あるいはその逆の場合,DFT に基づく畳み込みを巨大な配列全体に適用する必要はありません.その代わりに,部分的な畳み込みを行います.部分的な評価のために,出力配列 C を複数のタイルに分割する必要があります.そして A と B にあたる部分は,このタイルでの畳み込みを計算する必要があります. C のタイルが小さすぎる場合,繰り返し作業の為に計算速度が大きく低下します.極端な話, C の各タイルが1つのピクセルだとすると,このアルゴリズムは元の畳み込みアルゴリズムと同じになってしまいます.また,タイルが大きすぎる場合,テンポラリ配列 tempA と tempB が巨大になり,キャッシュの局所性が減少することで,やはり計算速度が低下します.つまり,これらの中間のどこかに,最適なタイルサイズが存在します.
- 部分的な畳み込み計算が可能ならば, C の異なるタイルを並列に計算できるため,ループをスレッド化することが可能です.
上記の改良はすべて, matchTemplate() と filter2D() に実装されているので,これらの関数を用いると,上述の理論的に最適な実装を利用するよりも良い性能を得られます(これら2つの関数は実際には畳み込みではなく相互相関を計算するので, flip() を利用してカーネルか画像をその中心で「反転」させる必要があります).
参考: dct() , getOptimalDFTSize() , mulSpectrums() , filter2D() , matchTemplate() , flip() , cartToPolar() , magnitude() , phase()
cv::divide¶
- void divide(const MatND& src1, const MatND& src2, MatND& dst, double scale=1)
- void divide(double scale, const MatND& src2, MatND& dst)
2つの配列同士,あるいは配列とスカラの 要素毎の商を求めます.
パラメタ: - src1 – 1番目の入力配列
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- scale – スケールファクタ
- dst – src2 と同じサイズ,同じ型である出力配列
関数 divide は,ある配列を別の配列で割ります:
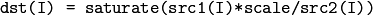
あるいは,スカラを配列で割ります.この場合 src1 は存在しません:
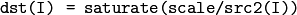
結果は, src1 と同じ型になります. src2(I)=0 の場合は,結果も dst(I)=0 となります.
参考: multiply() , add() , subtract() , Matrix Expressions
cv::determinant¶
- double determinant(const Mat& mtx)¶
浮動小数点型の正方行列の行列式を返します.
Parameter: mtx – 入力行列; CV_32FC1 か CV_64FC1 型で正方でなければいけません
関数 determinant は,指定された行列の行列式を求め,それを返します. 小さい行列( mtx.cols=mtx.rows<=3 )に対しては直接法を利用し,大きい行列に対しては LU 分解を利用します.
正値対称行列に対しては,
SVD()
を計算することも可能です:
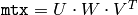 .そして,
.そして,
 の対角成分の積として行列式を求めます.
の対角成分の積として行列式を求めます.
参考: SVD() , trace() , invert() , solve() , Matrix Expressions
cv::eigen¶
- bool eigen(const Mat& src, Mat& eigenvalues, Mat& eigenvectors, int lowindex=-1, int highindex=-1)
対称行列の固有値及び固有ベクトルを求めます.
パラメタ: - src – 入力行列. CV_32FC1 または CV_64FC1 型で,正方な対称行列でなければいけません:
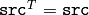
- eigenvalues – src と同じ型の固有値.固有値は,降順に格納されます
- eigenvectors – 固有ベクトルの行列. src と同じサイズ,同じ型.固有ベクトルは,対応する固有値と同じ順番で行列の行として保存されます
- lowindex – オプション.求める最大の固有値/固有ベクトルのインデックス(下記参照)
- highindex – オプション.求める最小の固有値/固有ベクトルのインデックス(下記参照)
- src – 入力行列. CV_32FC1 または CV_64FC1 型で,正方な対称行列でなければいけません:
関数 eigen は,対称行列 src の固有値のみ,または固有値と固有ベクトルの両方を求めます:
src*eigenvectors(i,:)' = eigenvalues(i)*eigenvectors(i,:)' (in MATLAB notation)
lowindex あるいは highindex の一方が与えられると,もう片方も必要になります.インデックス番号は 0 から始まります.例えば,最大の固有値/固有ベクトルを計算する場合は, lowindex = highindex = 0 をセットします.過去の経緯から,この関数は常に入力行列と同じサイズの正方行列(固有ベクトルから構成)と,入力行列と同じ長さのベクトル(固有値から構成)を返します.インデックスで選択された固有値/固有ベクトルは,常に最初の highindex - lowindex + 1 行目保存されます.
参考: SVD() , completeSymm() , PCA()
cv::exp¶
- void exp(const MatND& src, MatND& dst)
各配列要素を指数として,自然対数の底(ネイピア数)e のべき乗を求めます.
パラメタ: - src – 入力配列
- dst – src と同じサイズ,同じ型の出力配列
関数 exp は,入力配列の各要素に対して,それを指数とする自然対数の底eのべき乗を求めます:
![\texttt{dst} [I] = e^{ \texttt{src} }(I)](_images/math/13e517b3da9ab628878368589320811cfd644cd0.png)
最大誤差は,単精度で約
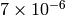 ,倍精度で
,倍精度で
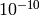 未満です.現在の実装では,指数表現されない(非正規化)浮動小数点数は出力時に 0 に変換されます.また,特殊な値(NaN,
未満です.現在の実装では,指数表現されない(非正規化)浮動小数点数は出力時に 0 に変換されます.また,特殊な値(NaN,
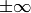 )は扱いません.
)は扱いません.
参考: log() , cartToPolar() , polarToCart() , phase() , pow() , sqrt() , magnitude()
cv::extractImageCOI¶
- void extractImageCOI(const CvArr* src, Mat& dst, int coi=-1)¶
画像の選択されたチャンネルを抽出します.
パラメタ: - src – 入力配列. CvMat または IplImage へのポインタ
- dst – シングルチャンネルで, src と同じサイズ,同じビット深度の出力配列
- coi – このパラメータが >=0 の場合は,それは抽出するチャンネルを表します. <0 の場合は, src が有効な COI を持つ IplImage へのポインタでなけらばならず,そこで選択された COI が抽出されます
関数 extractImageCOI は,古い形式の配列から画像の COI を抽出し,それを新しい形式の C++ 行列に配置するために利用されます.他の関数と同様に,必要ならば Mat::create によって出力行列が再割り当てされます.
新しい形式の行列からチャンネルを抽出するには mixChannels() や split() を利用してください.
参考: mixChannels() , split() , merge() , cvarrToMat() , cvSetImageCOI() , cvGetImageCOI()
cv::fastAtan2¶
- float fastAtan2(float y, float x)¶
2次元ベクトルの角度(度単位)を求めます.
パラメタ: - x – ベクトルの x 座標
- y – ベクトルの y 座標
関数
fastAtan2
は,2次元の入力ベクトルの角度を求めます.角度は度単位で表現され,
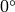 から
から
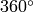 の範囲で変化します.精度は約
の範囲で変化します.精度は約
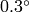 です.
です.
cv::flip¶
- void flip(const Mat& src, Mat& dst, int flipCode)¶
2次元配列を,垂直軸,水平軸,あるいはその両方の軸で反転します.
パラメタ: - src – 入力配列
- dst – src と同じサイズ,同じ型の出力配列
- flipCode –
配列の反転方法の指定:
0 は x軸周りでの反転,正値(例えば,1)は y軸周りでの反転,負値(例えば,-1)は 両軸周りでの反転を表します.以下の式と説明も参照してください
関数 flip は,3種類の中から1つ選択された方法で配列を反転させます(行と列のインデックスは0が基準):
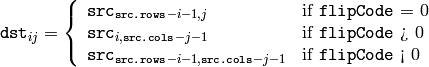
この関数を利用するケースとして,以下のような場合が考えられます:
- 左上原点画像と左下原点画像の変換をするための画像の上下反転(
 ).これは,Windows のビデオ画像処理でよく利用されます.
).これは,Windows のビデオ画像処理でよく利用されます. - 垂直軸に対する線対称性を調べるための左右反転(
 ),反転後に水平シフトして差の絶対値を計算します.
),反転後に水平シフトして差の絶対値を計算します. - 中心点に対する点対称性を調べるための上下,左右の同時反転(
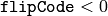 ),反転後にシフトして差の絶対値を計算します.
),反転後にシフトして差の絶対値を計算します. - 1次元配列の順番を逆転(
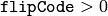 または
または
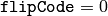 )
)
参考: transpose() , repeat() , completeSymm()
cv::gemm¶
- void gemm(const Mat& src1, const Mat& src2, double alpha, const Mat& src3, double beta, Mat& dst, int flags=0)¶
汎用的な行列の乗算を行います.
パラメタ: - src1 – 操作される1番目の入力行列.型は CV_32FC1 , CV_64FC1 , CV_32FC2 または CV_64FC2 のいずれか
- src2 – 操作される2番目の入力行列. src1 と同じ型
- alpha – 行列積の重み
- src3 – オプション.行列積に加算される3番目の行列. src1 や src2 と同じ型
- beta – src3 の重み
- dst – 出力行列.適切なサイズを持ち,入力行列と同じ型
- flags –
処理フラグ:
- GEMM_1_T src1 を転置
- GEMM_2_T src2 を転置
- GEMM_3_T src3 を転置
この関数は,汎用的な行列の乗算を行うもので,対応する BLAS レベル 3 の *gemm 関数に似ています. 例えば, gemm(src1, src2, alpha, src3, beta, dst, GEMM_1_T + GEMM_3_T) は以下に相当します.
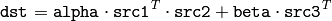
この関数は,行列の式で置き換えることができます.例えば,上述の例は以下のように置き換えが可能です:
dst = alpha*src1.t()*src2 + beta*src3.t();
参考: mulTransposed() , transform() , Matrix Expressions
cv::getConvertElem¶
- ConvertData getConvertElem(int fromType, int toType)¶
- ConvertScaleData getConvertScaleElem(int fromType, int toType)¶
- typedef void (*ConvertData)(const void* from, void* to, int cn)¶
- typedef void (*ConvertScaleData)(const void* from, void* to, int cn, double alpha, double beta)¶
1ピクセルに対する変換関数を返します.
パラメタ: - fromType – 入力ピクセルの型
- toType – 出力ピクセルの型
- from – コールバックパラメータ:入力ピクセルへのポインタ
- to – コールバックパラメータ:出力ピクセルへのポインタ
- cn – コールバックパラメータ:チャンネル数.任意の値,1, 100, 100000, ...
- alpha – オプション.ConvertScaleData コールバックパラメータ:スケールファクタ
- beta – オプション.ConvertScaleData コールバックパラメータ:デルタまたはオフセット
関数 getConvertElem および getConvertScaleElem は,個々のピクセルをある型から別の型に変換する関数へのポインタを返します. この関数の主な目的は1ピクセルの変換ですが(実際は,疎な行列をある型から別の型に変換するため),行列データが連続ならば, cn = matrix.cols*matrix.rows*matrix.channels() を設定することで,密な行列の行全体,あるいは行列全体を一度に変換することができます.
参考: Mat::convertTo() , MatND::convertTo() , SparseMat::convertTo()
cv::getOptimalDFTSize¶
- int getOptimalDFTSize(int vecsize)¶
与えられたベクトルサイズに対して最適な DFT サイズを返します.
Parameter: vecsize – ベクトルサイズ
DFT の性能は,ベクトルサイズの単調関数ではありません.よって,2つの配列の畳み込みや配列のスペクトル分析を行う場合に,入力データに0を埋め込んで,元の配列よりも高速に変換できる少しだけ大きい配列を得るというのは妥当な処理と言えます.
サイズが2の累乗である配列が最も高速に処理できますが,サイズが 2, 3, 5 の積(例えば,300 = 5*5*3*2*2)である配列も非常に効率的に処理可能です.
関数
getOptimalDFTSize
は,
vecsize
以上の値で,サイズ
N
のベクトルの DFT が効率的に計算できるような最小の値
N
を返します.現在の実装では,ある
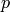 ,
,
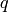 ,
,
 に対して
に対して
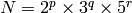 となります.
となります.
vecsize が大きすぎる( INT_MAX に非常に近い)場合,この関数は負の値を返します.
DCT に対する最適なベクトルサイズを推定するのに,この関数を直接利用することはでません(現在の DCT の実装では,偶数サイズのベクトルのみをサポートしているので)が, getOptimalDFTSize((vecsize+1)/2)*2 とすれば簡単に求めることが可能です.
参考: dft() , dct() , idft() , idct() , mulSpectrums()
cv::idct¶
- void idct(const Mat& src, Mat& dst, int flags=0)¶
1次元あるいは2次元の配列に対して,逆離散コサイン変換または逆変換を行います.
パラメタ: - src – シングルチャンネル,浮動小数点型の入力配列
- dst – src と同じサイズ,同じ型の出力配列
- flags – 処理フラグ
idct(src, dst, flags) は, dct(src, dst, flags | DCT_INVERSE) と等価です. 詳しくは dct() を参照してください.
参考: dct() , dft() , idft() , getOptimalDFTSize()
cv::idft¶
- void idft(const Mat& src, Mat& dst, int flags=0, int outputRows=0)¶
1次元あるいは2次元の配列に対して,逆離散フーリエ変換を行います.
パラメタ:
idft(src, dst, flags) は dct(src, dst, flags | DFT_INVERSE) と等価です.詳しくは dft() を参照してください. dft と idft は,デフォルトでは結果をスケーリングしないことに注意してください.したがって,互いに逆変換を行う場合は, dft と idft のどちらか片方に DFT_SCALE を渡さなければいけません.
参考: dft() , dct() , idct() , mulSpectrums() , getOptimalDFTSize()
cv::inRange¶
- void inRange(const MatND& src, const MatND& lowerb, const MatND& upperb, MatND& dst)
- void inRange(const MatND& src, const Scalar& lowerb, const Scalar& upperb, MatND& dst)
ある配列要素が,別の2つの配列要素で表される範囲内に収まっているかをチェックします.
パラメタ: - src – 1番目の入力配列
- lowerb – src と同じサイズ同じ型の,範囲の下界を表す配列(範囲に含みます)
- upperb – src と同じサイズ同じ型の,範囲の上界を表す配列(範囲に含みません)
- dst – src と同じサイズで,型が CV_8U である出力配列
関数 inRange は,入力配列の各要素に対して範囲チェックを行います:
シングルチャンネル配列の場合は,
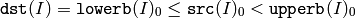
となり,2チャンネル以上の配列の場合も同様になります.
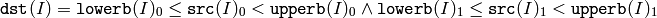
dst (I) は, src (I) が指定した範囲内にある場合は 255(すべてのビットが 1 )にセットされ,そうでない場合は 0 にセットされます.
cv::invert¶
- double invert(const Mat& src, Mat& dst, int method=DECOMP_LU)¶
行列の逆行列,または擬似逆行列を求めます.
パラメタ: - src – 浮動小数点型で
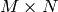 の入力行列
の入力行列 - dst – src と同じ型で
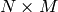 の出力行列
の出力行列 - flags –
逆行列を求める手法:
- DECOMP_LU 最適なピボット選択を行うガウスの消去法
- DECOMP_SVD 特異値分解(SVD)法
- DECOMP_CHOLESKY コレスキー分解.行列は対称かつ正定値でなければならりません
- src – 浮動小数点型で
関数
invert
は,行列
src
の逆行列を求め,結果を
dst
に格納します.
src
が正則でない場合,この関数は擬似逆行列, つまり
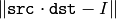 を最小にする
dst
を求めます.
を最小にする
dst
を求めます.
DECOMP_LU メソッドを利用する場合,この関数は src の行列式を返します( src は必ず正方 ).これが 0 の場合,逆行列は求まらずに dst は 0 で埋められます.
DECOMP_SVD メソッドを利用する場合,この関数は src の条件数の逆数(最大の特異値に対する最小の特異値の比)を返しますが, src が特異行列の場合は 0 を返します. src が特異行列の場合,SVD メソッドは擬似逆行列を求めます.
DECOMP_LU と同様に, DECOMP_CHOLESKY メソッドも正則な行列の場合のみ利用できます.逆行列が求まれば,それを dst に格納して 0 ではない値を返し,そうでなければ 0を返します.
cv::log¶
- void log(const MatND& src, MatND& dst)
各配列要素の絶対値の自然対数を求めます.
パラメタ: - src – 入力配列
- dst – src と同じサイズ,同じ型の出力配列
関数 log は,入力配列の各要素の絶対値の自然対数を求めます:
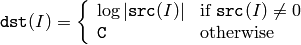
ここで
C
は,大きな負の値を表します(現在の実装では,およそ -700).
最大相対誤差は,単精度の入力に対して約
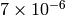 ,倍精度の入力に対して
,倍精度の入力に対して
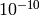 未満です.特殊な値(NaN,
未満です.特殊な値(NaN,
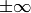 )は扱いません.
)は扱いません.
参考: exp() , cartToPolar() , polarToCart() , phase() , pow() , sqrt() , magnitude()
cv::LUT¶
- void LUT(const Mat& src, const Mat& lut, Mat& dst)¶
ルックアップテーブルを用いて配列を変換します.
パラメタ: - src – 各要素が 8 ビットの入力配列
- lut – 256 要素のルックアップテーブル.入出力配列がマルチチャンネルの場合,ルックアップテーブルは,シングルチャンネル(この場合は,各チャンネルに対して同じテーブルを使う),あるいは入出力配列と同じチャンネル数である必要があります
- dst – src と同じサイズ,同じチャンネル数の出力配列.ビット深度は lut と等しくなります
関数 LUT は,ルックアップテーブルから取り出した値で出力配列を埋めます.テーブルの要素を指定するインデックスには,入力配列の値が用いられます.つまり,この関数は src の各要素を以下のように処理します:
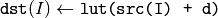
ここで,
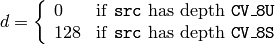
参考: convertScaleAbs() , Mat::convertTo
cv::magnitude¶
- void magnitude(const Mat& x, const Mat& y, Mat& magnitude)¶
2次元ベクトルの大きさを求めます.
パラメタ: - x – ベクトルの x 座標の浮動小数点型配列
- y – ベクトルの y 座標の浮動小数点型配列. x と同じサイズ
- dst – x と同じサイズ,同じ型の出力配列
関数 magnitude は, x と y の配列要素で表された2次元ベクトルの大きさを求めます:
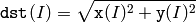
参考: cartToPolar() , polarToCart() , phase() , sqrt()
cv::Mahalanobis¶
- double Mahalanobis(const Mat& vec1, const Mat& vec2, const Mat& icovar)¶
2つのベクトル間のマハラノビス距離を求めます.
パラメタ: - vec1 – 1番目の1次元入力ベクトル
- vec2 – 2番目の1次元入力ベクトル
- icovar – 共分散行列の逆行列
関数 cvMahalonobis は,2つのベクトル間の重み付き距離を求め,それを返します:
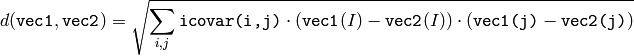
共分散行列を関数 calcCovarMatrix() を用いて計算し,関数 invert() を用いてその逆行列を求ます(精度良く計算するために,なるべく DECOMP _ SVD メソッドを利用してください).
cv::max¶
- Mat_Expr<...> max(const Mat& src1, double value)
- Mat_Expr<...> max(double value, const Mat& src1)
- void max(const MatND& src1, const MatND& src2, MatND& dst)
- void max(const MatND& src1, double value, MatND& dst)
2つの配列同士,あるいは配列とスカラの 要素毎の最大値を求めます.
パラメタ: - src1 – 1番目の入力配列
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- value – 実数のスカラ値
- dst – src1 と同じサイズ,同じ型である出力配列
関数 max は,2つの配列の要素を比較し大きい方を求めます:
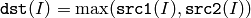
または,配列とスカラの比較:
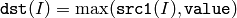
配列とスカラを引数にとる場合,入力配列がマルチチャンネルならば,各チャンネルは個別に value と比較されます.
上述したこの関数のバリエーションのうち,最初の三つの形式は,実際には Matrix Expressions の一部です.これらは行列表現オブジェクトを返します.そして,それをさらに変換したり,行列に代入したり,関数に渡したりできます.
参考: min() , compare() , inRange() , minMaxLoc() , Matrix Expressions
cv::mean¶
- Scalar mean(const MatND& mtx)
- Scalar mean(const MatND& mtx, const MatND& mask)
配列要素の平均値を求めます.
パラメタ: - mtx – 入力配列.(結果を Scalar() に格納出来るように)1から4までのチャンネルを持ちます
- mask – オプションである処理マスク
関数 mean は,各チャンネル毎に配列要素の平均値 M を求め,それを返します:
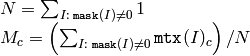
すべてのマスク要素が 0 の場合,この関数は Scalar::all(0) を返します.
参考: countNonZero() , meanStdDev() , norm() , minMaxLoc()
cv::meanStdDev¶
- void meanStdDev(const MatND& mtx, Scalar& mean, Scalar& stddev, const MatND& mask=MatND())
配列要素の平均と標準偏差を求めます.
パラメタ: - mtx – 入力配列.(結果を Scalar() に格納出来るように)1から4までのチャンネルを持ちます
- mean – 出力パラメータ.求められた平均値
- stddev – 出力パラメータ.求められた標準偏差
- mask – オプションである処理マスク
関数 meanStdDev は,各チャンネル毎に配列要素の平均と標準偏差を求め,それを出力パラメータに格納します:
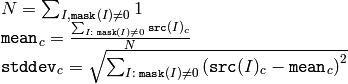
すべてのマスク要素が0の場合,この関数は Scalar::all(0) を返します.
計算される標準偏差は,完全に正規化された共分散行列の対角成分にすぎないことに注意してください.もし完全な行列が必要ならば,マルチチャンネル配列
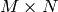 をシングルチャンネル配列
をシングルチャンネル配列
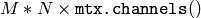 に変形して(行列が連続である場合のみ可能),この行列を
calcCovarMatrix()
に渡してください.
に変形して(行列が連続である場合のみ可能),この行列を
calcCovarMatrix()
に渡してください.
参考: countNonZero() , mean() , norm() , minMaxLoc() , calcCovarMatrix()
cv::merge¶
- void merge(const MatND* mv, size_t count, MatND& dst)
- void merge(const vector<MatND>& mv, MatND& dst)
複数のシングルチャンネル配列からマルチチャンネル配列を作成します.
パラメタ: - mv – 結合されるシングルチャンネル行列の入力配列,または入力ベクトル. mv のすべての行列は,同じサイズ,同じ型でなければいけません
- count – mv が純粋なC配列である場合の,入力行列の個数. 0より大きくなければいけません
- dst – mv[0] と同じサイズ,同じビット深度の出力配列.チャンネル数も,入力配列と一致します
関数 merge は,複数のシングルチャンネル配列を結合させて(厳密に言えば,要素をインタリーブして),1つのマルチチャンネル配列を作成します.
](_images/math/575eaf395d1f4af9ca3225e4b730c005049fb6fd.png)
関数 split() は,この逆の処理を行います.また,複数のマルチチャンネル画像を結合したり,別の高度な方法でチャンネルを入れ替える必要がある場合は, mixChannels() を利用してください.
参考: mixChannels() , split() , reshape()
cv::min¶
- Mat_Expr<...> min(const Mat& src1, double value)
- Mat_Expr<...> min(double value, const Mat& src1)
- void min(const MatND& src1, const MatND& src2, MatND& dst)
- void min(const MatND& src1, double value, MatND& dst)
2つの配列同士,あるいは配列とスカラの 要素毎の最小値を求めます.
パラメタ: - src1 – 1番目の入力配列
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- value – 実数のスカラ値
- dst – src1 と同じサイズ,同じ型である出力配列
関数 min は,2つの配列の要素を比較し大きい方を求めます:
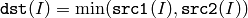
または,配列とスカラの比較:
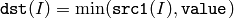
配列とスカラを引数にとる場合,入力配列がマルチチャンネルならば,各チャンネルは個別に value と比較されます.
上述したこの関数のバリエーションのうち,最初の三つの形式は,実際には Matrix Expressions の一部です.これらは行列表現オブジェクトを返します.そして,それをさらに変換したり,行列に代入したり,関数に渡したりできます.
参考: max() , compare() , inRange() , minMaxLoc() , Matrix Expressions
cv::minMaxLoc¶
- void minMaxLoc(const Mat& src, double* minVal, double* maxVal=0, Point* minLoc=0, Point* maxLoc=0, const Mat& mask=Mat())¶
- void minMaxLoc(const MatND& src, double* minVal, double* maxVal, int* minIdx=0, int* maxIdx=0, const MatND& mask=MatND())
- void minMaxLoc(const SparseMat& src, double* minVal, double* maxVal, int* minIdx=0, int* maxIdx=0)
配列全体あるいは部分配列に対する,大域的最小値および最大値を求めます.
パラメタ: - src – シングルチャンネルの入力配列
- minVal – 最小値が入る変数へのポインタ.不要ならば NULL を指定してください
- maxVal – 最大値が入る変数へのポインタ.不要ならば NULL を指定してください
- minLoc – (2次元の場合の)最小値の位置が入る変数へのポインタ.不要ならば NULL を指定してください
- maxLoc – (2次元の場合の)最大値の位置が入る変数へのポインタ.不要ならば NULL を指定してください
- minIdx – (n次元の場合の)最小値の位置が入る変数へのポインタ.不要ならば NULL を指定し,そうでなければ src.dims 要素の配列へのポインタを指定してください.そして,最小要素の各次元座標がここに格納されます
- maxIdx – (n次元の場合の)最大値の位置が入る変数へのポインタ.不要ならば NULL を指定してください
- mask – オプション:部分配列を選択する為に利用されるマスク
関数 minMaxLoc は,最小と最大の要素値,およびそれらの位置を求めます. この極値は,配列全体から探索されますが, mask が空の配列でない場合は,指定された配列領域から探索されます.
この関数は,マルチチャンネル配列に対しては動作しません.すべてのチャンネルに対する最小,最大の要素を見つける必要がある場合は,最初に reshape() を用いて配列をシングルチャンネルに再編成します.あるいは, extractImageCOI() や mixChannels() , split() などの関数を用いて,特定のチャンネルを抜き出す方法もあります.
疎な行列の場合,最小値は 0 ではない要素の中から求められます.
参考: max() , min() , compare() , inRange() , extractImageCOI() , mixChannels() , split() , reshape() .
cv::mixChannels¶
- void mixChannels(const MatND* srcv, int nsrc, MatND* dstv, int ndst, const int* fromTo, size_t npairs)
- void mixChannels(const vector<MatND>& srcv, vector<MatND>& dstv, const int* fromTo, int npairs)
入力配列の指定されたチャンネルを,出力配列の指定されたチャンネルへコピーします.
パラメタ: - srcv – 行列の入力配列,または行列の入力ベクトル.すべての行列は,同じサイズで同じビット深度でなければいけません
- nsrc – srcv の要素数
- dstv – 行列の出力配列,または行列の出力ベクトル.すべての行列は 必ず確保されていなければいけません .サイズとビット深度は srcv[0] と等くなります
- ndst – dstv の要素数
- fromTo – どのチャンネルがどこにコピーされるかを示すインデックスの組の配列. fromTo[k*2] は,0基準のインデックスであり srcv の入力チャンネルを表します.また, from_to[k*2+1] は, dstv の出力チャンネルを表すインデックスです.ここでは,連続したチャンネル番号が用いられます. つまり,1番目の入力画像チャンネルは, 0 から srcv[0].channels()-1 までのインデックスで表され,2番目の入力画像チャンネルは, channels(srcv[0].channels()) から srcv[0].channels() + srcv[1].channels()-1 までのインデックスで表されます.また,出力画像チャンネルも同様です. 特別なケースとして, from_to[k*2] が負の値の場合,対応する出力チャンネルが 0 で埋められます
- npairs – 組の個数.後者(ベクトル)の場合,このパラメターは明示的には渡されませんが, srcv.size() (= dstv.size() ) として計算できます
関数 mixChannels は,画像のチャンネルを入れ替える高度な機構を提供します. split() や merge() ,また cvtColor() のいくつかの形式は,この mixChannels の特定の場合を表しています.
例として,4チャンネル RGBA 画像を, 3チャンネル BGR 画像(つまり,R と B の交換)とアルファチャンネル画像の2つに分離するコードを示します:
Mat rgba( 100, 100, CV_8UC4, Scalar(1,2,3,4) );
Mat bgr( rgba.rows, rgba.cols, CV_8UC3 );
Mat alpha( rgba.rows, rgba.cols, CV_8UC1 );
// 行列のデータはコピーされず,ヘッダのみがコピーされるので
// 行列の配列を作成するのは非常に効率的な作業です.
Mat out[] = { bgr, alpha };
// rgba[0] -> bgr[2], rgba[1] -> bgr[1],
// rgba[2] -> bgr[0], rgba[3] -> alpha[0]
int from_to[] = { 0,2, 1,1, 2,0, 3,3 };
mixChannels( &rgba, 1, out, 2, from_to, 4 );
OpenCV の他の多くの新形式の C++ 関数と異なり(イントロダクションと Mat::create() を参照してください), mixChannels では,出力配列をあらかじめ確保しておく必要があることに注意してください.
参考: split() , merge() , cvtColor()
cv::mulSpectrums¶
- void mulSpectrums(const Mat& src1, const Mat& src2, Mat& dst, int flags, bool conj=false)¶
2つのフーリエスペクトル同士の要素毎の乗算を行います.
パラメタ: - src1 – 1番目の入力配列
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- dst – src1 と同じサイズ,同じ型である出力配列
- flags – dft() に渡されるものと同じフラグですが, DFT_ROWS だけがチェックされます
- conj – オプション.乗算の前に2番目の入力配列を共役なものに変える(真)か,変えない(偽)かを指定します
関数 mulSpectrums は,実数または複素数のフーリエ変換の結果である,CCSパック表現の行列または複素行列の要素同士の乗算を行います.
この関数は, dft() や idft() と共に,2つの配列の畳み込み( conj=false を渡す),あるいは相関( conj=false を渡す)を高速に計算するために利用されます.複素配列である場合は,単純に(要素毎に)掛け算され,また,オプションで2番目の配列を複素共役に変更できます.実数配列である場合は,CCSパック表現と仮定されます(詳しくは dft() を参照してください).
cv::multiply¶
- void multiply(const MatND& src1, const MatND& src2, MatND& dst, double scale=1)
2つの配列同士の,要素毎のスケーリングされた積を求めます.
パラメタ: - src1 – 1番目の入力配列
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- dst – src1 と同じサイズ,同じ型の出力配列
- scale – オプションであるスケールファクタ
関数 multiply は,2つの配列の各要素毎の積を求めます:
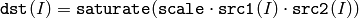
1番目の関数形式の, Matrix Expressions と相性の良いバージョンも存在します. Mat::mul() を参照してください.
要素毎の積ではなく行列の積を探しているならば, gemm() を参照してください.
参考: add() , substract() , divide() , Matrix Expressions , scaleAdd() , addWeighted() , accumulate() , accumulateProduct() , accumulateSquare() , Mat::convertTo()
cv::mulTransposed¶
- void mulTransposed(const Mat& src, Mat& dst, bool aTa, const Mat& delta=Mat(), double scale=1, int rtype=-1)¶
行列とその転置行列の積を求めます.
パラメタ: - src – 入力行列
- dst – 出力される正方行列
- aTa – 積の順序を指定します.以下の説明を参照してください
- delta – オプション.積の前に src から引かれるデルタ行列.この行列が空の場合 ( delta=Mat() ) は 0 と仮定されます.つまり,何も引かれません.そうでない場合に,これが src と同じサイズであれば単純に引き算され,サイズが異なれば src 全体をカバーするように「リピート」( repeat() を参照)されてから引き算されます.空ではないデルタ行列の型は,出力行列と同じでなければいけません. rtype の説明を参照してください
- scale – オプション.行列積に対するスケールファクタ
- rtype – これが負の値ならば,出力行列は src と同じ型になります.そうでなければ, type=CV_MAT_DEPTH(rtype) となり,これは CV_32F あるいは CV_64F です
関数 mulTransposed は, src とその転置行列の積を求めます.
aTa=true の場合は,
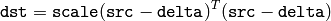
となり,そうでない場合は,
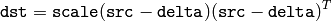
となります.この関数は,共分散行列の計算や,デルタを 0 とすることで一般的な行列積の計算の,高速な代替手段として用いられます.
参考: calcCovarMatrix() , gemm() , repeat() , reduce()
cv::norm¶
- double norm(const MatND& src1, int normType=NORM_L2, const MatND& mask=MatND())
- double norm(const MatND& src1, const MatND& src2, int normType=NORM_L2, const MatND& mask=MatND())
- double norm(const SparseMat& src, int normType)
配列の絶対値ノルム,絶対差分値ノルム,相対差分値ノルムを求めます.
パラメタ: - src1 – 1番目の入力配列
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- normType – ノルムの種類.以下の説明を参照してください
- mask – オプションである処理マスク
関数 norm は, src1 の絶対値ノルム( src2 が存在しない場合)を求めます:
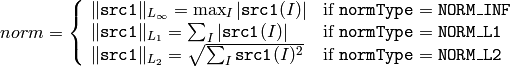
また src2 が存在する場合は,絶対差分値ノルム,相対差分値ノルムを求めます:
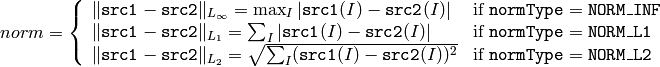
あるいは

関数 norm は,計算されたノルムを返します.
mask パラメータが存在し,それが空ではない(そして,型が CV_8U で, src1 と同じサイズ)場合,そのマスク領域によって指定された部分のノルムのみが計算されます.
マルチチャンネルの入力配列は,シングルチャンネルとして扱われます.つまり,すべてのチャンネルの結果が重ね合わされます.
cv::normalize¶
- void normalize(const Mat& src, Mat& dst, double alpha=1, double beta=0, int normType=NORM_L2, int rtype=-1, const Mat& mask=Mat())¶
- void normalize(const MatND& src, MatND& dst, double alpha=1, double beta=0, int normType=NORM_L2, int rtype=-1, const MatND& mask=MatND())
- void normalize(const SparseMat& src, SparseMat& dst, double alpha, int normType)
配列のノルム,またはその範囲を正規化します.
パラメタ: - src – 入力配列
- dst – src と同じサイズの出力配列
- alpha – ノルム正規化の場合は,正規化されるノルム値.範囲正規化の場合は,範囲の下界
- beta – ノルム正規化の場合は,不使用.範囲正規化の場合は,範囲の上界
- normType – 正規化の種類.説明を参照してください
- rtype – これが負値の場合は,出力配列の型は src と同じになり,そうでない場合は,出力配列のチャンネル数が src と等しく,ビット深度は =CV_MAT_DEPTH(rtype) となります
- mask – オプションである処理マスク
関数 normalize は,入力配列の要素にスケーリングとシフトを施し,以下を満たすようにします.
normType=NORM_INF , NORM_L1 または NORM_L2 の場合
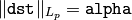
(ここで
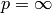 , 1 または 2)
, 1 または 2)
となり,また normType=NORM_MINMAX の場合(密な配列の場合のみ)は,
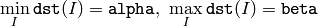
となります.
オプションのマスクは,正規化される部分配列を指定します.つまり,部分配列のノルム,または部分配列の最小値最大値が求められて,この部分配列だけが正規化されます.ノルムや最小値最大値を求める為だけにマスクを利用し,配列全体をそれで正規化したい場合は, norm() と Mat::convertScale() / MatND::convertScale() /cross{SparseMat::convertScale}を別々に利用するとよいでしょう.
疎な行列の場合,0 ではない値のみが分析され変換されます.そのため,0 基準をずらすことが出来てしまうので,疎な行列の範囲の変換はできません.
参考: norm() , Mat::convertScale() , MatND::convertScale() , SparseMat::convertScale()
PCA¶
- PCA¶
主成分分析のためのクラス.
class PCA
{
public:
// デフォルトコンストラクタ
PCA();
// 行また列データとして格納されたベクトル集合に対して PCA を行います.
PCA(const Mat& data, const Mat& mean, int flags, int maxComponents=0);
// 行また列データとして格納されたベクトル集合に対して PCA を行います.
PCA& operator()(const Mat& data, const Mat& mean, int flags, int maxComponents=0);
// ベクトルを主成分空間に射影します.
Mat project(const Mat& vec) const;
void project(const Mat& vec, Mat& result) const;
// 主成分空間への射影からベクトルを再構成します.
Mat backProject(const Mat& vec) const;
void backProject(const Mat& vec, Mat& result) const;
// 主成分空間の固有ベクトル.行列の行として格納されています.
Mat eigenvectors;
// それに対応する固有値. PCA 圧縮 / 分解では利用されません.
Mat eigenvalues;
// 平均ベクトル.射影されたベクトルから引かれます.
// または,再構成されたベクトルに足されます.
Mat mean;
};
PCA クラスは,ベクトル集合の特別な基底を求めるために利用されます.この基底は,入力ベクトル集合から計算された共分散行列の固有ベクトルで構成されます. PCA クラスは,この基底によって定義される新しい座標空間と相互にベクトルを変換することもできます.通常,この新しい座標系では,元の集合の各ベクトル(および,そのベクトルの線型結合)は,最初のいくつかの成分,つまり大きな固有値を持つ共分散行列の固有ベクトルを用いて非常に正確に近似できます.幾何的には,共分散行列の固有ベクトルのうち,影響力の大きな固有値に対応するものが張る部分空間へのベクトルの射影を計算することを意味します.そして通常,このような射影は元のベクトルに非常に近いものになります.つまり,元の高次空間のベクトルを,部分空間に射影されたベクトルの座標から成る非常に短いベクトルで表現できます.このような変換は,Karhunen-Loeve変換,KLTとしても知られています. http://en.wikipedia.org/wiki/Principal_component_analysis を参照してください.
次のサンプルは,二つの行列を引数にとる関数です.1番目の行列には,ベクトル集合が格納されており(1行が1つのベクトル),PCA の計算を行うために使われます.2番目の行列には,ベクトルの「テスト」集合が格納されており(1行が1つのベクトル),まずPCAで圧縮された後に再構成され,そこで計算された再構成誤差ノルムが各ベクトル毎に表示されます.
PCA compressPCA(const Mat& pcaset, int maxComponents,
const Mat& testset, Mat& compressed)
{
PCA pca(pcaset, // データを渡します.
Mat(), // 平均ベクトルがあらかじめ計算されているわけではないので,
// PCA の関数に計算してもらいます.
CV_PCA_DATA_AS_ROW, // ベクトルが行列の行として
// 格納されていることを示します
// (もしベクトルが列として格納されていれば
// CV_PCA_DATA_AS_COL を利用すします)
maxComponents // いくつの主成分を保持するかを指定します.
);
// テストデータが存在しなければ,計算された基底を返すだけです.
if( !testset.data )
return pca;
CV_Assert( testset.cols == pcaset.cols );
compressed.create(testset.rows, maxComponents, testset.type());
Mat reconstructed;
for( int i = 0; i < testset.rows; i++ )
{
Mat vec = testset.row(i), coeffs = compressed.row(i);
// ベクトルを圧縮し,その結果を
// 出力行列の i 番目の行に格納します.
pca.project(vec, coeffs);
// 次に,それを再構成します.
pca.backProject(coeffs, reconstructed);
// そして,誤差を計測します.
printf("
}
return pca;
}
参考: calcCovarMatrix() , mulTransposed() , SVD() , dft() , dct()
cv::PCA::PCA¶
- PCA::PCA()¶
- PCA::PCA(const Mat& data, const Mat& mean, int flags, int maxComponents=0)
PCA コンストラクタ.
パラメタ: - data – 入力サンプル.行列の行,または列として保存されています
- mean – オプション.平均値.この行列が空( Mat() )の場合,平均値はデータから計算されます
- flags –
処理フラグ.現在のところ,このパラメータはデータレイアウトを指定するためだけに利用されています
- CV_PCA_DATA_AS_ROWS 入力サンプルが,行列の行として格納されていることを示します
- CV_PCA_DATA_AS_COLS 入力サンプルが,行列の列として格納されていることを示します
- maxComponents – PCAによって残される成分の最大数.デフォルトでは,すべての成分が残されます
デフォルトコンストラクタは,空の PCA 構造体を初期化します.2番目のコンストラクタは,構造体を初期化し, PCA::operator() を呼び出します.
cv::PCA::operator ()¶
- PCA& PCA::operator()(const Mat& data, const Mat& mean, int flags, int maxComponents=0)¶
与えられたデータ集合に対して,主成分分析を行います.
パラメタ: - data – 入力サンプル.行列の行,または列として保存されています
- mean – オプション.平均値.この行列が空( Mat() )の場合,平均値はデータから計算されます
- flags –
処理フラグ.現在のところ,このパラメータはデータレイアウトを指定するためだけに利用されています
- CV_PCA_DATA_AS_ROWS 入力サンプルが,行列の行として格納されていることを示します
- CV_PCA_DATA_AS_COLS 入力サンプルが,行列の列として格納されていることを示します
- maxComponents – PCAによって保持される成分の最大数.デフォルトでは,すべての成分が保持されます
このオペレータは,与えられたデータ集合に対して PCA を実行します.同じ PCA 構造体を複数のデータ集合に対して使用しても安全です.つまり,以前に別のデータ集合に対して利用された構造体があれば,その内部データは回収され,新しい eigenvalues , eigenvectors , mean が計算されます.
求められた固有値は降順に,固有ベクトルもそれに対応するように PCA::eigenvectors の行に格納されます.
cv::PCA::project¶
- void PCA::project(const Mat& vec, Mat& result) const
(複数の)ベクトルを主成分部分空間に射影します.
パラメタ: - vec – (複数の)入力ベクトル.これらは,PCAの際の入力データと,同じ次元,同じレイアウトでなければいけません.つまり, CV_PCA_DATA_AS_ROWS が指定された場合, vec.cols==data.cols (これはベクトルの次元)であり,かつ vec.rows が射影されるベクトルの個数になります. CV_PCA_DATA_AS_COLS の場合も同様です
- result – 出力されるベクトル. CV_PCA_DATA_AS_COLS の場合を考えてみましょう.この場合,出力行列の列数は入力ベクトルの個数と同じ数,つまり, result.cols==vec.cols となり,行数は主成分数(例えば,コンストラクタに渡される maxComponents パラメータ)と一致します
このメソッドは,1つまたは複数のベクトルを主成分部分空間に射影します.各ベクトルの射影は,主成分基底の係数で表現されます.このメソッドの1番目の形式は行列を返し,2番目の形式は結果を result に書き込みます.従って,1番目の形式は式の一部として利用することができ,2番目の形式は処理ループでより効率的に実行できます.
cv::PCA::backProject¶
- void PCA::backProject(const Mat& vec, Mat& result) const
主成分空間への射影からベクトルを再構成します.
パラメタ: - vec – 主成分部分空間でのベクトルの座標.レイアウトとサイズは, PCA::project の出力ベクトルと同じです
- result – 再構成されたベクトル.レイアウトとサイズは, PCA::project の入力ベクトルと同じです
このメソッドは, PCA::project() の逆変換です.射影されたベクトルの主成分座標を引数にとり,元のベクトルを再構成します.もちろん,主成分がすべて保持されている場合を除いて,再構成されたベクトルは元のものとは異なります.しかし大抵の場合,成分数が十分に多ければ(しかし,元ベクトルの次元に比べると十分に小さいですが),その差は小さくなります.この様な理由で,PCA はよく利用されます.
cv::perspectiveTransform¶
- void perspectiveTransform(const Mat& src, Mat& dst, const Mat& mtx)¶
ベクトルの透視行列変換を行います.
パラメタ: - src – 2チャンネルまたは3チャンネル,浮動小数点型の入力配列.変換される各要素は2次元/3次元ベクトルです
- dst – src と同じサイズ,同じ型の出力行列
- mtx –
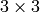 あるいは
あるいは 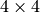 の変換行列
の変換行列
関数
perspectiveTransform
は,
src
の各要素を2次元または3次元ベクトルとして扱い,以下のように(ここでは,3次元ベクトルの変換を示します.2次元ベクトル変換の場合
 成分が除かれます)変換します:
成分が除かれます)変換します:
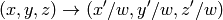
ここで
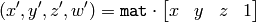
また
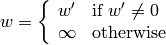
この関数は,2次元または3次元ベクトルの疎な集合を変換することに注意してください.画像を透視変換により変形したい場合は, warpPerspective() を利用します.逆の処理,つまり,いくつかの点対応の組から最も尤もらしい透視変換を求める場合は, getPerspectiveTransform() や findHomography() を利用することができます.
参考: transform() , warpPerspective() , getPerspectiveTransform() , findHomography()
cv::phase¶
- void phase(const Mat& x, const Mat& y, Mat& angle, bool angleInDegrees=false)¶
2次元ベクトルの回転角度を求めます.
パラメタ: - x – 2次元ベクトルの x 座標を表す,浮動小数点型の入力配列
- y – 2次元ベクトルの y 座標を表す,浮動小数点型の入力配列
- angle – ベクトルの角度が出力される配列. x と同じサイズ,同じ型
- angleInDegrees – これが真の場合は,角度が度単位で計算され,そうでない場合はラジアン単位で求められます
関数 phase は, x と y の対応する要素から構成される各2次元ベクトルの,回転角度を求めます:
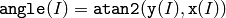
この角度の推定精度は
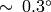 であり,
x(I)=y(I)=0
の場合,対応する
angle
(I) は
であり,
x(I)=y(I)=0
の場合,対応する
angle
(I) は
 にセットされます.
にセットされます.
参考:
cv::polarToCart¶
- void polarToCart(const Mat& magnitude, const Mat& angle, Mat& x, Mat& y, bool angleInDegrees=false)¶
2次元ベクトルの大きさと角度から,x座標,y座標を求めます.
パラメタ: - magnitude – 浮動小数点数で表される,2次元ベクトルの大きさの入力配列.空の行列( =Mat() )を渡すことも可能で,その場合は,すべての大きさが =1 であると仮定されます.空ではない場合は, angle と同じサイズ,同じ型でなければいけません
- angle – 浮動小数点数で表される,2次元ベクトルの角度の入力配列
- x – 2次元ベクトルのx座標を表す出力配列. angle と同じサイズ,同じ型
- y – 2次元ベクトルのy座標を表す出力配列. angle と同じサイズ,同じ型
- angleInDegrees – これが真の場合は,角度が度単位として扱われ,そうでない場合はラジアン単位として扱われます
関数 polarToCart は, magnitude と angle の対応する組で表される2次元ベクトルの,カーテシアン座標を求めます:
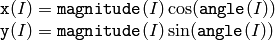
推定座標の相対精度は
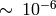 です.
です.
参考: cartToPolar() , magnitude() , phase() , exp() , log() , pow() , sqrt()
cv::pow¶
- void pow(const MatND& src, double p, MatND& dst)
各配列要素を累乗します.
パラメタ: - src – 入力配列
- p – 累乗の指数
- dst – src と同じサイズ,同じ型の出力配列
関数 pow は,入力配列の各要素を p 乗します:
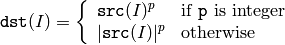
つまり,非整数の指数に対しては,入力配列要素の絶対値が用いられます.しかし,入力要素が負の場合でも,いくつか処理を追加すると正しい結果を得ることができます.以下に,配列 src の5乗根を求める例を示します:
Mat mask = src < 0;
pow(src, 1./5, dst);
subtract(Scalar::all(0), dst, dst, mask);
整数,0.5,-0.5 などのいくつかの p に対しては,特別に高速なアルゴリズムが利用されます.
参考: sqrt() , exp() , log() , cartToPolar() , polarToCart()
RNG¶
乱数生成器クラス.
class CV_EXPORTS RNG
{
public:
enum { A=4164903690U, UNIFORM=0, NORMAL=1 };
// コンストラクタ
RNG();
RNG(uint64 state);
// 32ビット符号なし乱数を返します
unsigned next();
// 指定された型の乱数を返します
operator uchar();
operator schar();
operator ushort();
operator short();
operator unsigned();
// 一様分布 [0, N) からサンプルされた整数型の乱数が返されます.
unsigned operator()(unsigned N);
unsigned operator()();
operator int();
operator float();
operator double();
// 一様分布 [a, b) からサンプルされた乱数が返されます.
int uniform(int a, int b);
float uniform(float a, float b);
double uniform(double a, double b);
// 平均が0のガウス分布乱数が返されます.
double gaussian(double sigma);
// 指定された分布からサンプルされた乱数で,配列を埋めます.
void fill( Mat& mat, int distType, const Scalar& a, const Scalar& b );
void fill( MatND& mat, int distType, const Scalar& a, const Scalar& b );
// RNG Nお内部状態(将来的に変更されるかもしれません)
uint64 state;
};
RNG クラスは,乱数生成器の実装です.これは,RNG 状態(現在は,64ビット整数)をカプセル化し,ランダムなスカラ値を返すメソッドと,乱数で配列を埋めるメソッドを持ちます.現在のところ,一様分布とガウス分布(正規分布)をサポートします.この生成器は,G. Marsaglia ( http://en.wikipedia.org/wiki/Multiply-with-carry ) によって提唱されたキャリー付き乗算アルゴリズムを利用しています.また,ガウス分布乱数は, G. Marsaglia と W. W. Tsang によって提唱された Ziggurat アルゴリズム ( http://en.wikipedia.org/wiki/Ziggurat_algorithm ) によって生成されます.
cv::RNG::RNG¶
- RNG::RNG()¶
- RNG::RNG(uint64 state)
RNG コンストラクタ
Parameter: state – RNG の初期化に利用される64ビット値
これらは RNG コンストラクタです.1番目の形式は,状態をあらかじめ定義された値,現在の実装では 2**32-1 ,にセットします.2番目の形式は,指定された値をセットします.ユーザが state=0 を引数に与えた場合,全てが0になってしまう特異な乱数列を避けるために,コンストラクタは前述のデフォルト値を代わりに利用します.
cv::RNG::operator T¶
- RNG::operator uchar() RNG::operator schar() RNG::operator ushort() RNG::operator short() RNG::operator unsigned() RNG::operator int() RNG::operator float() RNG::operator double()¶
- 次の乱数を指定された型で返します.
各メソッドは,MWC アルゴリズムを用いて状態を更新し,指定された型の次の乱数を返します.整数型の場合,戻り値は,指定された型の有効な範囲内全体から選択されます.浮動小数点数型の場合,戻り値は, [0,1) の範囲から選択されます.
cv::RNG::operator ()¶
- unsigned RNG::operator()()¶
- unsigned RNG::operator()(unsigned N)
次の乱数を返します.
Parameter: N – The upper non-inclusive boundary of the returned random number
このメソッドは,MWC アルゴリズムを用いて状態を更新し,次の乱数を返します.1番目の形式は, RNG::next() と等価です.2番目の形式は,モジュロ N の乱数,つまり [0, N) の範囲にある値を返します.
cv::RNG::uniform¶
- int RNG::uniform(int a, int b)¶
- float RNG::uniform(float a, float b)
- double RNG::uniform(double a, double b)
一様分布からサンプルされた乱数を返します.
パラメタ: - a – 返される乱数の範囲の下限(この値を含みます)
- b – 返される乱数の範囲の下限(この値を含みません)
このメソッドは,MWC アルゴリズムを用いて状態を更新し,次の一様分布乱数を返します.一様分布の範囲は [a, b) となり,乱数の型はこの引数の型から推定されます.以下の例で説明するように,それぞれ微妙な違いがあります.
cv::RNG rng;
// 常に0が生成されます
double a = rng.uniform(0, 1);
// [0, 1) 範囲の double 値が生成されます
double a1 = rng.uniform((double)0, (double)1);
// [0, 1) 範囲の float 値が生成されます
double b = rng.uniform(0.f, 1.f);
// [0, 1) 範囲の double 値が生成されます.
double c = rng.uniform(0., 1.);
// 曖昧性のためにコンパイルエラーが発生するでしょう:
// RNG::uniform(0, (int)0.999999) と RNG::uniform((double)0, 0.99999) のどっち?
double d = rng.uniform(0, 0.999999);
コンパイラは, RNG::uniform の結果に割り当てられた変数の型を考慮しません.ここで考慮されるのは,引数 a と b の型だけです.乱数の上下限値が整数値で,浮動小数点数型の乱数が欲しい場合は,引数の最後にドットをつけるか,また,定数の場合などは,上述の a1 のように明示的にキャスト演算子を利用してください.
cv::RNG::gaussian¶
- double RNG::gaussian(double sigma)¶
ガウス分布からサンプルされた乱数を返します.
Parameter: sigma – 分布の標準偏差
このメソッドは,MWC アルゴリズムを用いて状態を更新し,ガウス分布 N(0,sigma) からサンプルされた次の乱数を返します.つまり,返される乱数の平均値は0,標準偏差は sigma となります.
cv::RNG::fill¶
- void RNG::fill(MatND& mat, int distType, const Scalar& a, const Scalar& b)
配列を乱数で埋めます.
パラメタ: - mat – 2次元,またはN次元の行列.現在のところ,4チャンネルより大きなチャンネル数の行列はサポートされていません.回避策として, reshape() を利用してください
- distType – 分布の種類. RNG::UNIFORM または RNG::NORMAL
- a – 1番目の分布パラメータ.一様分布の場合,範囲の下界(この値を含みます)を表します.正規分布の場合,平均値を表します
- b – 2番目の分布パラメータ.一様分布の場合,範囲の上界(この値を含みません)を表します.正規分布の場合,標準偏差を表します
各メソッドは,指定の分布からサンプルされた乱数値で行列を埋めます.新しい値が生成されると,それに伴い RNG の状態も更新されます.マルチチャンネル画像の場合,各チャンネルは独立に埋められます.つまり,RNG は,非対角な共分散行列を持つ多次元ガウス分布から直接サンプルすることはできない,という事です.このために,まず,分布
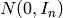 つまり,平均が0で共分散行列が単位行列となるガウス分布から行列を生成し,これを,
transform()
と個別の共分散行列を用いて変形します.
つまり,平均が0で共分散行列が単位行列となるガウス分布から行列を生成し,これを,
transform()
と個別の共分散行列を用いて変形します.
cv::randu¶
- template<typename _Tp> _Tp randu()¶
- void randu(Mat& mtx, const Scalar& low, const Scalar& high)
一様分布する乱数,または乱数の配列を生成します.
パラメタ: - mtx – 乱数の出力配列.これはあらかじめ確保されている必要があり,1から4までのチャンネルをもちます
- low – 生成される乱数の下界(範囲に含みます)
- high – 生成される乱数の上界(範囲に含みません)
関数テンプレート randu は,指定された型の一様分布する乱数を生成し,その値を返します. randu<int>() は, (int)theRNG(); などと等価です. RNG() を参照してください.
2番目の形式の関数(関数テンプレートではない方)は,指定された範囲内で一様分布する乱数で行列 mtx を埋めます:
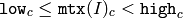
cv::randn¶
- void randn(Mat& mtx, const Scalar& mean, const Scalar& stddev)¶
正規分布する乱数で配列を埋めます.
パラメタ: - mtx – 乱数の出力配列.これはあらかじめ確保されている必要があり,1から4までのチャンネルをもちます
- mean – 生成される乱数の平均値(期待値)
- stddev – 生成される乱数の標準偏差
関数 randn は,指定された平均と標準偏差で正規分布する乱数を生成し,行列 mtx をそれで埋めます.生成された数値には が適用されます(つまり,値が切り詰められます).
参考: RNG() , randu()
cv::randShuffle¶
- void randShuffle(Mat& mtx, double iterFactor=1., RNG* rng=0)¶
配列の要素をランダムに入れ替えます.
パラメタ: - mtx – 入力と出力に利用される1次元の数値配列
- iterFactor – 入れ替え処理の回数を決めるスケールファクタ.説明を参照してください
- rng – オプション.入れ替えに利用される乱数生成器.これが 0 ならば,代わりに theRNG() () が利用されます
関数 randShuffle は,指定された1次元配列の要素をランダムに選択し,それらを入れ替えることでシャッフルを行います.このような入れ替え処理は, mtx.rows*mtx.cols*iterFactor 回行われます.
参考: RNG() , sort()
cv::reduce¶
- void reduce(const Mat& mtx, Mat& vec, int dim, int reduceOp, int dtype=-1)¶
行列をベクトルに縮小します.
パラメタ: - mtx – 2次元の入力行列
- vec – 出力ベクトル.サイズと型は,パラメータ dim と dtype によって決められます
- dim – 行列が縮小される際に従う次元インデックス.0 は行列が1行 に,1 は行列が1列に縮小されることをそれぞれ意味します
- reduceOp –
縮小処理,以下のうちの1つ:
- CV_REDUCE_SUM 出力は,行列の行(または列)の合計
- CV_REDUCE_AVG 出力は,行列の行(または列)の平均
- CV_REDUCE_MAX 出力は,行列の行(または列)の最大値
- CV_REDUCE_MIN 出力は,行列の行(または列)の最小値
- dtype – これが負の場合,出力ベクトルは入力行列と同じ型です.そうでない場合,型は CV_MAKE_TYPE(CV_MAT_DEPTH(dtype), mtx.channels()) となります
関数 reduce は,行列の行または列を1次元ベクトルの集合として扱い,単一の行または列が得られるまで,そのベクトル集合に対して指定された処理を繰り返します.例えば,ラスタ画像を水平軸や垂直軸に射影する場合に,この関数が利用できます. CV_REDUCE_SUM および CV_REDUCE_AVG の場合は,計算精度を保つために(桁溢れしないように),出力ベクトル要素のビット深度を入力よりも大きくとるべきです.また,これら2つの縮小モードの場合は,マルチチャンネル画像を扱うこともできます.
参考: repeat()
cv::repeat¶
- Mat repeat(const Mat& src, int ny, int nx)
入力配列を繰り返しコピーして出力配列を埋めます.
パラメタ: - src – 複製される入力配列
- dst – src と同じ型の出力配列
- ny – src が垂直方向に繰り返される回数
- nx – src が水平方向に繰り返される回数
関数 repeat() は,2つの軸それぞれに沿って,入力配列を1回または複数回複製します:
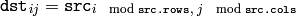
2番目の形式の関数は, Matrix Expressions と一緒に利用する際に便利です.
参考: reduce() , Matrix Expressions
cv::saturate_cast¶
- template<typename _Tp> inline _Tp saturate_cast(unsigned char v)¶
- template<typename _Tp> inline _Tp saturate_cast(signed char v)
- template<typename _Tp> inline _Tp saturate_cast(unsigned short v)
- template<typename _Tp> inline _Tp saturate_cast(signed short v)
- template<typename _Tp> inline _Tp saturate_cast(int v)
- template<typename _Tp> inline _Tp saturate_cast(unsigned int v)
- template<typename _Tp> inline _Tp saturate_cast(float v)
- template<typename _Tp> inline _Tp saturate_cast(double v)
ある基本型から別の基本型への正確な変換のためのテンプレート関数.
Parameter: v – この関数のパラメータ
関数 saturate_cast は, static_cast<T>() などの C++ の標準的なキャスト操作と似ています.これらは,ある基本型から別の基本型へ効率的に,かつ正確に変換を行います.詳しくは,イントロダクションを参照してください.名前の “saturate” は,入力値 v が変換後の型の範囲外にある場合に,単に入力の下位ビットを持ってくるわけではなく,代わりに数値を切り詰めることを意味します.例えば:
uchar a = saturate_cast<uchar>(-100); // a = 0 (UCHAR_MIN)
short b = saturate_cast<short>(33333.33333); // b = 32767 (SHRT_MAX)
このような切り詰めは,変換後の型が unsigned char, signed char, unsigned short, signed short である場合に起こります.32 ビット整数に対しては切り詰めは行われません.
パラメータが浮動小数点数であり,変換後の型が整数(8ビット,16ビット,32ビット)である場合,この浮動小数点数は,まず最も近い整数値に丸められてから,必要ならば切り詰められます(変換後の型が,8ビットあるいは16ビット整数の場合).
この処理は,OpenCV のほとんどの画像処理関数で利用されています.
参考: add() , subtract() , multiply() , divide() , Mat::convertTo()
cv::scaleAdd¶
- void scaleAdd(const MatND& src1, double scale, const MatND& src2, MatND& dst)
スケーリングされた配列と別の配列との和を求めます.
パラメタ: - src1 – 1番目の入力配列
- scale – 1番目の配列に対するスケールファクタ
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- dst – src1 と同じサイズ,同じ型になる出力配列
関数 cvScaleAdd は, BLAS における DAXPY あるいは SAXPY として知られる,線形代数の古典的な基本処理の1つです.これは,スケーリングされた配列と別の配列との和を求めます.
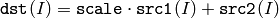
行列表現を用いて,この関数と同じ処理をすることもできます.例えば:
Mat A(3, 3, CV_64F);
...
A.row(0) = A.row(1)*2 + A.row(2);
参考: add() , addWeighted() , subtract() , Mat::dot() , Mat::convertTo() , Matrix Expressions
cv::setIdentity¶
- void setIdentity(Mat& dst, const Scalar& value=Scalar(1))¶
行列を,定数倍した単位行列として初期化します.
パラメタ: - dst – 初期化される行列(正方である必要はありません)
- value – 対角要素に代入される値
関数 setIdentity() は,行列を,定数倍した単位行列として初期化します:
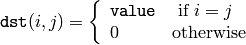
行列の初期化と行列表現を用いて,この関数と同じ処理をすることもできます.例えば:
Mat A = Mat::eye(4, 3, CV_32F)*5;
// A には [[5, 0, 0], [0, 5, 0], [0, 0, 5], [0, 0, 0]] がセットされます.
参考: Mat::zeros() , Mat::ones() , Matrix Expressions ,
Mat::setTo() , Mat::operator=() ,
cv::solve¶
- bool solve(const Mat& src1, const Mat& src2, Mat& dst, int flags=DECOMP_LU)¶
連立一次方程式,あるいは最小二乗問題を解きます.
パラメタ: - src1 – 連立方程式の左辺の入力行列
- src2 – 連立方程式の右辺の入力行列
- dst – 出力される解
- flags –
解(逆行列)を求める手法
- DECOMP_LU 最適なピボット選択を行うガウスの消去法
- DECOMP_CHOLESKY コレスキー
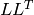 因数分解.行列 src1 は対称でなければいけません
因数分解.行列 src1 は対称でなければいけません - DECOMP_EIG 固有値分解.行列 src1 は対称でなければいけません
- DECOMP_SVD 特異値分解(SVD).連立方程式が優決定,かつ/あるいは, src1 が特異行列でも構いません
- DECOMP_QR QR 因数分解.連立方程式が優決定,かつ/あるいは, src1 が特異行列でも構いません
- DECOMP_NORMAL これまでのフラグは排他的にしか利用できませんが,これは上述のフラグの1つと同時に利用できます.この場合,元の連立方程式
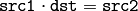 の代わりに,正規方程式
の代わりに,正規方程式 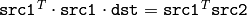 が解かれます
が解かれます
関数 solve は,連立方程式あるいは最小二乗問題を解きます(後者は,SVD か QR メソッド,または DECOMP_NORMAL フラグを指定して解くことができます).
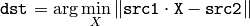
DECOMP_LU
あるいは
DECOMP_CHOLESKY
メソッドが用いられる場合,
src1
(または
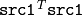 )が正則ならば1を返し,そうでなければ0を返します.後者の場合,
drt
は無効になります.別のメソッドが用いられる場合,左辺が特異行列ならば擬似逆行列を求めます.
)が正則ならば1を返し,そうでなければ0を返します.後者の場合,
drt
は無効になります.別のメソッドが用いられる場合,左辺が特異行列ならば擬似逆行列を求めます.
劣決定の連立方程式
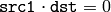 において単一の解を求めたい場合は,関数
solve
は使えません.代わりに
SVD::solveZ()
を利用してください.
において単一の解を求めたい場合は,関数
solve
は使えません.代わりに
SVD::solveZ()
を利用してください.
cv::solveCubic¶
- void solveCubic(const Mat& coeffs, Mat& roots)¶
三次方程式の実根を求める.
パラメタ: - coeffs – 3個あるいは4個の値をもつ,方程式の係数配列
- roots – 実根の出力配列,3個の要素をもちます
関数 solveCubic は,三次方程式の実根を求めます:
coeffs が4要素ベクトルの場合:
![\texttt{coeffs} [0] x^3 + \texttt{coeffs} [1] x^2 + \texttt{coeffs} [2] x + \texttt{coeffs} [3] = 0](_images/math/fe7795e1b29e8f68c0ede218705289b0674bba6b.png)
coeffs が3要素ベクトルの場合:
![x^3 + \texttt{coeffs} [0] x^2 + \texttt{coeffs} [1] x + \texttt{coeffs} [2] = 0](_images/math/ba956f7c22249ea7674f92cbab534fde659bd964.png)
実根は,配列 roots に格納されます.
cv::solvePoly¶
- void solvePoly(const Mat& coeffs, Mat& roots, int maxIters=20, int fig=100)¶
Finds the real or complex roots of a polynomial equation
パラメタ: - coeffs – 多項式の係数配列
- roots – 出力される(複素)根の配列
- maxIters – アルゴリズムの最大反復回数
- fig –
関数 solvePoly は,多項式の実根または複素根を求めます:
![\texttt{coeffs} [0] x^{n} + \texttt{coeffs} [1] x^{n-1} + ... + \texttt{coeffs} [n-1] x + \texttt{coeffs} [n] = 0](_images/math/4f9145a6bf4b86458d848c045e6e861b943164ee.png)
cv::sort¶
- void sort(const Mat& src, Mat& dst, int flags)¶
行列の各行,または各列をソートします.
パラメタ: - src – シングルチャンネルの入力配列
- dst – src と同じサイズ,同じ型の出力配列
- flags –
処理フラグ.以下の値の組み合わせ:
- CV_SORT_EVERY_ROW 行列の各行が独立にソートされます
- CV_SORT_EVERY_COLUMN 行列の各列が独立にソートされます.このフラグは,前述のフラグとは排他的にしか利用できません
- CV_SORT_ASCENDING 行列の各行は昇順にソートされます
- CV_SORT_DESCENDING 行列の各行は降順にソートされます.このフラグは,前述のフラグとは排他的にしか利用できません
関数 sort は,行列の各行または各列を,昇順または降順にソートします.行列の各行または各列を辞書順にソートしたい場合は,適切な比較述語を渡した STL の汎用関数 std::sort を利用してください.
参考: sortIdx() , randShuffle()
cv::sortIdx¶
- void sortIdx(const Mat& src, Mat& dst, int flags)¶
行列の各行,または各列をソートします.
パラメタ: - src – シングルチャンネルの入力配列
- dst – src と同じサイズ,同じ型の出力配列
- flags –
処理フラグ.以下の値の組み合わせ:
- CV_SORT_EVERY_ROW 行列の各行が独立にソートされます
- CV_SORT_EVERY_COLUMN 行列の各列が独立にソートされます.このフラグは,前述のフラグとは排他的にしか利用できません
- CV_SORT_ASCENDING 行列の各行は昇順にソートされます
- CV_SORT_DESCENDING 行列の各行は降順にソートされます.このフラグは,前述のフラグとは排他的にしか利用できません
関数 sortIdx は,行列の各行または各列を,昇順または降順にソートします.要素自身を並べ換える代わりに,ソートされた要素のインデックスが出力配列に格納されます.例えば:
Mat A = Mat::eye(3,3,CV_32F), B;
sortIdx(A, B, CV_SORT_EVERY_ROW + CV_SORT_ASCENDING);
// B はおそらく次のようになります.
// ( A に同値の要素があると,その入れ替わりが起こる可能性があるので)
// [[1, 2, 0], [0, 2, 1], [0, 1, 2]]
参考: sort() , randShuffle()
cv::split¶
- void split(const MatND& mtx, MatND* mv)
- void split(const MatND& mtx, vector<MatND>& mv)
マルチチャンネルの配列を,複数のシングルチャンネルの配列に分割します.
パラメタ: - mtx – マルチチャンネルの入力配列
- mv – 出力配列,または出力ベクトルの配列.配列の数は, mtx.channels() と一致しなければいけません.この配列自身は,必要ならば再割り当てされます
関数 split は,マルチチャンネルの配列を,別々のシングルチャンネルの配列に分割します:
 = \texttt{mtx} (I)_c](_images/math/740b13e20b007684a7ae0d8599855a9053551b1f.png)
シングルチャンネルの抽出,またはより洗練されたチャンネルの入れ替えが必要ならば, mixChannels() を利用してください.
参考: merge() , mixChannels() , cvtColor()
cv::sqrt¶
- void sqrt(const MatND& src, MatND& dst)
配列要素の平方根を求めます.
パラメタ: - src – 浮動小数点型の入力配列
- dst – src と同じサイズ,同じ型の出力配列
関数 sqrt は,入力配列の各要素の平方根を求めます.マルチチャンネル配列の場合,各チャンネルは個別に処理されます.この関数の精度は,組み込みの std::sqrt と同等です.
参考: pow() , magnitude()
cv::subtract¶
- void subtract(const MatND& src1, const MatND& src2, MatND& dst)
- void subtract(const MatND& src1, const MatND& src2, MatND& dst, const MatND& mask)
- void subtract(const MatND& src1, const Scalar& sc, MatND& dst, const MatND& mask=MatND())
- void subtract(const Scalar& sc, const MatND& src2, MatND& dst, const MatND& mask=MatND())
2つの配列同士,あるいは配列とスカラの 要素毎の差を求めます.
パラメタ: - src1 – 1番目の入力配列
- src2 – src1 と同じサイズ,同じ型である2番目の入力配列
- sc – スカラ.1番目または2番目の入力パラメータ
- dst – src1 と同じサイズ,同じ型の出力配列. Mat::create を参照してください
- mask – オプション.8ビット,シングルチャンネル配列の処理マスク.出力配列内の変更される要素を表します
関数 subtract は,以下を求めます:
2つの配列同士の差:
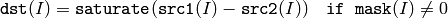
配列とスカラの差:
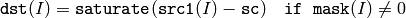
スカラと配列の差:
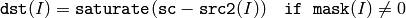
ここで I は,配列要素の多次元インデックスを表します.
上述のリストの最初の関数は,行列表現を用いたもので置き換えることができます:
dst = src1 - src2;
dst -= src2; // subtract(dst, src2, dst); と等価
参考: add() , addWeighted() , scaleAdd() , convertScale() , Matrix Expressions , .
SVD¶
- SVD¶
特異値分解を行うためのクラス.
class SVD
{
public:
enum { MODIFY_A=1, NO_UV=2, FULL_UV=4 };
// デフォルトコンストラクタ
SVD();
// A を u, w, vt に分解します: A = u*w*vt;
// u と vt は直行行列, w は 対角行列です
SVD( const Mat& A, int flags=0 );
// A を u, w, vt に分解します.
SVD& operator ()( const Mat& A, int flags=0 );
// A が特異行列の場合に, A*x = 0 かつ,
// norm(x)=1 を満たす x を求めます.
static void solveZ( const Mat& A, Mat& x );
// 後退代入を行います:
// x = vt.t()*inv(w)*u.t()*rhs ~ inv(A)*rhs
void backSubst( const Mat& rhs, Mat& x ) const;
Mat u, w, vt;
};
SVD クラスは,最小二乗問題,劣決定連立方程式,逆行列,条件数の計算などの解を得るための,浮動小数点型行列の特異値分解を行うために利用されます.
分解される行列を保存しておく必要がなければ, flags=SVD::MODIFY_A|... を渡して行列を直接変更すると,処理が少し速くなります.行列の条件数や行列式の絶対値を求めたい場合は, u と vt は不要なので flags=SVD::NO_UV|... を渡しても構いません.もう1つのフラグ FULL_UV は,完全なサイズの u と vt を必ず求めることを指定しますが,これは大抵の場合は不要です.
参考: invert() , solve() , eigen() , determinant()
cv::SVD::SVD¶
- SVD::SVD()¶
- SVD::SVD(const Mat& A, int flags=0)
SVD コンストラクタ
パラメタ: - A – 分解される行列
- flags –
処理フラグ
- SVD::MODIFY_A このアルゴリズムは,分解される行列を変更します.メモリの節約され,わずかに速度が向上します
- SVD::NO_UV 特異値だけを求めます.このアルゴリズムは,行列 U と V を計算しません
- SVD::FULL_UV 行列が正方でない場合,このアルゴリズムはデフォルトで, A を再構成するのに十分なサイズの行列 U と V を生成します.しかし,この FULL_UV フラグが指定された場合は, U と V はフルサイズの正方な直行行列になります
1番目のコンストラクタは,空の SVD 構造体を初期化します.2番目のコンストラクタは,空の SVD 構造体を初期化し, SVD::operator () を呼び出します.
cv::SVD::operator ()¶
- SVD& SVD::operator()( const Mat& A, int flags=0)¶
行列の特異値分解を行います.
パラメタ: - A – 分解される行列
- flags –
処理フラグ
- SVD::MODIFY_A このアルゴリズムは,分解される行列を変更します.メモリの節約され,わずかに速度が向上します
- SVD::NO_UV 特異値だけを求めます.このアルゴリズムは,行列 U と V を計算しません
- SVD::FULL_UV 行列が正方でない場合,このアルゴリズムはデフォルトで, A を再構成するのに十分なサイズの行列 U と V を生成します.しかし,この FULL_UV フラグが指定された場合は, U と V はフルサイズの正方な直行行列になります
このオペレータは,与えられた行列を特異値分解します. U ,転置された V , W の対角成分,が構造体に格納されます.また,同じ SVD 構造体を,異なる行列に対して再利用することができます.もし必要ならば,以前の u , vt , w は回収され,新しい行列が作成されます.これらはすべて Mat::create() によって実現されます.
cv::SVD::solveZ¶
このメソッドは,劣決定連立方程式
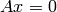 の単位長さの解
x
を求めます.この様な方程式は,理論的には無限個の解を持つので,このアルゴリズムでは,最小の特異値(0のはず)に対応する右特異ベクトルを単位長さの解として求めます.実際には,丸め誤差や,浮動小数点数の精度限界により,入力行列は完全な特異行列ではなく,特異行列に近い行列とみなされます.よって,厳密に言えば,このアルゴリズムは以下の問題を解くことになります:
の単位長さの解
x
を求めます.この様な方程式は,理論的には無限個の解を持つので,このアルゴリズムでは,最小の特異値(0のはず)に対応する右特異ベクトルを単位長さの解として求めます.実際には,丸め誤差や,浮動小数点数の精度限界により,入力行列は完全な特異行列ではなく,特異行列に近い行列とみなされます.よって,厳密に言えば,このアルゴリズムは以下の問題を解くことになります:
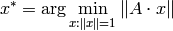
cv::SVD::backSubst¶
- void SVD::backSubst(const Mat& rhs, Mat& x) const¶
特異値後退代入を行います.
パラメタ: - rhs – 連立方程式
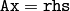 の右辺.ここで A は, SVD::SVD() または SVD::operator () に渡される行列です
の右辺.ここで A は, SVD::SVD() または SVD::operator () に渡される行列です - x – 連立方程式の解
- rhs – 連立方程式
このメソッドは,指定された右辺に対して後退代入を行います.
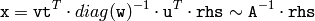
この方法を用いることで,連立方程式の非常に正確な解,または優決定連立方程式の(二乗誤差の意味で)最良の擬似解を得ることができます.同じ左辺(例えば, A )を持つ連立方程式を大量に解く必要があるならば,後退代入を行う SVD を明示的に利用することが唯一の方法です.単一の連立方程式(あるいは,複数の rhs が即得られるようなもの)を解くだけならば,単に solve() を呼び出して,そこに cv::DECOMP_SVD を渡せばよく,これはまったく同じ事です.
cv::sum¶
- Scalar sum(const MatND& mtx)
配列要素の和を求めます.
Parameter: mtx – 1から4までのチャンネルを持つ入力配列
関数 sum は,各チャンネル毎の配列要素の和を求め,それを返します.
参考: countNonZero() , mean() , meanStdDev() , norm() , minMaxLoc() , reduce()
cv::theRNG¶
- RNG& theRNG()¶
- デフォルトの乱数生成器を返します.
関数 theRNG は,デフォルトの乱数生成器を返します.各スレッド毎に別の乱数生成機が存在するので,この関数はマルチスレッド環境でも安全に利用できます.この生成器から発生する乱数が1つだけ必要な場合,あるいは配列を初期化する必要がある場合は,代わりに randu() や randn() が利用できます.しかし,ループ内で多くの乱数を生成するならば,この関数を用いて生成器を取得した後に RNG::operator _Tp() を利用した方がはるかに高速です.
cv::transform¶
- void transform(const Mat& src, Mat& dst, const Mat& mtx)¶
各配列要素の変換を行います.
パラメタ: - src – mtx.cols あるいは mtx.cols-1 と同数のチャンネル(1から4)を持つ入力配列
- dst – src と同じサイズ,同じビット深度で, mtx.rows と同数のチャンネルを持つ出力配列
- mtx – 変換行列
関数 transform は,配列 src の各要素に対して行列変換を行い,その結果を dst に格納します.
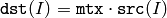
(ここで mtx.cols=src.channels() ),または
![\texttt{dst} (I) = \texttt{mtx} \cdot [ \texttt{src} (I); 1]](_images/math/6ab1892bca72c46d76adb03974a871c527834112.png)
(ここで mtx.cols=src.channels()+1 )
つまり,
N
-チャンネル配列
src
の各要素は,
N
-要素のベクトルとみなされます.そしてこれらは,
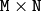 または
または
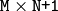 の行列
mtx
によって,
M
-チャンネル配列
dst
に変換されます.
の行列
mtx
によって,
M
-チャンネル配列
dst
に変換されます.
この関数は,
 -次元点の幾何学変換,色空間の任意の(様々な RGB
-次元点の幾何学変換,色空間の任意の(様々な RGB
 YUV 変換のような)線形変換,画像チャンネルの入れ替え,などにも利用されます.
YUV 変換のような)線形変換,画像チャンネルの入れ替え,などにも利用されます.
参考: perspectiveTransform() , getAffineTransform() , estimateRigidTransform() , warpAffine() , warpPerspective()
ヘルプとフィードバック
お探しの情報が見つかりませんか?- FAQ (英語)を試してください.
- ユーザグループ/メーリングリスト (英語)で質問してみてください.
- このドキュメントに誤りなどを見つけたらbug report まで報告してください.また,日本語訳に関する誤りや指摘はopencv.jpまでお願い します.