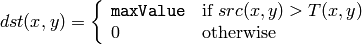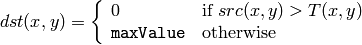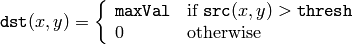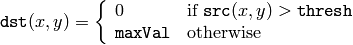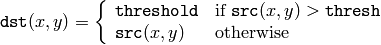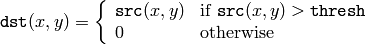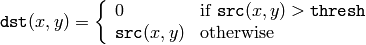その他の画像変換¶
cv::adaptiveThreshold¶
- void adaptiveThreshold(const Mat& src, Mat& dst, double maxValue, int adaptiveMethod, int thresholdType, int blockSize, double C)¶
配列に対して,適応的な閾値処理を行います.
パラメタ: - src – 8ビット,シングルチャンネルの入力画像
- dst – src と同じサイズ,同じタイプの出力画像
- maxValue – 条件を満足するピクセルに割り当てられる非0の値.説明を参照してください
- adaptiveMethod – 利用される適応的閾値アルゴリズム: ADAPTIVE_THRESH_MEAN_C または ADAPTIVE_THRESH_GAUSSIAN_C (説明を参照してください)
- thresholdType – 閾値の種類. THRESH_BINARY または THRESH_BINARY_INV のどちらか
- blockSize – ピクセルの閾値を求めるために利用される近傍領域のサイズ.3, 5, 7, など
- C – 平均または加重平均から引かれる定数(説明を参照).通常,これは正値ですが,0や負値の可能性もあります
関数 adaptiveThreshold は,以下の式にしたがってグレースケール画像を2値画像に変換します:
THRESH_BINARY
THRESH_BINARY_INV
ここで
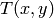 は,個々のピクセルに対して求められる閾値です.
は,個々のピクセルに対して求められる閾値です.
- ADAPTIVE_THRESH_MEAN_C
メソッドの場合,閾値
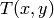 は,
は,
 の近傍
の近傍
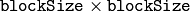 の平均から
C
を引いた値になります.
の平均から
C
を引いた値になります. - ADAPTIVE_THRESH_GAUSSIAN_C
メソッドの場合,閾値
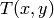 は,
は,
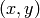 の近傍
の近傍
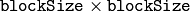 の加重平均(つまり,ガウシアン窓による相互相関)から
C
を引いた値になります.デフォルトのシグマ(標準偏差)は,指定された
blockSize
から求められます.
getGaussianKernel()
を参照してください.
の加重平均(つまり,ガウシアン窓による相互相関)から
C
を引いた値になります.デフォルトのシグマ(標準偏差)は,指定された
blockSize
から求められます.
getGaussianKernel()
を参照してください.
この関数は,置換モードでも動作します.
参考: threshold() , blur() , GaussianBlur()
cv::cvtColor¶
- void cvtColor(const Mat& src, Mat& dst, int code, int dstCn=0)¶
画像の色空間を変換します.
パラメタ: - src – 8ビット符号なし整数型,16ビット符号なし整数型( CV_16UC... ),または単精度浮動小数型の入力画像
- dst – src と同じサイズ,同じタイプの出力画像
- code – 色空間の変換コード.説明を参照してください
- dstCn – 出力画像のチャンネル数.この値が 0 の場合,チャンネル数は src と code から自動的に求められます
関数 cvtColor は,入力画像の色空間を別の色空間に変換します.RGB 色空間との相互変換の場合,チャンネルの順序を明示的に指定する必要があります(RGB あるいは BGR).
R, G, B チャンネルの値の標準的な範囲は,以下のようになります:
- CV_8U 画像の場合,0 から 255
- CV_16U 画像の場合,0 から 65535
- CV_32F 画像の場合,0 から 1
もちろん,線形変換の場合は,この範囲は問題にいけません.しかし,RGB
 L*u*v* 変換のような非線形変換の場合,RGB入力画像を適切な範囲にある値に正規化しなければいけません.例えば,8ビット画像をスケーリングなしで32ビット浮動小数点型画像に変換すると,この関数では0から1の範囲を仮定しているにも関わらず,実際には0から1の範囲の値になります.したがって,
cvtColor
を呼ぶ前に,まず画像をスケーリングする必要があります:
L*u*v* 変換のような非線形変換の場合,RGB入力画像を適切な範囲にある値に正規化しなければいけません.例えば,8ビット画像をスケーリングなしで32ビット浮動小数点型画像に変換すると,この関数では0から1の範囲を仮定しているにも関わらず,実際には0から1の範囲の値になります.したがって,
cvtColor
を呼ぶ前に,まず画像をスケーリングする必要があります:
img *= 1./255;
cvtColor(img, img, CV_BGR2Luv);
この関数では,以下の変換が可能です:
RGB 空間内での変換,アルファチャンネルの追加や削除,チャンネル順序の反転,16ビットRGBカラー(R5:G6:B5 または R5:G5:B5)との相互変換,グレースケールとの相互変換.これには,以下の式を利用します:
![\text{RGB[A] to Gray:} \quad Y \leftarrow 0.299 \cdot R + 0.587 \cdot G + 0.114 \cdot B](_images/math/aec60f2c1832bb07ad040335189257e97afd00d6.png)
と
![\text{Gray to RGB[A]:} \quad R \leftarrow Y, G \leftarrow Y, B \leftarrow Y, A \leftarrow 0](_images/math/8f5c51f3a4cae34d417208c8f561b2b5e264dc41.png)
RGB画像からグレースケールへの変換は,次のようになります:
cvtColor(src, bwsrc, CV_RGB2GRAY);
より高度なチャンネル順序の変更は, mixChannels を利用して行うことができます.
RGB
 CIE XYZ ,Rec 709仕様,D65 白色点 (
CV_BGR2XYZ, CV_RGB2XYZ, CV_XYZ2BGR, CV_XYZ2RGB
):
CIE XYZ ,Rec 709仕様,D65 白色点 (
CV_BGR2XYZ, CV_RGB2XYZ, CV_XYZ2BGR, CV_XYZ2RGB
):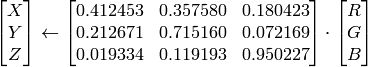
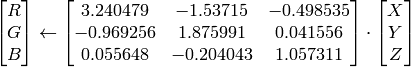
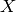 ,
,
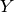 および
および
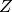 は,全範囲をカバーします(浮動小数点型の画像の場合,
は,全範囲をカバーします(浮動小数点型の画像の場合,
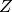 は1を越える可能性があります).
は1を越える可能性があります).RGB
 YCrCb JPEG (YCCとも呼ばれます) (
CV_BGR2YCrCb, CV_RGB2YCrCb, CV_YCrCb2BGR, CV_YCrCb2RGB
)
YCrCb JPEG (YCCとも呼ばれます) (
CV_BGR2YCrCb, CV_RGB2YCrCb, CV_YCrCb2BGR, CV_YCrCb2RGB
)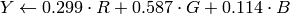
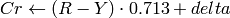
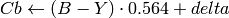
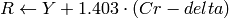
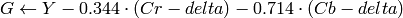
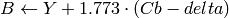
ここで,
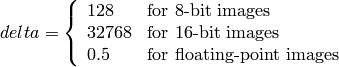
Y, Cr および Cb は,全範囲をカバーします.
RGB
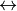 HSV (
CV_BGR2HSV, CV_RGB2HSV, CV_HSV2BGR, CV_HSV2RGB
)
HSV (
CV_BGR2HSV, CV_RGB2HSV, CV_HSV2BGR, CV_HSV2RGB
)8ビット および 16ビット画像の場合,R, G, B は浮動小数点型のフォーマットに変換され,0から1の範囲に収まるようにスケーリングされます.
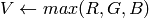
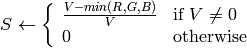
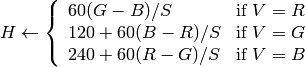
もし
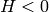 ならば
ならば
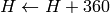 出力値の範囲は,
出力値の範囲は,
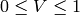 ,
,
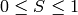 ,
,
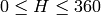 .
.これらの値は,出力されるべき型に変換されます:
8ビット画像
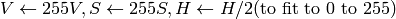
- 16ビット画像
現在はサポートされていません
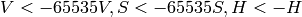
- 32ビット画像
H, S, V は,そのまま
RGB
 HLS (
CV_BGR2HLS, CV_RGB2HLS, CV_HLS2BGR, CV_HLS2RGB
).
HLS (
CV_BGR2HLS, CV_RGB2HLS, CV_HLS2BGR, CV_HLS2RGB
).8ビット および 16ビット画像の場合,R, G, B は浮動小数点型のフォーマットに変換され,0から1の範囲に収まるようにスケーリングされます.
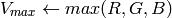
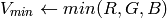
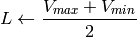
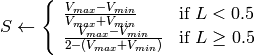
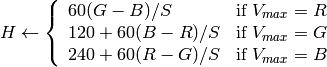
if
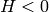 then
then
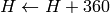 出力の範囲は,
出力の範囲は,
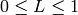 ,
,
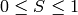 ,
,
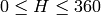 .
.これらの値は,出力されるべき型に変換される:
8ビット画像
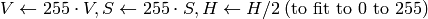
- 16ビット画像
現在はサポートされていません
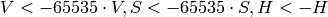
- 32ビット画像
H, S, V は,そのまま
RGB
 CIE L*a*b* (
CV_BGR2Lab, CV_RGB2Lab, CV_Lab2BGR, CV_Lab2RGB
)
CIE L*a*b* (
CV_BGR2Lab, CV_RGB2Lab, CV_Lab2BGR, CV_Lab2RGB
)8ビット および 16ビット画像の場合,R, G, B は浮動小数点型のフォーマットに変換され,0から1の範囲に収まるようにスケーリングされます.
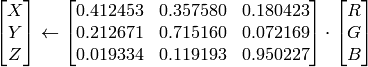
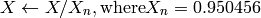
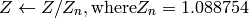
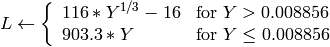
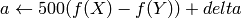
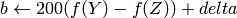
ここで,
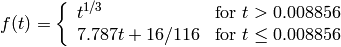
および
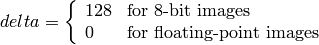
出力の範囲は,
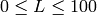 ,
,
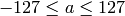 ,
,
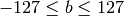 これらの値は,出力されるべき型に変換されます:
これらの値は,出力されるべき型に変換されます:8ビット画像
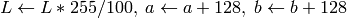
- 16ビット画像
現在はサポートされていません
- 32ビット画像
L, a, b は,そのまま
RGB
 CIE L*u*v* (
CV_BGR2Luv, CV_RGB2Luv, CV_Luv2BGR, CV_Luv2RGB
)
CIE L*u*v* (
CV_BGR2Luv, CV_RGB2Luv, CV_Luv2BGR, CV_Luv2RGB
)8ビット および 16ビット画像の場合,R, G, B は浮動小数点型のフォーマットに変換され,0から1の範囲に収まるようにスケーリングされます.
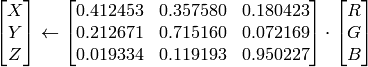
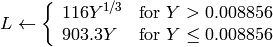
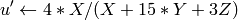
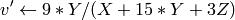

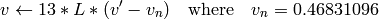
出力の範囲は,
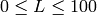 ,
,
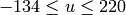 ,
,
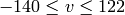 .
.これらの値は,出力されるべき型に変換されます:
8ビット画像
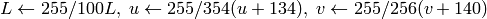
- 16ビット画像
現在はサポートされていません
- 32ビット画像
L, u, v は,そのまま
上に示したRGBと各種の色空間との変換式は,Web上の複数の情報を参考にしています.特に Charles Poynton のサイト http://www.poynton.com/ColorFAQ.html からは多くの情報を得ました.
Bayer
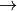 RGB (
CV_BayerBG2BGR, CV_BayerGB2BGR, CV_BayerRG2BGR, CV_BayerGR2BGR, CV_BayerBG2RGB, CV_BayerGB2RGB, CV_BayerRG2RGB, CV_BayerGR2RGB
) Bayer パターンは,CCD カメラや CMOS カメラなどで広く利用されています.R,G,B の各ピクセル(ある特定のセンサ)が次ように交互に配置された1つのプレーンから,カラー画像を得ることができます.
RGB (
CV_BayerBG2BGR, CV_BayerGB2BGR, CV_BayerRG2BGR, CV_BayerGR2BGR, CV_BayerBG2RGB, CV_BayerGB2RGB, CV_BayerRG2RGB, CV_BayerGR2RGB
) Bayer パターンは,CCD カメラや CMOS カメラなどで広く利用されています.R,G,B の各ピクセル(ある特定のセンサ)が次ように交互に配置された1つのプレーンから,カラー画像を得ることができます.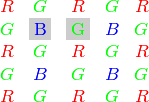
出力される各ピクセルのRGB値は,同色のピクセルの 1隣接,2隣接 あるいは4隣接を用いた補間により求められます. 上述のパターンには,いくつかのバリエーションが存在します.それらは,パターンを1ピクセルだけ左にシフト,さらに(あるいは)1ピクセルだけ上にシフトすることで得られます. また,変換定数
CV_Bayer
 2BGR
と
2BGR
とCV_Bayer
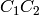 2RGB
に現れる2つの文字
2RGB
に現れる2つの文字
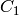 と
と
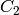 は,パターンの種類を表しています.
つまり,この2文字は,あるパターンの2行目の2,3番目の成分であり,例えば,上述の図で表されたパターンは,まさに “BG” タイプです.
は,パターンの種類を表しています.
つまり,この2文字は,あるパターンの2行目の2,3番目の成分であり,例えば,上述の図で表されたパターンは,まさに “BG” タイプです.
cv::distanceTransform¶
- void distanceTransform(const Mat& src, Mat& dst, Mat& labels, int distanceType, int maskSize)
入力画像中の非0ピクセルから,最も近い0ピクセルまでの距離を,全ての非0ピクセルに対して計算します.
パラメタ: - src – 8ビット,シングルチャンネル(2値)の入力画像
- dst – 求められた距離を値とする出力画像. src と同じサイズの,32ビット,浮動小数点型,シングルチャンネル画像
- distanceType – 距離の種類. CV_DIST_L1, CV_DIST_L2 あるいは CV_DIST_C
- mask_size – 距離変換マスクのサイズ.3,5 あるいは CV_DIST_MASK_PRECISE (後者のオプションは,1番目の関数形式でのみサポートされます). CV_DIST_L1 または CV_DIST_C の場合,距離の種類は強制的に 3 になります.なぜなら,この場合
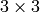 のマスクは
のマスクは 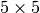 以上のマスクと同じ結果で計算速度が速いからです
以上のマスクと同じ結果で計算速度が速いからです - labels – オプション.出力されるラベルの2次元配列.離散ボロノイ図.このタイプは CV_32SC1 で, src と同じサイズになる.説明を参照してください
関数 distanceTransform は,2値画像の各ピクセルから,最も近い値0のピクセルまでの近似距離または正確な距離を求めます(値が0のピクセルからの距離は,もちろん0).
maskSize == CV_DIST_MASK_PRECISE かつ distanceType == CV_DIST_L2 の場合,この関数は Felzenszwalb04 で述べられているアルゴリズムを実行します.
その他の場合は,
Borgefors86
のアルゴリズムが利用されます.つまり,基本移動の組み合わせで0ピクセルに至るまでの最短距離を見つけます.
この基本移動とは,水平,垂直,斜め,桂馬飛び(これは
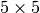 サイズのマスクを利用した場合のみ)移動です.
これらの基本移動距離の合計が全長距離となります.
距離関数は対称性をもつはずなので,水平および垂直移動のコスト(これを
a
で表します)は全て等しくなければいけません.同様に,斜め移動のコスト(これを
b
で表します)もすべて等しく,桂馬飛び移動のコスト(これを
c
で表します)もすべて等しくなくてはいけません.距離の種類が
CV_DIST_C
や
CV_DIST_L1
の場合,距離は正確に計算されますが,
CV_DIST_L2
(ユークリッド距離)の場合は,距離にいくらかの相対誤差(
サイズのマスクを利用した場合のみ)移動です.
これらの基本移動距離の合計が全長距離となります.
距離関数は対称性をもつはずなので,水平および垂直移動のコスト(これを
a
で表します)は全て等しくなければいけません.同様に,斜め移動のコスト(これを
b
で表します)もすべて等しく,桂馬飛び移動のコスト(これを
c
で表します)もすべて等しくなくてはいけません.距離の種類が
CV_DIST_C
や
CV_DIST_L1
の場合,距離は正確に計算されますが,
CV_DIST_L2
(ユークリッド距離)の場合は,距離にいくらかの相対誤差(
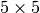 マスクを用いると精度が向上する)が含まれます.OpenCVでは,
a
,
b
および
c
の値として,元論文で述べられている値を利用しています:
マスクを用いると精度が向上する)が含まれます.OpenCVでは,
a
,
b
および
c
の値として,元論文で述べられている値を利用しています:
| CV_DIST_C | 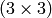 |
a = 1, b = 1 |
|---|---|---|
| CV_DIST_L1 | 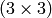 |
a = 1, b = 2 |
| CV_DIST_L2 | 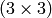 |
a=0.955, b=1.3693 |
| CV_DIST_L2 | 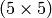 |
a=1, b=1.4, c=2.1969 |
通常は,高速化のために,粗い距離推定
CV_DIST_L1
では
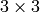 のマスクが利用され,
より正確な距離推定
CV_DIST_L2
では
のマスクが利用され,
より正確な距離推定
CV_DIST_L2
では
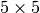 のマスクが利用されます.
のマスクが利用されます.
粗い推定と正確な推定のどちらのアルゴリズムも,ピクセル数に対して線形であることに注意してください.
2番目の関数形式は,各ピクセル
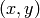 に対する最小距離だけでなく,0ピクセルで構成された連結成分のうち最も近いものを特定します.
そして,その連結成分のインデックスが
に対する最小距離だけでなく,0ピクセルで構成された連結成分のうち最も近いものを特定します.
そして,その連結成分のインデックスが
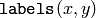 に格納されます.検出された0ピクセルの連結成分は,この関数によってマークされます.
に格納されます.検出された0ピクセルの連結成分は,この関数によってマークされます.
このモードでも,計算量は線形です.つまり,この関数を使って,2値画像に対するボロノイ図を非常に高速に計算できるということです.現在のところ,この2番目の形式では,近似距離変換アルゴリズムのみが利用可能です.
cv::floodFill¶
- int floodFill(Mat& image, Point seed, Scalar newVal, Rect* rect=0, Scalar loDiff=Scalar(), Scalar upDiff=Scalar(), int flags=4)¶
- int floodFill(Mat& image, Mat& mask, Point seed, Scalar newVal, Rect* rect=0, Scalar loDiff=Scalar(), Scalar upDiff=Scalar(), int flags=4)
連結成分を指定した色で塗りつぶします.
パラメタ: - image – 1または3チャンネル,8ビットまたは浮動小数点型の入出力画像.フラグ CV_FLOODFILL_MASK_ONLY が指定されている場合を除き,この関数によって書き換えられます(2番目の関数形式の場合.以下を参照してください)
- mask – (2番目の形式の場合のみ)オプション.8ビット,シングルチャンネルのマスク画像.入力画像よりも,幅高さ共に2ピクセルずつ大きくなります.関数はこのマスク画像を利用し更新を行うので,ユーザは mask の中身をきちんと初期化しておかなければいけません.この塗りつぶしは,マスク画像中の0ではないピクセルを飛び越えることはできません.例えば,エッジ検出の出力画像は,塗りつぶしをエッジ部分で堰き止めるためのマスク画像として利用できます.また,塗りつぶされる領域同士が重ならないよう,複数回の関数呼び出しで同じマスク画像を利用することができます. 注意 :マスク画像は塗りつぶされる画像よりも大きいので, image 中のピクセル
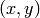 に対応する mask 中のピクセルは
に対応する mask 中のピクセルは 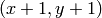 となります
となります - seed – 連結成分の開始点
- newVal – 領域の塗りつぶしに使う新しいピクセル値
- loDiff – 現在の対象ピクセルと,その連結成分に属する隣接ピクセルの1つとの間での,あるいは連結成分に追加されるシードピクセルとの間での,輝度値/色の差の許容下限値
- upDiff – 現在の対象ピクセルと,その連結成分に属する隣接ピクセルの1つとの間での, あるいは連結成分に追加されるシードピクセルとの間での,輝度値/色の差の許容上限値
- rect – オプション.この関数によって塗りつぶされた領域の最小の包含矩形がセットされる出力パラメータ
- flags –
処理フラグ.下位ビットには,連結性を表す値である 4(デフォルト)あるいは 8 が含まれ,これらの値は関数内部で利用されます.この連結性は,どの隣接ピクセルを処理するべきかを定義します.上位ビットは,0 あるいは以下のフラグの組み合わせ:
- FLOODFILL_FIXED_RANGE これが指定されている場合,現在のピクセルとシードピクセルとの間の差だけが考慮されます.指定されていなければ,隣接ピクセル同士の差が考慮されます(つまり,差の許容範囲が変動します)
- FLOODFILL_MASK_ONLY (2番目の関数形式の場合のみ)これが指定されている場合,この関数は画像を塗りつぶさずに(引数 new_val は無視されます),マスクを塗りつぶします
関数
floodFill
は,指定された色で連結成分を塗りつぶします.塗りつぶしは,シードピクセルから開始されます.連結しているかどうかは,隣接ピクセル値同士の色/輝度値の距離によって決まります.
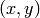 のピクセルが塗りつぶされる領域に属していると見なされるのは,以下の場合です:
のピクセルが塗りつぶされる領域に属していると見なされるのは,以下の場合です:
グレースケール画像,変動範囲
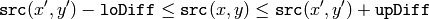
グレースケール画像,固定範囲
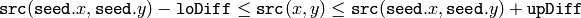
カラー画像,変動範囲
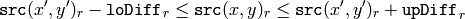
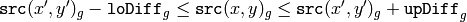
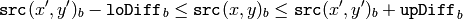
カラー画像,固定範囲
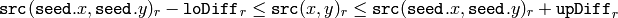
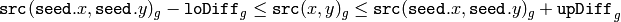
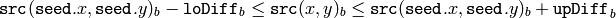
ここで,
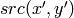 は,ある隣接ピクセルのピクセル値を表します.つまり,対象ピクセルの色/輝度値が,次の値に十分近い場合に連結成分に追加されます:
は,ある隣接ピクセルのピクセル値を表します.つまり,対象ピクセルの色/輝度値が,次の値に十分近い場合に連結成分に追加されます:
- 変動範囲の場合:既に連結成分に属する隣接ピクセルの色/輝度値
- 固定範囲の場合:シードピクセルの色/輝度値.
これらの関数を利用すると,連結成分を指定色で塗りつぶしてマークする,マスクを作成して輪郭を抽出する,あるいは領域を別の画像にコピーする,といったことが可能になります.この関数の様々なモードは,サンプル floodfill.c でデモされます.
参考: findContours()
cv::inpaint¶
- void inpaint(const Mat& src, const Mat& inpaintMask, Mat& dst, double inpaintRadius, int flags)¶
選択領域内の画像を修復します.
パラメタ: - src – 入力画像.8ビット,1あるいは3チャンネル
- inpaintMask – 8ビット,1チャンネルの修復マスク.非0のピクセルが,修復が必要な領域を表します
- dst – src と同じサイズ,同じタイプの出力画像
- inpaintRadius – 修復される点(これはアルゴリズムにより判断されます)周りの円形の近傍領域の半径
- flags –
修復手法.以下のいずれか:
- INPAINT_NS ナビエ・ストークス(Navier-Stokes)ベースの手法
- INPAINT_TELEA Alexandru Telea による手法 Telea04
関数 inpaint は,選択された画像領域を,その領域境界付近のピクセルを利用して再構成します.この関数は,スキャンされた写真からごみや傷を除去したり,静止画や動画から不要な物体を削除したりするために利用されます.詳しくは http://en.wikipedia.org/wiki/Inpainting を参照してください.
cv::integral¶
- void integral(const Mat& image, Mat& sum, Mat& sqsum, Mat& tilted, int sdepth=-1)
インテグラルイメージを求めます.
パラメタ: - image – 入力画像,
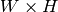 の8ビット,あるいは浮動小数点型(32f または 64f)
の8ビット,あるいは浮動小数点型(32f または 64f) - sum – インテグラルイメージ,
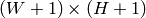 の32ビット整数,あるいは倍精度浮動小数点型(64f)
の32ビット整数,あるいは倍精度浮動小数点型(64f) - sqsum – 各ピクセル値を2乗した画像に対するインテグラルイメージ,
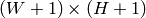 の倍精度浮動小数点型(64f)
の倍精度浮動小数点型(64f) - tilted – 45度回転した画像に対するインテグラルイメージ,
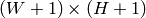 で,データの型は sum と同じ
で,データの型は sum と同じ - sdepth – インテグラルイメージ,傾いたインテグラルイメージのビット深度. CV_32S , CV_32F あるいは CV_64F
- image – 入力画像,
関数 integral は,入力画像に対する1つあるいは複数のインテグラルイメージを次のように求めます:
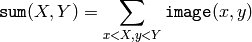
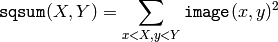
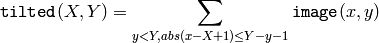
このようなインテグラルイメージを用いると,画像中の任意の矩形領域(あるいは45度回転した矩形領域)の画素値の総和,平均,標準偏差を定数時間で計算できます.例えば:
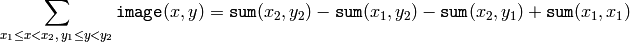
これを用いて,例えば,窓サイズ可変な平滑化や相関演算を高速に計算することが可能です.マルチチャンネル画像の場合は,各チャンネルでの総和が個別に累積されます.
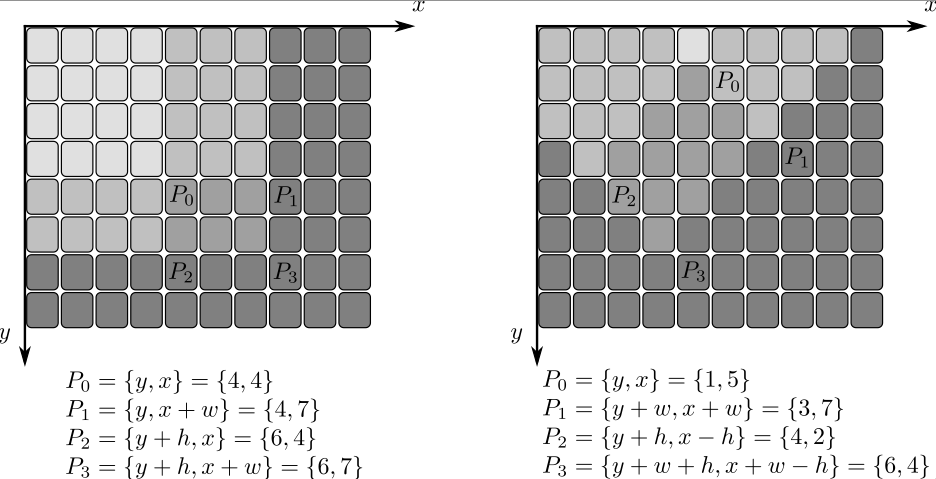
実際の例として,次の図では,直立した矩形 Rect(3,3,3,2) のインテグラルイメージと傾いた矩形 Rect(5,1,2,3) のインテグラルイメージの計算について示します.インテグラルイメージ sum と tilted 中の関連ピクセルと一緒に,その元画像 image における選択ピクセルが表示されています.
begin{center}
end{center}
cv::threshold¶
- double threshold(const Mat& src, Mat& dst, double thresh, double maxVal, int thresholdType)¶
配列の要素に対して,ある定数での閾値処理を行います.
パラメタ: - src – 入力配列(シングルチャンネル,8ビット,あるいは32ビット浮動小数点型)
- dst – src と同じサイズ,同じタイプの出力配列
- thresh – 閾値
- maxVal – 閾値処理の種類が THRESH_BINARY や THRESH_BINARY_INV の場合に利用される,最大値の値
- thresholdType – 閾値処理の種類(以下の説明を参照してください)
この関数は,シングルチャンネルの配列に対して,ある定数での閾値処理を行います.これは,グレースケールからの2値画像生成(関数 compare も,この目的に利用できます)やノイズ除去(つまり,小さすぎたり大きすぎたりする値をはじく処理)などに利用される場合が多いです.この関数がサポートする閾値処理にはいくつかの種類があり,それは引数 thresholdType によって決定されます:
THRESH_BINARY
THRESH_BINARY_INV
THRESH_TRUNC
THRESH_TOZERO
THRESH_TOZERO_INV
また,特殊な値 THRESH_OTSU を,上述のものと組み合わせて使うこともできます.この場合,関数は大津のアルゴリズムを用いて最適な閾値を決定し,それを引数 thresh で指定された値の代わりに利用します.この関数は,計算された閾値を返します.また現在のところ,大津の手法は 8ビット画像に対してのみ実装されています.
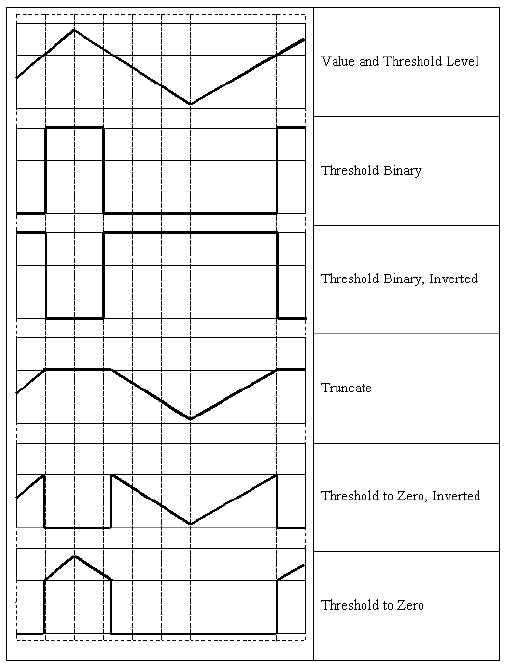
参考: adaptiveThreshold() , findContours() , compare() , min() , max()
cv::watershed¶
- void watershed(const Mat& image, Mat& markers)¶
watershedアルゴリズムを用いて,マーカベースの画像セグメンテーションを行います.
パラメタ: - image – 8ビット,3チャンネルの入力画像
- markers – 32ビット,シングルチャンネルの,マーカ入出力画像(マップ). image と同じサイズ
この関数は,参考文献
Meyer92
で述べられた,ノンパラメトリックなマーカベースのセグメンテーションアルゴリズムである Watershed のバリエーションの1つを実装したものです.
画像をこの関数に渡す前に,ユーザは画像をどのような領域に分割したいかを大まかに決めて,それを正(
 )のインデックスで
markers
内に書き込んでおく必要があります.つまり,その場合の各領域は,1,2,3と
いったピクセル値をもつ1つあるいは複数の連結成分で表現されます(このようなマーカは,
findContours
や
drawContours
を用いて2値マスクから抽出できます.
watershed.cpp
を参照してください).
そして,このような連結成分は,画像領域分割のための「シード」となります.また,
markers
内のその他のピクセルは,どの領域に属するかが未知であり,それはこのアルゴリズムによって定義されますが,まずは最初に 0 にセットされなければいけません.
この関数の出力である markers 内の各ピクセルには,「シード」成分の値の1つがセットされます.また,領域の境界に位置するピクセルの場合は -1 がセットされます.
)のインデックスで
markers
内に書き込んでおく必要があります.つまり,その場合の各領域は,1,2,3と
いったピクセル値をもつ1つあるいは複数の連結成分で表現されます(このようなマーカは,
findContours
や
drawContours
を用いて2値マスクから抽出できます.
watershed.cpp
を参照してください).
そして,このような連結成分は,画像領域分割のための「シード」となります.また,
markers
内のその他のピクセルは,どの領域に属するかが未知であり,それはこのアルゴリズムによって定義されますが,まずは最初に 0 にセットされなければいけません.
この関数の出力である markers 内の各ピクセルには,「シード」成分の値の1つがセットされます.また,領域の境界に位置するピクセルの場合は -1 がセットされます.
2つの隣接した連結成分が,必ずしも watershed 境界(-1 の値をもつピクセル)によって分割されるわけではないことに注意してください.例えば,初期 marker に接線成分が存在する場合などがこれにあたります.この関数の実際のデモと使用例については,OpenCVサンプルディレクトリにある watershed.cpp デモを参照してください.
参考: findContours()
ヘルプとフィードバック
お探しの情報が見つかりませんか?- FAQ (英語)を試してください.
- ユーザグループ/メーリングリスト (英語)で質問してみてください.
- このドキュメントに誤りなどを見つけたらbug report まで報告してください.また,日本語訳に関する誤りや指摘はopencv.jpまでお願い します.