構造解析と形状ディスクリプタ¶
cv::moments¶
ここで Moments クラス は次のように定義されます:
class Moments
{
public:
Moments();
Moments(double m00, double m10, double m01, double m20, double m11,
double m02, double m30, double m21, double m12, double m03 );
Moments( const CvMoments& moments );
operator CvMoments() const;
// 空間モーメント
double m00, m10, m01, m20, m11, m02, m30, m21, m12, m03;
// 中心モーメント
double mu20, mu11, mu02, mu30, mu21, mu12, mu03;
// 正規化された中心モーメント
double nu20, nu11, nu02, nu30, nu21, nu12, nu03;
};
param array: ラスタ画像(シングルチャンネル,8ビットまたは浮動小数点型の2次元配列)あるいは,2次元点( Point または Point2f )の配列( または
)
param binaryImage: (画像の場合のみ)これが真の場合,すべての非0ピクセルが1として扱われます
関数
moments
は,ベクタ形状またはラスタライズされた形状の,3次までのモーメントを求めます.ラスタ画像の場合,空間モーメント
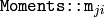 は次のように求められます:
は次のように求められます:
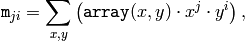
また,中心モーメント
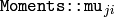 は,次のように求められます:
は,次のように求められます:
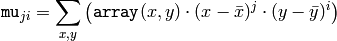
ここで
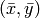 は重心を表します:
は重心を表します:
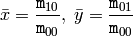
また,正規化された中心モーメント
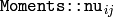 は次のように求められます:
は次のように求められます:
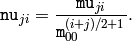
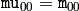 ,
,
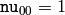
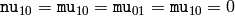 となるので,これらの値は保存されないことに注意してください.
となるので,これらの値は保存されないことに注意してください.
輪郭のモーメントも同様に定義されますが,これはグリーンの定理を用いて求められます( http://en.wikipedia.org/wiki/Green_theorem を参照してください).したがって,ラスタライズの分解能の制限により,輪郭に対して計算されたモーメントは,ラスタライズされた同じ輪郭に対して計算されたものとは多少異なります.
参考: contourArea() , arcLength()
cv::HuMoments¶
- void HuMoments(const Moments& moments, double h[7])¶
7つの Hu モーメント不変量を求めます.
パラメタ: - moments – moments() で求められた入力モーメント
- h – 出力される Hu 不変量
関数 HuMoments は,次のように定義される7つの Hu 不変量( http://en.wikipedia.org/wiki/Image_moment を参照)を求めます.
![\begin{array}{l} h[0]= \eta _{20}+ \eta _{02} \\ h[1]=( \eta _{20}- \eta _{02})^{2}+4 \eta _{11}^{2} \\ h[2]=( \eta _{30}-3 \eta _{12})^{2}+ (3 \eta _{21}- \eta _{03})^{2} \\ h[3]=( \eta _{30}+ \eta _{12})^{2}+ ( \eta _{21}+ \eta _{03})^{2} \\ h[4]=( \eta _{30}-3 \eta _{12})( \eta _{30}+ \eta _{12})[( \eta _{30}+ \eta _{12})^{2}-3( \eta _{21}+ \eta _{03})^{2}]+(3 \eta _{21}- \eta _{03})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}] \\ h[5]=( \eta _{20}- \eta _{02})[( \eta _{30}+ \eta _{12})^{2}- ( \eta _{21}+ \eta _{03})^{2}]+4 \eta _{11}( \eta _{30}+ \eta _{12})( \eta _{21}+ \eta _{03}) \\ h[6]=(3 \eta _{21}- \eta _{03})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}]-( \eta _{30}-3 \eta _{12})( \eta _{21}+ \eta _{03})[3( \eta _{30}+ \eta _{12})^{2}-( \eta _{21}+ \eta _{03})^{2}] \\ \end{array}](_images/math/8abf2554aad5cce3dd3291abe515b3a8dcc3a1bd.png)
ここで
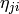 は
は
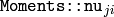 の省略形です.
の省略形です.
反転によって符号が逆転してしまう7番目のHuモーメントを除いて,これらの値は,画像のスケール変化,回転,および反転に対して不変であることが分かっています.この不変量は,もちろん画像解像度が有限であるという仮定の元に成り立っています.ラスタ画像の場合は,元画像に対する Hu 不変量と変形した画像に対するものとは多少異なります.
参考: matchShapes()
cv::findContours¶
- void findContours(const Mat& image, vector<vector<Point> >& contours, vector<Vec4i>& hierarchy, int mode, int method, Point offset=Point())¶
- void findContours(const Mat& image, vector<vector<Point> >& contours, int mode, int method, Point offset=Point())
2値画像中の輪郭を検出します.
パラメタ: - image – 入力画像,8ビット,シングルチャンネル.0以外のピクセルは 1として,0のピクセルは0のまま扱われます.つまり,入力画像は 2値画像 として扱われます.グレースケールやカラー画像から2値画像を得るには, compare() , inRange() , threshold() , adaptiveThreshold() , Canny() などの関数を利用します.また,この関数は,輪郭抽出処理中に入力画像 image の中身を書き換えます
- contours – 検出された輪郭.各輪郭は,点のベクトルとして格納されます
- hiararchy – オプション.画像のトポロジーに関する情報を含む出力ベクトル.これは,輪郭数と同じ数の要素を持ちます.各輪郭 contours[i] に対して,要素 hierarchy[i][0] , hiearchy[i][1] , hiearchy[i][2] , hiearchy[i][3] にはそれぞれ,同じ階層レベルに存在する前後の輪郭,最初の子輪郭,および親輪郭の contours インデックス(0 基準)がセットされます.また,輪郭 i において,前後,親,子の輪郭が存在しない場合,それに対応する hierarchy[i] の要素は,負の値になります
- mode –
輪郭抽出モード
- CV_RETR_EXTERNAL 最も外側の輪郭のみを抽出します.すべての輪郭に対して hierarchy[i][2]=hierarchy[i][3]=-1 がセットされます
- CV_RETR_LIST すべての輪郭を抽出しますが,一切の階層構造を保持しません
- CV_RETR_CCOMP 全ての輪郭を抽出し,それらを2階層構造として保存します:上のレベルには,連結成分の外側の境界線が,下のレベルには,連結成分の内側に存在する穴の境界線が属します.ある連結成分の穴の内側に別の輪郭が存在する場合,その穴は上のレベルに属します
- CV_RETR_TREE 全ての輪郭を抽出し,入れ子構造になった輪郭を完全に表現する階層構造を構成します.この完全な階層構造は,OpenCVの contours.c デモで見ることができます
- method –
輪郭の近似手法:
- CV_CHAIN_APPROX_NONE すべての輪郭点を完全に格納します.つまり,この手法により格納された任意の隣り合う2点は,互いに8近傍に存在します
- CV_CHAIN_APPROX_SIMPLE 水平・垂直・斜めの線分を圧縮し,それらの端点のみを残します.例えば,まっすぐな矩形の輪郭線は,4つの点にエンコードされます
- CV_CHAIN_APPROX_TC89_L1,CV_CHAIN_APPROX_TC89_KCOS Teh-Chinチェーン近似アルゴリズムの1つを適用します. TehChin89 を参照してください
- offset – オプションのオフセット.各輪郭点はこの値の分だけシフトします.これは,ROIの中で抽出された輪郭を,画像全体に対して位置づけて解析する場合に役立ちます
関数 findContours は, Suzuki85 のアルゴリズムを利用して,2値画像から輪郭を抽出します.この輪郭は,形状の解析や物体検出,物体認識のための便利な道具となります.OpenCV のサンプルディレクトリにある squares.c を参照してください.
注意: 元の image は,この関数によって書き換えられます.
cv::drawContours¶
- void drawContours(Mat& image, const vector<vector<Point> >& contours, int contourIdx, const Scalar& color, int thickness=1, int lineType=8, const vector<Vec4i>& hierarchy=vector<Vec4i>(), int maxLevel=INT_MAX, Point offset=Point())¶
輪郭線,または内側が塗りつぶされた輪郭を描きます.
パラメタ: - image – 出力画像
- contours – 入力される全輪郭.各輪郭は,点のベクトルとして格納されています
- contourIdx – 描かれる輪郭を示します.これが負値の場合,すべての輪郭が描画されます
- color – 輪郭の色
- thickness – 輪郭線の太さ.これが負値の場合(例えば thickness=CV_FILLED ),輪郭の内側が塗りつぶされます
- lineType – 線の連結性. line() の説明を参照してください
- hierarchy – 階層に関するオプションの情報.これは,特定の輪郭だけを描画したい場合にのみ必要になります
- maxLevel – 描画される輪郭の最大レベル.0ならば,指定された輪郭のみが描画されます.1ならば,指定された輪郭と,それに入れ子になったすべての輪郭が描画されます.2ならば,指定された輪郭と,それに入れ子になったすべての輪郭,さらにそれに入れ子になったすべての輪郭が描画されます.このパラメータは, hierarchy が有効な場合のみ考慮されます
- offset – 輪郭をシフトするオプションパラメータ.指定された
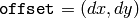 だけ,すべての描画輪郭がシフトされます
だけ,すべての描画輪郭がシフトされます
関数
drawContours
は,
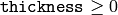 ならば画像に輪郭線を描き,
ならば画像に輪郭線を描き,
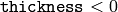 ならば輪郭で囲まれた領域を塗りつぶします.ここでは,2値画像から連結性分を抽出し,それらをラベリングする例を示します:
ならば輪郭で囲まれた領域を塗りつぶします.ここでは,2値画像から連結性分を抽出し,それらをラベリングする例を示します:
#include "cv.h"
#include "highgui.h"
using namespace cv;
int main( int argc, char** argv )
{
Mat src;
// コマンドライン引数の 1 番目に 2 値画像(白黒)
// のファイル名を与えてください.
if( argc != 2 || !(src=imread(argv[1], 0)).data)
return -1;
Mat dst = Mat::zeros(src.rows, src.cols, CV_8UC3);
src = src > 1;
namedWindow( "Source", 1 );
imshow( "Source", src );
vector<vector<Point> > contours;
vector<Vec4i> hierarchy;
findContours( src, contours, hierarchy,
CV_RETR_CCOMP, CV_CHAIN_APPROX_SIMPLE );
// トップレベルにあるすべての輪郭を横断し,
// 各連結成分をランダムな色で描きます.
int idx = 0;
for( ; idx >= 0; idx = hiearchy[idx][0] )
{
Scalar color( rand()&255, rand()&255, rand()&255 );
drawContours( dst, contours, idx, color, CV_FILLED, 8, hiearchy );
}
namedWindow( "Components", 1 );
imshow( "Components", dst );
waitKey(0);
}
cv::approxPolyDP¶
- void approxPolyDP(const Mat& curve, vector<Point2f>& approxCurve, double epsilon, bool closed)
折れ線カーブを指定された精度で近似します.
パラメタ: - curve – 近似されるポリゴン,またはカーブ.
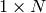 または
または 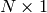 の行列で,その型は CV_32SC2 または CV_32FC2 です.また,コンストラクタ Mat(const vector<T>&) を呼び出すことで, vector<Point> または vector<Point2f> をこのような行列に変換することもできます
の行列で,その型は CV_32SC2 または CV_32FC2 です.また,コンストラクタ Mat(const vector<T>&) を呼び出すことで, vector<Point> または vector<Point2f> をこのような行列に変換することもできます - approxCurve – 近似結果.入力されたカーブの型と同じ型です
- epsilon – 近似精度を指定します.これは,元のカーブと近似カーブの最大距離です
- closed – これが真の場合,近似された曲線は閉じたものになり(つまり,最初と最後の頂点が接続されます),そうでない場合は,開いた曲線になります
- curve – 近似されるポリゴン,またはカーブ.
関数 approxPolyDP は,折れ線カーブまたはポリゴンを,互いの距離が指定された精度以下になるように,より少ない頂点数のカーブやポリゴンで近似します.ここでは Douglas-Peucker アルゴリズム http://en.wikipedia.org/wiki/Ramer-Douglas-Peucker_algorithm が利用されます.
cv::arcLength¶
- double arcLength(const Mat& curve, bool closed)¶
輪郭線の周囲長,あるいは曲線の長さを求めます.
パラメタ: - curve – 入力される2次元点のベクトル. CV_32SC2 または CV_32FC2 の行列,あるいは,コンストラクタ Mat(const vector<T>&) により行列に変換される vector<Point> または vector<Point2f> のベクトルで表現されます
- closed – カーブが開いているか閉じているかを示します
この関数は,輪郭線の周囲長,あるいは曲線の長さを求めます.
cv::boundingRect¶
- Rect boundingRect(const Mat& points)¶
点群を包含する傾いていない最小の矩形を求めます.
Parameter: points – 入力される2次元点の集合. CV_32SC2 または CV_32FC2 の行列,あるいは,コンストラクタ Mat(const vector<T>&) により行列に変換される vector<Point> または vector<Point2f> のベクトルで表現されます
この関数は,指定された点群を包含する傾いていない最小の矩形を求め,それを返します.
cv::estimateRigidTransform¶
- Mat estimateRigidTransform(const Mat& srcpt, const Mat& dstpt, bool fullAffine)¶
2次元点集合間の最適なアフィン変換を求めます.
パラメタ: - srcpt – 1番目の2次元点集合
- dstpt – srcpt と同じサイズ,同じ型の2番目の2次元点集合
- fullAffine – これが真の場合,この関数は,制約条件を追加することなく最適なアフィン変換を求めます(つまり,6自由度).そうでない場合,並進,回転および等方性スケーリングの組み合わせ(つまり,5自由度)から変換を求めます
この関数は,
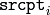 から
から
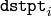 への変換を最も良く近似する,最適なアフィン変換
への変換を最も良く近似する,最適なアフィン変換
![[A|b]](_images/math/5811dc4a2ff4e426ab272d1d4da6988db5790e51.png) (
(
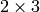 の浮動小数点型行列)を求めます:
の浮動小数点型行列)を求めます:
![[A^*|b^*] = arg \min _{[A|b]} \sum _i \| \texttt{dstpt} _i - A { \texttt{srcpt} _i}^T - b \| ^2](_images/math/4cb9f8958a90e9902498766c05c0f252459343d1.png)
ここで
fullAffine=true
の場合は
![[A|b]](_images/math/5811dc4a2ff4e426ab272d1d4da6988db5790e51.png) は任意の行列になりますが,
fullAffine=false
の場合は
は任意の行列になりますが,
fullAffine=false
の場合は
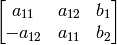
という形式になります.
参考: getAffineTransform() , getPerspectiveTransform() , findHomography()
cv::estimateAffine3D¶
- int estimateAffine3D(const Mat& srcpt, const Mat& dstpt, Mat& out, vector<uchar>& outliers, double ransacThreshold = 3.0, double confidence = 0.99)¶
Computes optimal affine transformation between two 3D point sets
パラメタ: - srcpt – 1番目の3次元点集合
- dstpt – 2番目の3次元点集合
- out – 出力される,
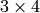 の3次元アフィン変換行列
の3次元アフィン変換行列 - outliers – 外れ値である点を示す出力ベクトル
- ransacThreshold – RANSACアルゴリズムにおいて外れ値ではないと見なされる,逆投影誤差の最大値
- confidence – 0 から 1 の値で表現される,推定された行列の信頼レベル
この関数は,RANSACアルゴリズムを用いて,3次元点集合間の最適な3次元アフィン変換を求めます.
cv::contourArea¶
- double contourArea(const Mat& contour)¶
輪郭が囲む領域の面積を求めます.
Parameter: contour – 輪郭の頂点. CV_32SC2 または CV_32FC2 の行列,あるいは,コンストラクタ Mat(const vector<T>&) により行列に変換される vector<Point> または vector<Point2f> のベクトルで表現されます
この関数は,輪郭の囲む領域の面積を求めます. moments() と同様にグリーンの定理を利用して面積を求めるので, drawContours() や fillPoly() を用いて輪郭を描画しても,その面積と非0ピクセルの数は異なります.
ここでは,短い例を示します:
vector<Point> contour;
contour.push_back(Point2f(0, 0));
contour.push_back(Point2f(10, 0));
contour.push_back(Point2f(10, 10));
contour.push_back(Point2f(5, 4));
double area0 = contourArea(contour);
vector<Point> approx;
approxPolyDP(contour, approx, 5, true);
double area1 = contourArea(approx);
cout << "area0 =" << area0 << endl <<
"area1 =" << area1 << endl <<
"approx poly vertices" << approx.size() << endl;
cv::convexHull¶
- void convexHull(const Mat& points, vector<Point>& hull, bool clockwise=false)
- void convexHull(const Mat& points, vector<Point2f>& hull, bool clockwise=false)
点集合に対する凸包を求めます.
パラメタ: - points – 入力される2次元点のベクトル. CV_32SC2 または CV_32FC2 の行列で表現されます.あるいは,コンストラクタ Mat(const vector<T>&) により行列に変換される vector<Point> または vector<Point2f> のベクトルで表現されます
- hull – 出力される凸包.凸包を構成する点のベクトル,あるいは,凸包を構成する点の元の配列におけるインデックス(0基準)のベクトルです(凸包の点集合は元の点集合の部分集合となるので)
- clockwise – これが真の場合,出力される凸包は時計回りになり,そう でなければ反時計回りになります.ここで,スクリーンの座標系は左上原点,x軸は右向き,y軸は下向きであると仮定しています
この関数は, Sklansky のアルゴリズム
Sklansky82
を利用して2次元点集合の凸包を求めます.計算量は
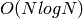 または
または
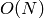 であり(
であり(
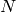 は入力点数を表す),これは初期ソートの実装に依存します(現在は
は入力点数を表す),これは初期ソートの実装に依存します(現在は
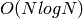 ).この関数の各形式の利用方法を実演する OpenCV のサンプル
convexhull.c
を参照してください.
).この関数の各形式の利用方法を実演する OpenCV のサンプル
convexhull.c
を参照してください.
cv::fitEllipse¶
- RotatedRect fitEllipse(const Mat& points)¶
2次元の点集合に楕円をフィッティングします.
Parameter: points – 入力される2次元点の集合. CV_32SC2 または CV_32FC2 の行列,あるいは,コンストラクタ Mat(const vector<T>&) により行列に変換される vector<Point> または vector<Point2f> のベクトルで表現されます
関数 fitEllipse は,2次元点の集合に最もフィットする(二乗誤差が最小になる)楕円を求めます.その楕円に外接する,回転を考慮した矩形が返されます.
cv::fitLine¶
- void fitLine(const Mat& points, Vec6f& line, int distType, double param, double reps, double aeps)
2次元あるいは3次元の点集合に直線をフィッティングします.
パラメタ: - points – 入力される2次元点の集合. CV_32SC2 または CV_32FC2 の行列,あるいは,コンストラクタ Mat(const vector<T>&) により行列に変換される vector<Point> または vector<Point2f> のベクトルで表現されます
- line – 出力される直線パラメータ.2次元フィッティングの場合,これは4つの浮動小数点数 (vx, vy, x0, y0) のベクトルとなります.ここで, (vx, vy) は正規化された直線方向ベクトル, (x0, y0) は直線上の点を表します.3次元フィッティングの場合,これは6つの浮動小数点数 (vx, vy, vz, x0, y0, z0) のベクトルとなります.ここで, (vx, vy, vz) は正規化された直線方向ベクトル, (x0, y0, z0) は直線上の点を表します
- distType – M-推定で利用される距離(説明を参照)
- param – ある種の距離で用いられる数値パラメータ ( C ).0の場合は最適な値が選択されます
- reps, aeps – それぞれ半径(座標原点と直線との距離)および角度に対する精度を表します.デフォルト値の0.01は,両方に対して適切な値です
関数
fitLine
は,
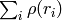 を最小化することで,2次元あるいは3次元の点集合に直線をフィッティングします.ここで,
を最小化することで,2次元あるいは3次元の点集合に直線をフィッティングします.ここで,
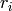 は
は
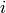 番目の点と直線の距離,
番目の点と直線の距離,
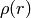 は距離関数(以下の内の1つ)を表します:
は距離関数(以下の内の1つ)を表します:
distType=CV_DIST_L2
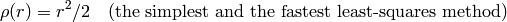
distType=CV_DIST_L1
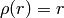
distType=CV_DIST_L12

distType=CV_DIST_FAIR
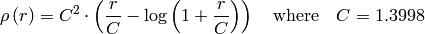
distType=CV_DIST_WELSCH
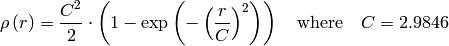
distType=CV_DIST_HUBER
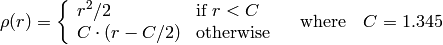
このアルゴリズムは,M-推定(
http://en.wikipedia.org/wiki/M-estimator
)に基づいており,重み付き最小二乗アルゴリズムを用いて反復フィッティングを行います.各試行の度に,
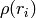 に反比例するように重み
に反比例するように重み
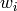 が調整されます.
が調整されます.
cv::isContourConvex¶
- bool isContourConvex(const Mat& contour)¶
輪郭形状が凸であるかを調べます.
Parameter: contour – 調べられる輪郭. CV_32SC2 または CV_32FC2 の行列,あるいは,コンストラクタ Mat(const vector<T>&) により行列に変換される vector<Point> または vector<Point2f> のベクトルで表現されます
関数 isContourConvex は,入力された輪郭が凸であるかどうかを調べます.輪郭は,自己交差しないような単純なものでなければならず,そうでない場合の出力は未定義です.
cv::minAreaRect¶
- RotatedRect minAreaRect(const Mat& points)¶
与えられた2次元点集合を囲む,(回転を考慮した)最小の矩形を求めます.
Parameter: points – 入力される2次元点の集合. CV_32SC2 または CV_32FC2 の行列,あるいは,コンストラクタ Mat(const vector<T>&) により行列に変換される vector<Point> または vector<Point2f> のベクトルで表現されます
この関数は,指定された点の集合を囲む(回転してるかもしれない)最小の矩形領域を求めます.OpenCVのサンプル minarea.c を参照してください.
cv::minEnclosingCircle¶
- void minEnclosingCircle(const Mat& points, Point2f& center, float& radius)¶
与えられた2次元点集合を囲む最小の円を求めます.
パラメタ: - points – 入力される2次元点の集合. CV_32SC2 または CV_32FC2 の行列,あるいは,コンストラクタ Mat(const vector<T>&) により行列に変換される vector<Point> または vector<Point2f> のベクトルで表現されます
- center – 出力される円の中心
- radius – 出力される円の半径
この関数は,反復アルゴリズムを用いて,与えられた2次元点集合を囲む最小の円を求めます.OpenCVのサンプル minarea.c を参照してください.
cv::matchShapes¶
- double matchShapes(const Mat& object1, const Mat& object2, int method, double parameter=0)¶
2つの形状を比較します.
パラメタ: - object1 – 1番目の輪郭またはグレースケール画像
- object2 – 2番目の輪郭またはグレースケール画像
- method –
比較手法:
CV_CONTOUR_MATCH_I1 , CV_CONTOURS_MATCH_I2
または
CV_CONTOURS_MATCH_I3 (see the discussion below)
- parameter – 比較手法毎のパラメータ(現在は利用されていません)
関数
matchShapes
は,2つの形状を比較します.実装されている3種類の手法は,以下に示すように,いずれもHuモーメント(
HuMoments()
の説明を参照してください)を利用します(
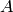 は
object1
,
は
object1
,
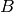 は
object2
を表しています):
は
object2
を表しています):
method=CV_CONTOUR_MATCH_I1
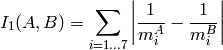
method=CV_CONTOUR_MATCH_I2
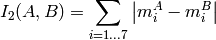
method=CV_CONTOUR_MATCH_I3
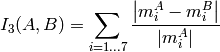
ここで
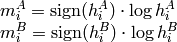
です.
また,
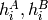 は,
は,
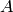 と
と
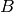 それぞれのHuモーメントを表します.
それぞれのHuモーメントを表します.
cv::pointPolygonTest¶
- double pointPolygonTest(const Mat& contour, Point2f pt, bool measureDist)¶
点と輪郭の関係を調べます.
パラメタ: - contour – 入力輪郭
- pt – 輪郭に対して調べられる点
- measureDist – これが真の場合,関数は与えられた点から最も近い輪郭辺までの符号付き距離を求めます.そうでない場合,点が輪郭の内側にあるか外側にあるかだけが調べられます
この関数は, 点が輪郭の内側にある か,外側にあるか,輪郭上に乗っている(あるいは,頂点と一致している)か を判別します.そして,それに応じて,正値(内側),負置(外側),0(辺上)を返します.
measureDist=false の場合は,戻り値はそれぞれ +1, -1, 0 になります. そうでない場合は,点と最も近い輪郭辺までの符号付き距離が戻り値となります.
ここでは,画像の各ピクセルと輪郭との関係を調べたときの出力を示します.

ヘルプとフィードバック
お探しの情報が見つかりませんか?- FAQ (英語)を試してください.
- ユーザグループ/メーリングリスト (英語)で質問してみてください.
- このドキュメントに誤りなどを見つけたらbug report まで報告してください.また,日本語訳に関する誤りや指摘はopencv.jpまでお願い します.
