モーション解析と物体追跡¶

cv::accumulate¶

void accumulate(const Mat& src, Mat& dst, const Mat& mask=Mat())¶

画像を累算器に加算します．

パラメタ:	src – 1- または 3-チャンネル，8ビットまたは 32ビット浮動小数点型の入力画像 dst – 入力画像と同じチャンネル数，32ビットまたは 64ビット浮動小数点型の累算器画像 mask – オプションである処理マスク

この関数は， src またはその一部の要素を， dst に加えます：

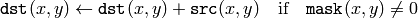
$\texttt{dst} (x,y) \leftarrow \texttt{dst} (x,y) + \texttt{src} (x,y) \quad \text{if} \quad \texttt{mask} (x,y) \ne 0$

この関数は，マルチチャンネル画像をサポートしており，各チャンネルは個別に処理されます．

関数 accumulate* は，例えば，前景と背景を上手く分離するために，固定カメラで撮影されたシーンの背景統計量を収集する際に利用されます．

参考： accumulateSquare() , accumulateProduct() , accumulateWeighted()

cv::accumulateSquare¶

void accumulateSquare(const Mat& src, Mat& dst, const Mat& mask=Mat())¶

入力画像の2乗を累算器に加算します．

パラメタ:	src – 1- または 3-チャンネル，8ビットまたは 32ビット浮動小数点型の入力画像 dst – 入力画像と同じチャンネル数，32ビットまたは 64ビット浮動小数点型の累算器画像 mask – オプションである処理マスク

関数 accumulateSquare は，入力画像 src またはその選択領域を2乗し，累算器 dst に加えます：

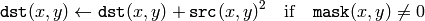
$\texttt{dst} (x,y) \leftarrow \texttt{dst} (x,y) + \texttt{src} (x,y)^2 \quad \text{if} \quad \texttt{mask} (x,y) \ne 0$

この関数は，マルチチャンネル画像をサポートしており，各チャンネルは個別に処理されます．

参考： accumulateSquare() , accumulateProduct() , accumulateWeighted()

cv::accumulateProduct¶

void accumulateProduct(const Mat& src1, const Mat& src2, Mat& dst, const Mat& mask=Mat())¶

2つの入力画像の要素毎の積を累算機に加える．

パラメタ:	src1 – 1- または 3-チャンネル，8ビットまたは 32ビット浮動小数点型の1番目の入力画像 src2 – `src1` と同じ型，同じサイズの2番目の入力画像 dst – 入力画像と同じチャンネル数の累算器画像．32ビットまたは 64ビット浮動小数点型 mask – オプションである処理マスク

関数 accumulateProduct は，2つの画像同士，またはその選択領域同士の積を累算器 dst に加えます：

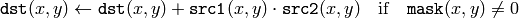
$\texttt{dst} (x,y) \leftarrow \texttt{dst} (x,y) + \texttt{src1} (x,y) \cdot \texttt{src2} (x,y) \quad \text{if} \quad \texttt{mask} (x,y) \ne 0$

この関数は，マルチチャンネル画像をサポートしており，各チャンネルは個別に処理されます．

参考： accumulate() , accumulateSquare() , accumulateWeighted()

cv::accumulateWeighted¶

void accumulateWeighted(const Mat& src, Mat& dst, double alpha, const Mat& mask=Mat())¶

移動平均値を更新します．

パラメタ:	src – 1- または 3-チャンネル，8ビットまたは 32ビット浮動小数点型の入力画像 dst – 入力画像と同じチャンネル数，32ビットまたは 64ビット浮動小数点型の累算器画像 alpha – 入力画像の重み mask – オプションである処理マスク

関数 accumulateWeightedg は， dst がフレーム列の移動平均になるように，入力画像 src と累積器 dst との重み付き和を求めます：

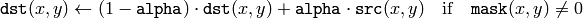
$\texttt{dst} (x,y) \leftarrow (1- \texttt{alpha} ) \cdot \texttt{dst} (x,y) + \texttt{alpha} \cdot \texttt{src} (x,y) \quad \text{if} \quad \texttt{mask} (x,y) \ne 0$

つまり， alpha は，更新速度（どのくらいの早さで，以前の画像を「忘れる」か）を調節します．この関数は，マルチチャンネル画像をサポートしており，各チャンネルは個別に処理されます．

参考： accumulate() , accumulateSquare() , accumulateProduct()

cv::calcOpticalFlowPyrLK¶

void calcOpticalFlowPyrLK(const Mat& prevImg, const Mat& nextImg, const vector<Point2f>& prevPts, vector<Point2f>& nextPts, vector<uchar>& status, vector<float>& err, Size winSize=Size(15, 15), int maxLevel=3, TermCriteria criteria=TermCriteria( TermCriteria::COUNT+TermCriteria::EPS, 30, 0.01), double derivLambda=0.5, int flags=0)¶

画像ピラミッドを利用してLucas-Kanade 法を反復実行することにより，疎な特徴集合に対するオプティカルフローを求めます．

パラメタ:

prevImg – 8ビット，シングルチャンネルまたは3-チャンネルの，1番目の入力画像
nextImg – prevImg と同じサイズ，同じ型の2番目の入力画像
prevPts – フローを検出する必要がある（特徴）点のベクトル
nextPts – 出力される（特徴）点のベクトル．2番目の入力画像における，特徴点の新たに計算された位置が格納されます
status – 出力状態ベクトル．特徴点のフローが検出された場合には，このベクトルの対応する要素が1に設定され，そうでない場合は0に設定されます
err – 移動前の特徴点の周辺領域と，移動後の特徴点の周辺領域との差を含む出力ベクトル
winSize – 各ピラミッドレベルにおける探索窓のサイズ
maxLevel – 画像ピラミッドの最大レベル数（0基準）．これが0の場合は，画像ピラミッドは利用されません（レベル1）．1の場合は，レベル2の画像ピラミッドが利用されます
criteria – 反復探索アルゴリズムの停止基準（指定された最大反復数 criteria.maxCount に達するか，探索窓が criteria.epsilon より小さい距離しか移動しなくなる状態）を指定します
derivLambda – オプティカルフローの推定に影響を与える，画像の空間微分の相対的な重み． derivLambda=0 ならば，画像の輝度値のみが利用され， derivLambda=1 ならば，画像の微分値のみが利用されます．0から1の間にある場合は，輝度値と微分値の両方が（それぞれ指定された比率で）利用されます
flags –
処理フラグ：
- OPTFLOW_USE_INITIAL_FLOW nextPts に格納されている初期推定値を利用します．このフラグがセットされない場合，最初に 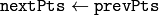$\texttt{nextPts}\leftarrow\texttt{prevPts}$ とされます

関数 calcOpticalFlowPyrLK は，Lucas-Kanade法を利用したオプティカルフローの疎な反復バージョンの実装です．詳しくは Bouguet00 を参照してください．

cv::calcOpticalFlowFarneback¶

void calcOpticalFlowFarneback(const Mat& prevImg, const Mat& nextImg, Mat& flow, double pyrScale, int levels, int winsize, int iterations, int polyN, double polySigma, int flags)¶

Gunnar Farneback のアルゴリズムを用いて，密なオプティカルフローを求めます．

パラメタ:

prevImg – 8ビット，シングルチャンネルの1番目の入力画像
nextImg – prevImg と同じサイズ，同じ型の2番目の入力画像
flow – 計算されたフロー画像．サイズは prevImg と同じで，型は CV_32FC2
pyrScale – それぞれの画像に対する画像ピラミッドを作るためのスケール (<1) を指定します． pyrScale=0.5 は，隣り合う各層において，各層が前の層の半分のサイズになっている古典的画像ピラミッドを意味します
levels – 最初の画像を含む，画像ピラミッドの層の数． levels=1 は，追加の層が作成されず，元画像だけが利用されることを意味します
winsize – 平均化窓サイズ．この値が大きくなると，画像のノイズに対するアルゴリズムの頑健さが増し，高速なモーションを検出できる場合が多くなります．しかし，ボケたモーションフィールドを生成することになります
iterations – 画像ピラミッドの各レベルにおける，アルゴリズムの反復数
polyN – 各ピクセルにおける多項式展開を求めるために利用される，ピクセル近傍領域のサイズ．この値が大きくなると，画像はより滑らかなサーフェイスで近似され，アルゴリズムの頑健さは増します，しかし同時に，ボケたモーションフィールドも増加します．一般的には， polyN =5 あるいは 7 となります
polySigma – 多項式展開の基底として利用される導関数を滑らかにするための，ガウス分布の標準偏差． polyN=5 ならば polySigma=1.1 ， polyN=7 ならば polySigma=1.5 が適当な値です
flags –
処理フラグ．以下の値の組み合わせ：
- OPTFLOW_USE_INITIAL_FLOW 入力 flow をフローの初期推定値として利用します
- OPTFLOW_FARNEBACK_GAUSSIAN オプティカルフロー推定のために，同サイズのボックスフィルタの代わりに 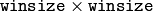$\texttt{winsize}\times\texttt{winsize}$ サイズのガウシアンフィルタを利用します．通常，このオプションによって処理速度は低下しますが，ボックスフィルタを利用する場合よりも正確なフローを求めることができます（また，同程度の頑健性を得るためには，ガウシアン窓の winsize をより大きくしなければいけません）

この関数は，以下を満たすようなアルゴリズムを利用して， prevImg の各ピクセルのオプティカルフローを求めます．

$\texttt{prevImg} (x,y) \sim \texttt{nextImg} ( \texttt{flow} (x,y)[0], \texttt{flow} (x,y)[1])$

cv::updateMotionHistory¶

void updateMotionHistory(const Mat& silhouette, Mat& mhi, double timestamp, double duration)¶

動作を表すシルエット画像を用いて，モーション履歴画像を更新します．

パラメタ:

silhouette – モーションが発生した場所が 0 以外のピクセル値をもつシルエットマスク
mhi – この関数によって更新される，モーション履歴画像（シングルチャンネル，32ビット浮動小数点型）
timestamp – ミリ秒単位，あるいは別の単位で表される現在時間
duration – timestamp と同じ単位で表される，モーションの最大持続時間

関数 updateMotionHistory は，モーション履歴画像を以下のように更新します：

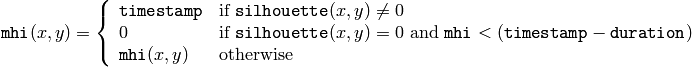
$\texttt{mhi} (x,y)= \forkthree{\texttt{timestamp}}{if $\texttt{silhouette}(x,y) \ne 0$}{0}{if $\texttt{silhouette}(x,y) = 0$ and $\texttt{mhi} < (\texttt{timestamp} - \texttt{duration})$}{\texttt{mhi}(x,y)}{otherwise}$

つまり，モーションが発生した場所の MHI（モーション履歴画像）ピクセルには，現在のタイムスタンプがセットされます．また，モーションが発生からある程度以上時間が経ったピクセルの値はクリアされます．

この関数は， calcMotionGradient() や calcGlobalOrientation() と共に，モーションテンプレートの実装となっています．このテクニックについては， Davis97 と Bradski00 で述べられています．

すべてのモーションテンプレート関数を実演する OpenCV のサンプル motempl.c を参照してください．

cv::calcMotionGradient¶

void calcMotionGradient(const Mat& mhi, Mat& mask, Mat& orientation, double delta1, double delta2, int apertureSize=3)¶

モーション履歴画像の勾配方向を求めます．

パラメタ:

mhi – シングルチャンネル，浮動小数点型のモーション履歴画像
mask – 型が CV_8UC1 で， mhi と同じサイズの出力マスク画像．この非0の要素が，その場所でのモーション勾配データが有効であることを示します
orientation – 出力されるモーション勾配方向画像． mhi と同じサイズ，同じ型．これの各ピクセル値は，0から360までの度単位で表されるモーション勾配方向となります
delta1, delta2 –
ピクセル近傍領域内の mhi の値がとるべき範囲を表す最小値と最大値．つまり，この関数はまず，各ピクセルの 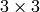$3 \times 3$ の近傍領域において，最小 ( 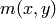$m(x,y)$ ) および最大 ( 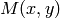$M(x,y)$ )の mhi を求めます．そして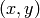， $(x, y)$ におけるモーション勾配方向が次の条件を満たす場合のみ有効であるとします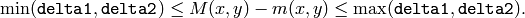

$\min ( \texttt{delta1} , \texttt{delta2} ) \le M(x,y)-m(x,y) \le \max ( \texttt{delta1} , \texttt{delta2} ).$
apertureSize – Sobel() のアパーチャサイズ

関数 calcMotionGradient は，各ピクセル 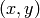$(x, y)$ における勾配方向を次のように求めます：

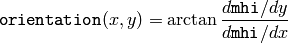
$\texttt{orientation} (x,y)= \arctan{\frac{d\texttt{mhi}/dy}{d\texttt{mhi}/dx}}$

（実際には，度単位で表現された計算角度が，全方位0から360までをカバーするように， fastArctan() と phase() が利用されます）．また， mask は，その場所で求められた角度が有効であることを示すピクセル値で埋められます．

cv::calcGlobalOrientation¶

double calcGlobalOrientation(const Mat& orientation, const Mat& mask, const Mat& mhi, double timestamp, double duration)¶

複数の選択領域の全体的なモーション方向を求めます．

パラメタ:

orientation – 関数 calcMotionGradient() によって求められた，モーション勾配方向画像
mask – マスク画像． calcMotionGradient() で求められた有効勾配のマスクと，方向を計算する必要がある領域を示すマスクの論理積
mhi – updateMotionHistory() によって求められた，モーション履歴画像
timestamp – updateMotionHistory() に渡されるタイムスタンプ
duration – ミリ秒単位で表される，モーションの最大持続時間． updateMotionHistory() に渡されます

関数 calcGlobalOrientation は，選択領域におけるモーションの平均方向を求め，その0から360までの角度を返します．平均方向は，重み付きの方向ヒストグラムから計算されます．これは mhi に記録されているように，最近のモーションが大きな重みを持ち，以前のモーションがより小さな重みを持ちます．

cv::CamShift¶

RotatedRect CamShift(const Mat& probImage, Rect& window, TermCriteria criteria)¶

物体の中心，サイズ，姿勢を求めます．

パラメタ:	probImage – 物体のヒストグラムのバックプロジェクション（ `calcBackProject()` を参照してください） window – 探索窓の初期状態 criteria – `meanShift()` 内部で利用される，停止基準

関数 CamShift は， Bradski98 で述べられている CAMSHIFT 物体追跡アルゴリズムの実装です．

まず， meanShift() を用いて物体の中心を求め，物体サイズに合わせて窓サイズを調整して，さらに最適な方向を検出します．この関数は，物体の位置，サイズ，姿勢を含む，回転した矩形を表現する構造体を返します．探索窓の次の位置は， RotatedRect::boundingRect() から得ることができます．

カラー物体を追跡する OpenCV サンプル camshiftdemo.c を参照してください．

cv::meanShift¶

int meanShift(const Mat& probImage, Rect& window, TermCriteria criteria)¶

バックプロジェクション画像上の物体中心を求める．

パラメタ:	probImage – 物体のヒストグラムのバックプロジェクション． `calcBackProject()` を参照してください window – 探索窓の初期状態 criteria – 反復探索アルゴリズムで利用される，停止基準

この関数は，物体の反復探索アルゴリズムの実装です．これは，物体のバックプロジェクションと初期位置を入力としてとります．バックプロジェクション画像の window 内の重心が計算され，探索窓の中心が，その重心に合うよう移動されます．この処理は，反復数が規定回数 criteria.maxCount に達するか，探索窓の移動距離が criteria.epsilon 以下になるまで繰り返されます．このアルゴリズムは， CamShift() 内部でも利用されていますが，これは CamShift() とは異なり，探索中に探索窓のサイズや姿勢は変化しません． calcBackProject() の出力を単純にこの関数に渡すことができますが，バックプロジェクションを事前にフィルタリングしてノイズを除去することで，より良い結果を得ることができます（例えば， findContours() を利用して連結成分を抽出， contourArea() を利用して小さい領域の輪郭を削除，そして残った輪郭を drawContours() によって描画します）．

KalmanFilter¶

KalmanFilter¶

カルマンフィルタクラス．

class KalmanFilter
{
public:
    KalmanFilter();newline
    KalmanFilter(int dynamParams, int measureParams, int controlParams=0);newline
    void init(int dynamParams, int measureParams, int controlParams=0);newline
    // statePost から statePre を予測します．
    const Mat& predict(const Mat& control=Mat());newline
    // 入力された観測ベクトルに基づき statePre を更新して，
    // その結果を statePost に格納します．
    const Mat& correct(const Mat& measurement);newline

    Mat statePre;           // 状態の推定値 (x'(k)):
                            //    x(k)=A*x(k-1)+B*u(k)
    Mat statePost;          // 更新された状態の推定値 (x(k)):
                            //    x(k)=x'(k)+K(k)*(z(k)-H*x'(k))
    Mat transitionMatrix;   // システムの時間遷移に関する線形モデル (A)
    Mat controlMatrix;      // 制御行列 (B)
                            //   （制御していない場合は，これは利用されません）
    Mat measurementMatrix;  // 観測行列 (H)
    Mat processNoiseCov;    // プロセスノイズ（時間遷移に関するノイズ）の共分散行列 (Q)
    Mat measurementNoiseCov;// 観測ノイズの共分散行列 (R)
    Mat errorCovPre;        // 今の時刻の誤差行列 (P'(k)):
                            //    P'(k)=A*P(k-1)*At + Q)*/
    Mat gain;               // 最適カルマンゲイン (K(k)):
                            //    K(k)=P'(k)*Ht*inv(H*P'(k)*Ht+R)
    Mat errorCovPost;       // 更新された誤差の共分散行列 (P(k)):
                            //    P(k)=(I-K(k)*H)*P'(k)
    ...
};

このクラスは，標準的なカルマンフィルタ http://en.wikipedia.org/wiki/Kalman_filter の実装です．しかし，ユーザは transitionMatrix , controlMatrix および measurementMatrix を変更して，拡張カルマンフィルタとして動作するようにもできます．OpenCVのサンプル kalman.c を参照してください．

モーション解析と物体追跡¶

cv::accumulate¶

cv::accumulateSquare¶

cv::accumulateProduct¶

cv::accumulateWeighted¶

cv::calcOpticalFlowPyrLK¶

cv::calcOpticalFlowFarneback¶

cv::updateMotionHistory¶

cv::calcMotionGradient¶

cv::calcGlobalOrientation¶

cv::CamShift¶

cv::meanShift¶

KalmanFilter¶

ヘルプとフィードバック

目次

前のトピックへ

次のトピックへ

このページ

ナビゲーション

モーション解析と物体追跡¶

cv::accumulate¶

cv::accumulateSquare¶

cv::accumulateProduct¶

cv::accumulateWeighted¶

cv::calcOpticalFlowPyrLK¶

cv::calcOpticalFlowFarneback¶

cv::updateMotionHistory¶

cv::calcMotionGradient¶

cv::calcGlobalOrientation¶

cv::CamShift¶

cv::meanShift¶

KalmanFilter¶

ヘルプとフィードバック

目次

前のトピックへ

次のトピックへ

このページ

クイック検索

ナビゲーション