CV リファレンス マニュアル
-
画像処理(Image Processing)
- 勾配,エッジ,コーナー(Gradients, Edges and Corners)
- サンプリング,補間,幾何変換(Sampling, Interpolation and Geometrical Transforms)
- モルフォロジー演算(Morphological Operations)
- フィルタと色変換(Filters and Color Conversion)
- ピラミッドとその応用(Pyramids and the Applications)
- 画像分割,領域結合,輪郭検出(Image Segmentation, Connected Components and Contour Retrieval)
- 画像と形状のモーメント(Image and Contour Moments)
- 特殊な画像変換(Special Image Transforms)
- ヒストグラム(Histograms)
- マッチング(Matching)
- 構造解析(Structural Analysis)
- 輪郭処理(Contour Processing)
- 計算幾何(Computational Geometry)
- 平面細分割(Planar Subdivisions)
- モーション解析と物体追跡(Motion Analysis and Object Tracking)
- パターン認識(Pattern Recognition)
- カメラキャリブレーションと3次元再構成(Camera Calibration and 3D Reconstruction)
- 参考文献
構造解析(Structural Analysis)
計算幾何(Computational Geometry)
MaxRect
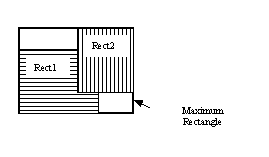
与えられた二つの矩形を包含する矩形を見つける
CvRect cvMaxRect( const CvRect* rect1, const CvRect* rect2 );
- rect1
- 一つ目の矩形.
- rect2
- 二つ目の矩形.
関数cvMaxRectは,入力した二つの長方形を含む最小の矩形領域を見つける.
CvBox2D
回転が考慮された2次元の箱
typedef struct CvBox2D
{
CvPoint2D32f center; /* 箱の中心 */
CvSize2D32f size; /* 箱の幅と長さ */
float angle; /* 水平軸と始めの辺(長さ方向の辺)との角度(度) */
}
CvBox2D;
PointSeqFromMat
点のベクトルを用いて,点のシーケンスヘッダを初期化する
CvSeq* cvPointSeqFromMat( int seq_kind, const CvArr* mat,
CvContour* contour_header,
CvSeqBlock* block );
- seq_kind
- 点のシーケンスの種類:点のセット(0),曲線(CV_SEQ_KIND_CURVE),閉曲線(CV_SEQ_KIND_CURVE+CV_SEQ_FLAG_CLOSED)等.
- mat
- 入力行列.点の連続的な1次元ベクトルで,CV_32SC2型かCV_32FC2型でなければならない.
- contour_header
- 輪郭ヘッダ.この関数で初期化される.
- block
- シーケンスブロックヘッダ.この関数で初期化される.
関数cvPointSeqFromMatは,指定した行列に含まれる要素をもつ「仮想的」なシーケンスを生成するために,シーケンスヘッダを初期化する. データはコピーされない.初期化されたシーケンスヘッダは,点のシーケンスを入力とする様々な関数に渡される. このシーケンスに新たな要素は追加されないが,幾つかは削除される可能性がある. この関数はcvMakeSeqHeaderForArray を内部的に利用しており,これの特別な形である. この関数は初期化された輪郭へのポインタを返す.包含矩形(構造体CvContourのrectはこの関数では初期化されない)を求めるには, cvBoundingRectを使うとよい.
簡単な使い方を以下に示す.
CvContour header; CvSeqBlock block; CvMat* vector = cvCreateMat( 1, 3, CV_32SC2 ); CV_MAT_ELEM( *vector, CvPoint, 0, 0 ) = cvPoint(100,100); CV_MAT_ELEM( *vector, CvPoint, 0, 1 ) = cvPoint(100,200); CV_MAT_ELEM( *vector, CvPoint, 0, 2 ) = cvPoint(200,100); IplImage* img = cvCreateImage( cvSize(300,300), 8, 3 ); cvZero(img); cvDrawContours( img, cvPointSeqFromMat(CV_SEQ_KIND_CURVE+CV_SEQ_FLAG_CLOSED, vector, &header, &block), CV_RGB(255,0,0), CV_RGB(255,0,0), 0, 3, 8, cvPoint(0,0));
BoxPoints
箱の頂点を見つける
void cvBoxPoints( CvBox2D box, CvPoint2D32f pt[4] );
- box
- 箱.
- pt
- 頂点の配列.
関数cvBoxPointsは入力した2次元の箱の頂点を計算する.この関数のコードを以下に示す.
void cvBoxPoints( CvBox2D box, CvPoint2D32f pt[4] )
{
double angle = box.angle*CV_PI/180.
float a = (float)cos(angle)*0.5f;
float b = (float)sin(angle)*0.5f;
pt[0].x = box.center.x - a*box.size.height - b*box.size.width;
pt[0].y = box.center.y + b*box.size.height - a*box.size.width;
pt[1].x = box.center.x + a*box.size.height - b*box.size.width;
pt[1].y = box.center.y - b*box.size.height - a*box.size.width;
pt[2].x = 2*box.center.x - pt[0].x;
pt[2].y = 2*box.center.y - pt[0].y;
pt[3].x = 2*box.center.x - pt[1].x;
pt[3].y = 2*box.center.y - pt[1].y;
}
FitEllipse
2次元の点列に楕円をフィッティングする
CvBox2D cvFitEllipse2( const CvArr* points );
- points
- 点のシーケンス,または配列.
関数cvFitEllipseは,(最小ニ乗推定によって)2次元の点列にフィットする最良の楕円を計算する. 返される構造体の意味は cvEllipseと似ているが,sizeには楕円の軸の半分の長さではなく, 全長が格納されている点が異なる.
FitLine
2次元または3次元の点列に線をフィッティングする
void cvFitLine( const CvArr* points, int dist_type, double param,
double reps, double aeps, float* line );
- points
- 32ビット整数型または浮動小数点型の2次元または3次元の点の配列,またはシーケンス.
- dist_type
- フィッティングに使われる距離(下の解説を参照).
- param
- それぞれの距離関数における数値パラメータ(C).0を指定した場合,最適な値が選択される.
- reps, aeps
- 半径(座標原点と線の距離)と角度に対する精度.それぞれ0.01が初期値として適している.
- line
- 出力される線のパラメータ.2次元フィッティングの場合,四つの浮動小数点型数(vx, vy, x0, y0)の配列で,(vx, vy)は正規化された方向ベクトル,(x0, y0)は線上の点を意味する.3次元フィッティングの場合,(vx, vy, vz, x0, y0, z0)の六つの浮動小数点型数の配列で,(vx, vy, vz)は正規化された方向ベクトル,(x0, y0, z0)は線上の点を意味する.
関数cvFitLineは,2次元または3次元の点列に対して sumiρ(ri)を最小化することで線をフィッティングする. ここでriはi番目の点と線の距離, ρ(r)は距離関数を示す.
dist_type=CV_DIST_L2 (L2):
ρ(r)=r2/2 (最も単純で高速な最小二乗法)
dist_type=CV_DIST_L1 (L1):
ρ(r)=r
dist_type=CV_DIST_L12 (L1-L2):
ρ(r)=2•[sqrt(1+r2/2) - 1]
dist_type=CV_DIST_FAIR (Fair):
ρ(r)=C2•[r/C - log(1 + r/C)], C=1.3998
dist_type=CV_DIST_WELSCH (Welsch):
ρ(r)=C2/2•[1 - exp(-(r/C)2)], C=2.9846
dist_type=CV_DIST_HUBER (Huber):
ρ(r)= r2/2, if r < C
C•(r-C/2), otherwise; C=1.345
ConvexHull2
点列の凸包を見つける
CvSeq* cvConvexHull2( const CvArr* input, void* hull_storage=NULL,
int orientation=CV_CLOCKWISE, int return_points=0 );
- points
- 32ビット整数型,もしくは浮動小数点型で表された2次元の点のシーケンスまたは配列.
- hull_storage
- 凸包を格納した出力配列(CvMat*),またはメモリストレージ (CvMemStorage*).配列の場合,1次元でなければならず,入力した配列/シーケンスと同じ要素数を持たなければならない.出力時にヘッダが変更されて,凸包のサイズまで配列が切り詰められる.
- orientation
- 凸包を構成するデータの並び.CV_CLOCKWISE,またはCV_COUNTER_CLOCKWISE.
- return_points
- このパラメータが0で,hull_storageが配列の場合にはインデックスが,メモリストレージの場合にはポインタが出力配列に格納される.0でない場合,凸包を表す点の集合自身が格納される.
関数cvConvexHull2は,Sklanskyのアルゴリズムを使って2次元の点列の凸包を見つける. hull_storageがメモリストレージの場合, この関数はreturn_pointsの値に応じて凸包の点, またはそれらへのポインタを含んだシーケンスを生成し,そのシーケンスを返す.
(例)点のシーケンスまたは配列の凸包を生成する
#include "cv.h"
#include "highgui.h"
#include <stdlib.h>
#define ARRAY 0 /* 0<=>1で配列かシーケンスを切り替える*/
void main( int argc, char** argv )
{
IplImage* img = cvCreateImage( cvSize( 500, 500 ), 8, 3 );
cvNamedWindow( "hull", 1 );
#if !ARRAY
CvMemStorage* storage = cvCreateMemStorage();
#endif
for(;;)
{
int i, count = rand()%100 + 1, hullcount;
CvPoint pt0;
#if !ARRAY
CvSeq* ptseq = cvCreateSeq( CV_SEQ_KIND_GENERIC|CV_32SC2, sizeof(CvContour),
sizeof(CvPoint), storage );
CvSeq* hull;
for( i = 0; i < count; i++ )
{
pt0.x = rand() % (img->width/2) + img->width/4;
pt0.y = rand() % (img->height/2) + img->height/4;
cvSeqPush( ptseq, &pt0 );
}
hull = cvConvexHull2( ptseq, 0, CV_CLOCKWISE, 0 );
hullcount = hull->total;
#else
CvPoint* points = (CvPoint*)malloc( count * sizeof(points[0]));
int* hull = (int*)malloc( count * sizeof(hull[0]));
CvMat point_mat = cvMat( 1, count, CV_32SC2, points );
CvMat hull_mat = cvMat( 1, count, CV_32SC1, hull );
for( i = 0; i < count; i++ )
{
pt0.x = rand() % (img->width/2) + img->width/4;
pt0.y = rand() % (img->height/2) + img->height/4;
points[i] = pt0;
}
cvConvexHull2( &point_mat, &hull_mat, CV_CLOCKWISE, 0 );
hullcount = hull_mat.cols;
#endif
cvZero( img );
for( i = 0; i < count; i++ )
{
#if !ARRAY
pt0 = *CV_GET_SEQ_ELEM( CvPoint, ptseq, i );
#else
pt0 = points[i];
#endif
cvCircle( img, pt0, 2, CV_RGB( 255, 0, 0 ), CV_FILLED );
}
#if !ARRAY
pt0 = **CV_GET_SEQ_ELEM( CvPoint*, hull, hullcount - 1 );
#else
pt0 = points[hull[hullcount-1]];
#endif
for( i = 0; i < hullcount; i++ )
{
#if !ARRAY
CvPoint pt = **CV_GET_SEQ_ELEM( CvPoint*, hull, i );
#else
CvPoint pt = points[hull[i]];
#endif
cvLine( img, pt0, pt, CV_RGB( 0, 255, 0 ));
pt0 = pt;
}
cvShowImage( "hull", img );
int key = cvWaitKey(0);
if( key == 27 ) // 'ESC'
break;
#if !ARRAY
cvClearMemStorage( storage );
#else
free( points );
free( hull );
#endif
}
}
CheckContourConvexity
輪郭が凸であるかを調べる
int cvCheckContourConvexity( const CvArr* contour );
- contour
- テストする輪郭(点列のシーケンスか配列).
関数cvCheckContourConvexityは,入力した輪郭が凸かどうかを調べる. 輪郭は自己交差しないような単純なものでなければならない.
CvConvexityDefect
輪郭の凸包の凹状欠損を表す構造体
typedef struct CvConvexityDefect
{
CvPoint* start; /* 輪郭の凹状欠損の始点 */
CvPoint* end; /* 輪郭の凹状欠損の終点s */
CvPoint* depth_point; /* 凹状欠損のうちで凸包から最も遠い点 */
float depth; /* 最も遠い点と凸包間の距離 */
} CvConvexityDefect;
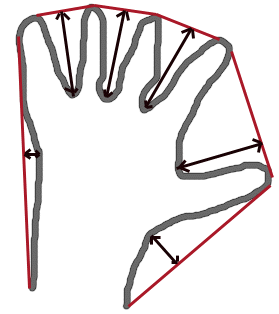
(図)手の輪郭の凹状欠損
ConvexityDefects
輪郭の凸包から凹状欠損を見つける
CvSeq* cvConvexityDefects( const CvArr* contour, const CvArr* convexhull,
CvMemStorage* storage=NULL );
- contour
- 入力輪郭.
- convexhull
- 凸包の点そのものではなく, 輪郭の点へのポインタまたはインデックスを持つ, つまりcvConvexHull2のreturn_pointsパラメータが0であるような cvConvexHull2 を使って得られた凸包.
- storage
- 凹状欠損の出力シーケンスを格納する変数.これがNULLである場合,代わりに,輪郭あるいは凸包のストレージが(この順番で)利用される.
関数cvConvexityDefectsは,入力輪郭の凸包の凹状欠損を全て見つけ,CvConvexityDefect構造体のシーケンスを返す.
PointPolygonTest
点と輪郭の関係を調べる
double cvPointPolygonTest( const CvArr* contour,
CvPoint2D32f pt, int measure_dist );
- contour
- 入力輪郭.
- pt
- 入力輪郭に対して調べる点.
- measure_dist
- 非0の場合,この関数は与えた点に最も近い輪郭までの距離を求める.
関数cvPointPolygonTestは,点が輪郭の内側にある か,外側にあるか,輪郭上に乗っている(あるいは,頂点と一致している)かを判別し,それぞれの場合に応じて正か負か0を返す. measure_dist=0の場合,戻り値はそれぞれ+1,-1,0である. measure_dist≠0の場合,点と最近傍輪郭までの符号付きの距離を返す.
この関数を使って,各ピクセルと輪郭との関係を調べた場合の出力結果の例を示す.

MinAreaRect2
与えられた2次元の点列を囲む最小矩形を求める
CvBox2D cvMinAreaRect2( const CvArr* points, CvMemStorage* storage=NULL );
- points
- 点のシーケンスまたは配列.
- storage
- 一時的なメモリストレージ.オプション.
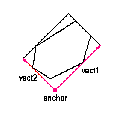
関数cvMinAreaRect2は,点列の凸包を求め,その凸包に対してrotating calipers法を適用することで,2次元の点列に対する最小矩形を見つける.
(図)輪郭を囲む最小矩形
MinEnclosingCircle
与えられた2次元の点列を囲む最小円を求める
int cvMinEnclosingCircle( const CvArr* points, CvPoint2D32f* center, float* radius );
- points
- 2次元の点のシーケンスまたは配列.
- center
- 出力パラメータ.囲む円の中心.
- radius
- 出力パラメータ.囲む円の半径.
関数cvMinEnclosingCircleは,反復法(iterative algorithm)を使って2次元の点列を囲む最小円を求める. 結果の円が全ての入力点を含む場合は非0を返し, それ以外(すなわちアルゴリズムの失敗)の場合は0を返す.
CalcPGH
輪郭の pair-wise geometrical histogram を求める
void cvCalcPGH( const CvSeq* contour, CvHistogram* hist );
- contour
- 入力輪郭.現在のところ座標が整数値の点のみが利用可能
- hist
- 求められたヒストグラム.必ず2次元になる.
関数cvCalcPGHは,与えられ輪郭に対して[Iivarinen97]に記述されている2次元のpair-wise geometrical histogram(PGH)を求める. このアルゴリズムでは輪郭エッジの全てのペアについて調査し,エッジ間の角度と最小/最大距離を求める. これを実行するために,この関数は全てのエッジをベースエッジとして順次取り込む.ベースエッジとそれ以外のエッジを調査し,非ベースエッジ上の点からの最小/最大距離とベースエッジとの角度を選び出す.エッジ間の角度がヒストグラムの横軸を表し,算出された最小/最大距離の差が縦軸として加算される(このヒストグラムは[Iivarninen97]の定義に対して相対的に転置されている). このヒストグラムは輪郭のマッチングに利用することができる.
