機械学習 リファレンス マニュアル
- イントロダクション,共通のクラスと関数(Introduction. Common classes and functions)
- ナイーブベイズ(単純ベイズ)分類器(Normal Bayes Classifier)
- K近傍法(K Nearest Neighbors)
- サポートベクターマシン(SVM)
- 決定木(Decision Trees)
- ブースティング(Boosting)
- ランダムツリー(Random Trees)
- EMアルゴリズム(Expectation-Maximization)
- ニューラルネットワーク(Neural Networks)
ニューラルネットワーク(Neural Networks)
MLでは,フィードフォワードのニューラルネットワークが用意されている. これは多層構造のパーセプトロン(MLP:multi-layer perceptrons)であり,最も一般的に使われるニューラルネットワークである. MLPは入力層と出力層,そして一つまたは複数の中間層から構成される. MLPのそれぞれの層は一つまたは複数のニューロンを含んでおり,前の層と次の層のニューロンが一方向に繋がれている. 下の図は3入力,2出力,中間層に5つのニューロンを持つ3層のパーセプトロンの例である.
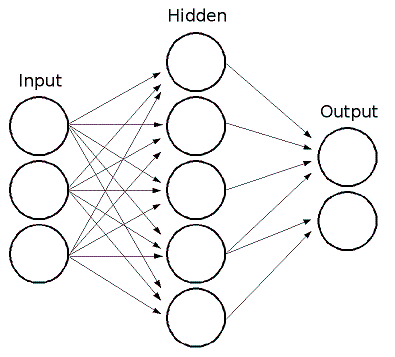
MLPの全てのニューロンは類似している. それらは幾つかの入力リンク(つまり前のレイヤーにある幾つかのニューロンからの出力値を入力として受け取る)と, 幾つかの出力リンク(つまり次のレイヤーの幾つかのニューロンに応答を渡す)を持つ. 前の層から受け取った値は,各ニューロン間のリンクで異なる幾らかの重みを掛けて足され,さらにバイアス項を足し合わされて, その合計値がニューロンによって異なる活性化関数fによって変換される. 以下に図を示す.
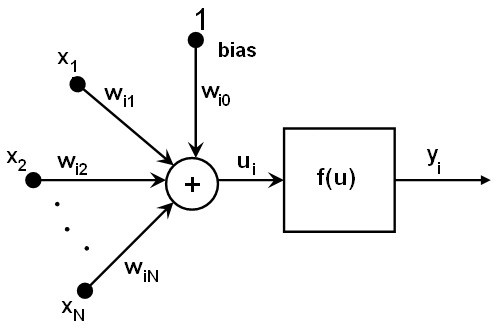
ui=sumj(w(n+1)i,j*xj) + w(n+1)i,bias
yi=f(ui)
異なった活性化関数が使われることもあり,MLでは標準的な3つの関数が実装されている.
- 恒等関数(CvANN_MLP::IDENTITY): f(x)=x
- 対称性を持つシグモイド関数(CvANN_MLP::SIGMOID_SYM):
f(x)=β*(1-e-αx)/(1+e-αx),
MLPにおけるデフォルトの選択.β=1, α=1を持つ標準シグモイド関数を以下に示す.
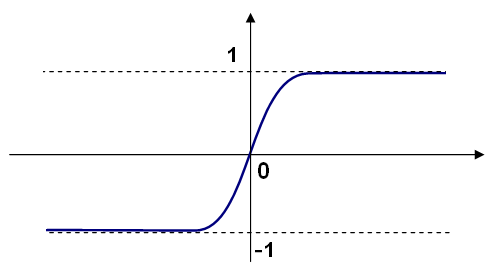
- ガウス関数(CvANN_MLP::GAUSSIAN): f(x)=βe-αx*x, 現時点では完全にはサポートされていない.
MLでは,すべてのニューロンは,ユーザが指定した同じフリーパラメータ(α,β)を持つ同じ活性化関数を使い,学習アルゴリズムによって変化しない.
そのため,学習済みのネットワークは全て次のように動作する. 入力として特徴ベクトルが必要で,そのベクトルのサイズは入力層のサイズと同じである. 値が最初の中間層に入力として渡されると,重みと活性化関数を使って中間層の出力が計算され,それが出力層に届くまで次々と下の層に流されてゆく.
従って,ネットワークを構築するためには,すべての重みw(n+1)i,jを知る必要がある. 重みは学習アルゴリズムによって計算される.このアルゴリズムは学習集合(複数の入力ベクトルとそれに対応する複数の出力ベクトル)を必要とし, 与えられた入力ベクトルに応じて期待通りの応答を出力するように,ネットワークの重みを繰り返し調節する.
ネットワークのサイズ(中間層の数とそれらのサイズ)が大きくなれば,ネットワークの柔軟性も増し,学習データセットでの誤差も小さくできるかもしれない. しかし同時に,この学習済みネットワークは学習データセットに存在するノイズ自体も「学習」してしまい,通常,ネットワークサイズがある程度の限界に達すると, テストセットの誤差も増加し始める. さらに,大きなネットワークでは小さいものと比較して学習に時間がかかるため,データの前処理 (PCAやそれに類似した手法を使う)を行い, 小さなネットワークに本質的な特徴のみを学習させる.
MLPの他の特徴として,カテゴリ変数データをそのままでは取り扱えないという問題があるが,これには回避策がある. 入力層,あるいは出力層(つまり,n>2に対するn-クラス分類器の場合)における特徴がカテゴリ変数であり, 異なるM個(>2)の値を扱うことができるとすると,その特徴がとりうるM個の値のうちi番目の値と等しい場合にのみ, i番目の要素が1となるようなM個要素の2値タプルとして表現できる.これは入力/出力層のサイズを増加させるが,学習アルゴリズムの収束を高速化し, 同時に「曖昧」な値,例えば固定値の代わりに確率の組を使うようなことを可能にする.
MLでは学習MLPのために二つのアルゴリズムが実装されている. 一つは古典的なランダムで逐次的な誤差逆伝播アルゴリズムであり, もう一つは,一括RPROPアルゴリズム(デフォルト)である.
参考文献
CvANN_MLP_TrainParams
MLP学習アルゴリズムのパラメータ
struct CvANN_MLP_TrainParams
{
CvANN_MLP_TrainParams();
CvANN_MLP_TrainParams( CvTermCriteria term_crit, int train_method,
double param1, double param2=0 );
~CvANN_MLP_TrainParams();
enum { BACKPROP=0, RPROP=1 };
CvTermCriteria term_crit;
int train_method;
// 誤差逆伝播のパラメータ
double bp_dw_scale, bp_moment_scale;
// rpropのパラメータ
double rp_dw0, rp_dw_plus, rp_dw_minus, rp_dw_min, rp_dw_max;
};
- term_crit
- 学習アルゴリズムの終了条件.アルゴリズムにより何度繰り返されるか (逐次型の誤差逆伝播アルゴリズムでは,この数は学習データセットのサイズと掛け合わされる)と,1ターンで重みをどの程度変更するかを指定する.
- train_method
- 用いる学習アルゴリズム. CvANN_MLP_TrainParams::BACKPROP(逐次型の誤差逆伝播アルゴリズム)または CvANN_MLP_TrainParams::RPROP(RPROPアルゴリズム,デフォルト値)のどちらか.
- bp_dw_scale
- (誤差逆伝播のみ):算出された重さの勾配に掛け合わされる係数.推奨される値は0.1程度である. このパラメータはコンストラクタのparam1で設定できる.
- bp_moment_scale
- (誤差逆伝播のみ):2つ前までのターンの重みの差を掛ける係数. このパラメータでは,重みのランダムな変動を滑らかにするための慣性を決定する. この値は0(無効にする)から1か,それ以上を取り得る.0.1程度が適当である. このパラメータはコンストラクタのparam2を通して設定できる.
- rp_dw0
- (RPROPのみ):重みdeltaの初期値.デフォルト値は0.1. このパラメータはコンストラクタのparam1を通して設定できる.
- rp_dw_plus
- (RPROPのみ):重みdeltaの増加係数.>1でなければならない. デフォルト値は1.2で,アルゴリズムの製作者によれば,多くの場合これで問題はない. このパラメータは構造体のメンバを修正して明示的に変えるしかない.
- rp_dw_minus
- (RPROPのみ):重みdeltaの減少係数. <1でなければならない.デフォルト値は0.5で,アルゴリズムの製作者によれば,多くの場合これで問題はない. このパラメータは構造体のメンバを修正して明示的に変えるしかない.
- rp_dw_min
- (RPROPのみ):重みdeltaの最小値.>0でなければならない. デフォルト値はFLT_EPSILON.このパラメータはコンストラクタのparam2を通して設定できる.
- rp_dw_max
- (RPROPのみ):重みdeltaの最大値.>1でなければならない. デフォルト値は50.このパラメータは構造体のメンバを修正して明示的に変えるしかない.
この構造体は,RPROPアルゴリズムのためのパラメータを初期化するデフォルトのコンストラクタを持つ. さらに高度なコンストラクタもあり,これはパラメータを自分なりに調整したり,誤差逆伝播アルゴリズムを選択することができる. 最終的に個々のパラメータは構造体が生成された後に調整される.
CvANN_MLP
MLPモデルクラス
class CvANN_MLP : public CvStatModel
{
public:
CvANN_MLP();
CvANN_MLP( const CvMat* _layer_sizes,
int _activ_func=SIGMOID_SYM,
double _f_param1=0, double _f_param2=0 );
virtual ~CvANN_MLP();
virtual void create( const CvMat* _layer_sizes,
int _activ_func=SIGMOID_SYM,
double _f_param1=0, double _f_param2=0 );
virtual int train( const CvMat* _inputs, const CvMat* _outputs,
const CvMat* _sample_weights, const CvMat* _sample_idx=0,
CvANN_MLP_TrainParams _params = CvANN_MLP_TrainParams(),
int flags=0 );
virtual float predict( const CvMat* _inputs,
CvMat* _outputs ) const;
virtual void clear();
// 利用可能な活性化関数
enum { IDENTITY = 0, SIGMOID_SYM = 1, GAUSSIAN = 2 };
// 利用可能な学習フラグ
enum { UPDATE_WEIGHTS = 1, NO_INPUT_SCALE = 2, NO_OUTPUT_SCALE = 4 };
virtual void read( CvFileStorage* fs, CvFileNode* node );
virtual void write( CvFileStorage* storage, const char* name );
int get_layer_count() { return layer_sizes ? layer_sizes->cols : 0; }
const CvMat* get_layer_sizes() { return layer_sizes; }
protected:
virtual bool prepare_to_train( const CvMat* _inputs, const CvMat* _outputs,
const CvMat* _sample_weights, const CvMat* _sample_idx,
CvANN_MLP_TrainParams _params,
CvVectors* _ivecs, CvVectors* _ovecs, double** _sw, int _flags );
// 逐次型のランダムな誤差逆伝播
virtual int train_backprop( CvVectors _ivecs, CvVectors _ovecs, const double* _sw );
// RPROPアルゴリズム
virtual int train_rprop( CvVectors _ivecs, CvVectors _ovecs, const double* _sw );
virtual void calc_activ_func( CvMat* xf, const double* bias ) const;
virtual void calc_activ_func_deriv( CvMat* xf, CvMat* deriv, const double* bias ) const;
virtual void set_activ_func( int _activ_func=SIGMOID_SYM,
double _f_param1=0, double _f_param2=0 );
virtual void init_weights();
virtual void scale_input( const CvMat* _src, CvMat* _dst ) const;
virtual void scale_output( const CvMat* _src, CvMat* _dst ) const;
virtual void calc_input_scale( const CvVectors* vecs, int flags );
virtual void calc_output_scale( const CvVectors* vecs, int flags );
virtual void write_params( CvFileStorage* fs );
virtual void read_params( CvFileStorage* fs, CvFileNode* node );
CvMat* layer_sizes;
CvMat* wbuf;
CvMat* sample_weights;
double** weights;
double f_param1, f_param2;
double min_val, max_val, min_val1, max_val1;
int activ_func;
int max_count, max_buf_sz;
CvANN_MLP_TrainParams params;
CvRNG rng;
};
ネットワーク構築と学習を一括して処理する他のMLのモデルとは異なり,MLPモデルでは,これらのステップは分離されている. まず,デフォルトではないコンストラクタかcreateメソッドを用いて,指定したトポロジーを持つネットワークを作成する. 全ての重みは0に設定される.そして,入出力ベクトルのセットを使ってネットワークを学習する. 学習処理は何度も繰り返される.すなわち重みは新しい学習データに基づいて調整される.
CvANN_MLP::create
指定したトポロジーでMLPを構築する
void CvANN_MLP::create(const CvMat* _layer_sizes,
int _activ_func=SIGMOID_SYM,
double _f_param1=0, double _f_param2=0 );
- _layer_sizes
- 入出力層を含む各層のニューロン数を指定する整数のベクトル.
- _activ_func
- 各ニューロンの活性化関数を指定する.次のうちのいずれか. CvANN_MLP::IDENTITY, CvANN_MLP::SIGMOID_SYM CvANN_MLP::GAUSSIAN.
- _f_param1, _f_param2
- 活性化関数のフリーパラメータαとβ.イントロダクションセクションの式を参照.
このメソッドは,指定したトポロジーのMLPネットワークを作成し,全てのニューロンに同じ活性化関数を与える.
CvANN_MLP::train
MLPの学習と更新
int CvANN_MLP::train(const CvMat* _inputs, const CvMat* _outputs,
const CvMat* _sample_weights, const CvMat* _sample_idx=0,
CvANN_MLP_TrainParams _params = CvANN_MLP_TrainParams(),
int flags=0 );
- _inputs
- 入力ベクトルの浮動小数点の行列で,1行で1ベクトル.
- _outputs
- 対応する出力ベクトルの浮動小数点の行列で,1行で1ベクトル.
- _sample_weights
- (RPROPのみ)各サンプルの重みを指定する浮動小数点のベクトル.オプション. 学習において,幾つかのサンプルは他のものより重要な場合がある. 例えば検出率と誤検出率間の適切なバランスを探すために,あるクラスの重みを増加させたい場合など.
- _sample_idx
- 用いるサンプルを表す整数のベクトル(すなわち_inputsと_outputsの行).
- _params
- 学習パラメータ.CvANN_MLP_TrainParamsを参照.
- _flags
- 学習アルゴリズムを制御する様々なパラメータ.以下を組み合わせて使う.
UPDATE_WEIGHTS = 1 - アルゴリズムはネットワークの重みを最初から計算せず,更新する (最初から計算する場合,重みはNguyen-Widrowアルゴリズムを使って初期化される).
NO_INPUT_SCALE - アルゴリズムは入力ベクトルを正規化しない.このフラグをセットしない場合, 学習アルゴリズムは平均値が0,標準偏差が1となるように,各入力を自主的に正規化する. 高頻度で更新されるネットワークの場合,新しい学習データは元のデータから大幅に異なる可能性がある. このような場合,ユーザは適切な正規化を導入する必要がある.
NO_OUTPUT_SCALE - アルゴリズムは出力ベクトルを正規化しない. このフラグをセットしない場合,学習アルゴリズムは使われた活性化関数に応じた範囲に納まるように,各出力を自主的に正規化する.
このメソッドは,指定した学習アルゴリズムを用いてネットワークの重みを計算/調整し,繰り返した回数を返す.
