CV リファレンス マニュアル
-
画像処理(Image Processing)
- 勾配,エッジ,コーナー,特徴(Gradients, Edges, Corners and Features)
- サンプリング,補間,幾何変換(Sampling, Interpolation and Geometrical Transforms)
- モルフォロジー演算(Morphological Operations)
- フィルタと色変換(Filters and Color Conversion)
- ピラミッドとその応用(Pyramids and the Applications)
- 画像分割,領域結合,輪郭検出(Image Segmentation, Connected Components and Contour Retrieval)
- 画像と形状のモーメント(Image and Contour Moments)
- 特殊な画像変換(Special Image Transforms)
- ヒストグラム(Histograms)
- マッチング(Matching)
- 構造解析(Structural Analysis)
- 輪郭処理(Contour Processing)
- 計算幾何(Computational Geometry)
- 平面細分割(Planar Subdivisions)
- モーション解析と物体追跡(Motion Analysis and Object Tracking)
- パターン認識(Pattern Recognition)
- カメラキャリブレーションと3次元再構成(Camera Calibration and 3D Reconstruction)
- 参考文献
構造解析(Structural Analysis)
平面細分割(Planar Subdivisions)
CvSubdiv2D
平面細分割のための構造体
#define CV_SUBDIV2D_FIELDS() \
CV_GRAPH_FIELDS() \
int quad_edges; \
int is_geometry_valid; \
CvSubdiv2DEdge recent_edge; \
CvPoint2D32f topleft; \
CvPoint2D32f bottomright;
typedef struct CvSubdiv2D
{
CV_SUBDIV2D_FIELDS()
}
CvSubdiv2D;
平面細分割とは,重複しない小領域(細分割面)で全平面を細分化することである. 上記の構造体は2次元の点集合によって細分割を表現し,各集合の点群は互いに連結され,平面グラフを構成する.この平面グラフは,無限領域での最も外側にある細分割点(凸包の頂点(群)と呼ばれる)に接続した少数のエッジを持ち,そのエッジによって平面を小平面に細分割する.
全ての細分割には,その面と点(細分割の頂点)の役割を入れ替えた双対細分割が存在する.すなわち双対細分割においては,面は頂点(以下,仮想点と呼ぶ)として,元の細分割の頂点は面として扱われる.下の図では,元の細分割が実線で,双対細分割が点線で示されている.
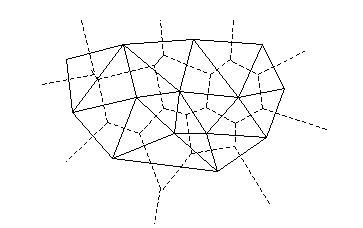
OpenCVでは,ドロネー(Delaunay)のアルゴリズムを使って平面を三角形に細分化する. 細分割は,確実に全ての細分点を含む仮想の三角形から開始し,反復計算により行われる. この場合,双対細分割は,入力された二次元の点群のボロノイ図となる. 細分割は平面の三次元区分変換や,モーフィング,平面上の点の高速配置,特別なグラフ(NNGやRNGなど)の生成などに用いられる.
CvQuadEdge2D
平面細分割のQuad-edge構造体
/* 4辺の内の一つ.下位2ビットはインデックス(0...3)で
上位ビットは4辺へのポインタ. */
typedef long CvSubdiv2DEdge;
/* quad-edge構造体フィールド */
#define CV_QUADEDGE2D_FIELDS() \
int flags; \
struct CvSubdiv2DPoint* pt[4]; \
CvSubdiv2DEdge next[4];
typedef struct CvQuadEdge2D
{
CV_QUADEDGE2D_FIELDS()
}
CvQuadEdge2D;
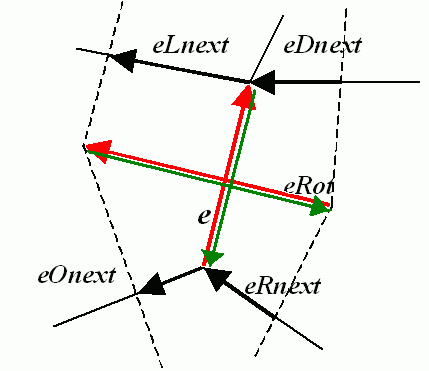
Quad-edgeは平面細分割の基本要素であり,4つの辺を持つ(e,eRot(赤)と eの反転,eRotの反転(緑)).
CvSubdiv2DPoint
オリジナルの細分割と双対細分割の点を表す構造体
#define CV_SUBDIV2D_POINT_FIELDS()\
int flags; \
CvSubdiv2DEdge first; \
CvPoint2D32f pt;
#define CV_SUBDIV2D_VIRTUAL_POINT_FLAG (1 << 30)
typedef struct CvSubdiv2DPoint
{
CV_SUBDIV2D_POINT_FIELDS()
}
CvSubdiv2DPoint;
Subdiv2DGetEdge
与えられた辺に関連する辺の一つを返す
CvSubdiv2DEdge cvSubdiv2DGetEdge( CvSubdiv2DEdge edge, CvNextEdgeType type );
#define cvSubdiv2DNextEdge( edge ) cvSubdiv2DGetEdge( edge, CV_NEXT_AROUND_ORG )
- edge
- 細分割平面の辺の一つ(quad-edge表現ではない).
- type
- 戻り値とする辺の条件を指定.以下のいずれか一つ:
- CV_NEXT_AROUND_ORG - 入力された辺の始点の近傍にある次の辺(eが入力のとき,上図のeOnext)
- CV_NEXT_AROUND_DST - 入力された辺の終点の近傍にある次の辺(eDnext)
- CV_PREV_AROUND_ORG - 入力された辺の始点の近傍にある一つ前の辺(eRnext の反転)
- CV_PREV_AROUND_DST - 入力された辺の終点の近傍にある一つ前の辺(eLnext の反転)
- CV_NEXT_AROUND_LEFT - 入力された辺を含む左面の次の辺 (eLnext)
- CV_NEXT_AROUND_RIGHT - 入力された辺を含む右面の次の辺(eRnext)
- CV_PREV_AROUND_LEFT - 入力された辺を含む左面の一つ前の辺(eOnext の反転)
- CV_PREV_AROUND_RIGHT - 入力された辺を含む右面の一つ前の辺(eDnext の反転)
関数 cvSubdiv2DGetEdge は,入力された辺に関連する辺の一つを返す.
Subdiv2DRotateEdge
同一のquad-edge内にある他の辺を返す
CvSubdiv2DEdge cvSubdiv2DRotateEdge( CvSubdiv2DEdge edge, int rotate );
- edge
- 細分割の辺(quad-edge表現ではない).
- type
- 関係の指定(入力された辺と同じquad-edgeのどの辺を返すかを指定).以下のいずれか一つ:
- 0 - 入力の辺(eが入力された場合, 上図の e 自身)
- 1 - 回転された辺(eRot)
- 2 - 反転された辺(eの反転(緑で表示))
- 3 - 反転と回転された辺(eRotの反転(緑で表示))
関数 cvSubdiv2DRotateEdge は,入力された辺を含むquad-edge中の辺の一つを返す.
Subdiv2DEdgeOrg
辺の始点を返す
CvSubdiv2DPoint* cvSubdiv2DEdgeOrg( CvSubdiv2DEdge edge );
- edge
- 細分割の辺(quad-edge表現ではない).
関数 cvSubdiv2DEdgeOrg は,辺の始点を返す. 辺が双対細分割のものであり,仮想点の座標がまだ計算されていない場合は,NULLポインタを返す. 仮想点は関数 cvCalcSubdivVoronoi2D を用いて計算される.
Subdiv2DEdgeDst
辺の終点を返す
CvSubdiv2DPoint* cvSubdiv2DEdgeDst( CvSubdiv2DEdge edge );
- edge
- 細分割の辺(quad-edge表現ではない).
関数 cvSubdiv2DEdgeDst は,辺の終点を返す. 辺が双対細分割のものであり,仮想点の座標がまだ計算されていない場合は,NULLポインタを返す. 仮想点は関数 cvCalcSubdivVoronoi2D を用いて計算される.
CreateSubdivDelaunay2D
空のドロネー三角形を作成する
CvSubdiv2D* cvCreateSubdivDelaunay2D( CvRect rect, CvMemStorage* storage );
- rect
- 細分割のために追加される全ての2次元点を包含する矩形.
- storage
- 細分割のための領域.
関数 cvCreateSubdivDelaunay2D は空のドロネー細分割構造体を作成する. 関数 cvSubdivDelaunay2DInsert を用いて,さらに2次元点を追加することが可能である. 追加される全ての点は指定された矩形領域内にある必要があり,領域外にある場合はランタイムエラーが発生する.
SubdivDelaunay2DInsert
ドロネー三角形に点を追加する
CvSubdiv2DPoint* cvSubdivDelaunay2DInsert( CvSubdiv2D* subdiv, CvPoint2D32f pt);
- subdiv
- 関数cvCreateSubdivDelaunay2D で作成されたドロネー細分割.
- pt
- 追加する点.
関数 cvSubdivDelaunay2DInsert は,細分割のために一つの点を追加し,細分割のトポロジー を適切に修正する. 同じ座標に点が既に存在している場合は,点の新規追加は行わない.この関数は,追加した点へのポインタを返す. この段階では,仮想点座標の計算は行われない.
Subdiv2DLocate
ドロネー三角形の点の位置を返す
CvSubdiv2DPointLocation cvSubdiv2DLocate( CvSubdiv2D* subdiv, CvPoint2D32f pt,
CvSubdiv2DEdge* edge,
CvSubdiv2DPoint** vertex=NULL );
- subdiv
- ドロネー,またはその他の細分割.
- pt
- 位置を知りたい点.
- edge
- 出力される辺.配置した点は,その辺上または右に存在する.
- vertex
- オプション出力.入力点と一致する細分割の頂点へのポインタのポインタ.
関数 cvSubdiv2DLocate は,入力された点を細分割の中に配置する. 5種類の場合がある.
- 点は小平面内に存在する.この関数は CV_PTLOC_INSIDE を返し,*edge はその面の辺の一つを含む.
- 点は辺上に存在する.この関数は CV_PTLOC_ON_EDGE を返し,*edge は該当する辺を含む.
- 点は細分割平面内の頂点と一致する.この関数は CV_PTLOC_VERTEX を返し,*vertex は該当する頂点のポインタを含む.
- 点は細分割平面の参照矩形の外にある.この関数は CV_PTLOC_OUTSIDE_RECT を返し,ポインタに何も値を入れない.
- 入力の引数が正しくないとき,ランタイムエラーが起こる.エラー処理モードが"silent" か "parent" の場合は, CV_PTLOC_ERROR が返される.
FindNearestPoint2D
与えられた点に最も近い細分割の頂点を求める
CvSubdiv2DPoint* cvFindNearestPoint2D( CvSubdiv2D* subdiv, CvPoint2D32f pt );
- subdiv
- ドロネー,または他の細分割.
- pt
- 入力点.
関数 cvFindNearestPoint2D は,入力点の細分割内での位置を求めるもう一つの関数である. この関数は入力された点に最も近い頂点を求める. cvSubdiv2DLocate を用いて求められた小平面が探索の開始点として用いられるが,これを構成する頂点の一つが入力点を含む必要はない. この関数は求められた細分割の頂点へのポインタを返す.
CalcSubdivVoronoi2D
ボロノイ図のセルの座標を計算する
void cvCalcSubdivVoronoi2D( CvSubdiv2D* subdiv );
- subdiv
- ドロネー細分割.全ての点は追加済みである.
関数 cvCalcSubdivVoronoi2D は,仮想点の座標を計算する.元の細分割面のある頂点に対応する仮想点全てを接続すると,その頂点を含むボロノイ領域の境界を構成する.
ClearSubdivVoronoi2D
全ての仮想点の削除する
void cvClearSubdivVoronoi2D( CvSubdiv2D* subdiv );
- subdiv
- ドロネー細分割.
関数 cvClearSubdivVoronoi2D は,全ての仮想点を削除する. この関数の前回の呼出し後に細分割が変更された場合,この関数は cvCalcSubdivVoronoi2D の内部で呼ばれる.
これらの関数の他に,平面細分割に用いられる低レベルの関数がいくつか存在する.cv.hやソースファイルを参照のこと. ランダムな2次元の点集合を用いて,ドロネー三角形分割やボロノイ図を作成するためのサンプルプログラムは, opencv/samples/c において参照できる.
