機械学習リファレンスマニュアル

最終変更者: 怡土順一, 最終変更リビジョン: 467, 最終変更日時: 2009-06-23 14:23:34 +0900 (火, 23 6月 2009)

EMアルゴリズム（Expectation-Maximization）

EM（Expectation-Maximization）アルゴリズムは，混合数が指定された混合ガウス分布に基づき，多変量の確率密度関数のパラメータを推定する．

特徴ベクトル{x₁, x₂,...,x_N} の集合を考える． d次元ユークリッド空間のN個のベクトルは，混合ガウス分布を用いて以下のように表現される．

ここでmは混合数，p_k は，平均a_k，共分散行列S_k， k-th分布の重みπ_kを持つ正規分布密度である．混合数mとサンプル{x_i, i=1..N}を与えることで，アルゴリズムはすべての混合分布パラメータ（すなわち， a_k，S_k，π_k）の最尤推定値（MLE）を以下のように推定する．

EMアルゴリズムは繰り返し処理を行う．各繰り返し処理には二つのステップを含む. 第1ステップ（Expectation-step，または E-step）では，混合分布#kに属するサンプル#iの確率 p_i,k（以下の式では α_i,k で表される）を，その時点の混合分布パラメータの推定値を用いて以下のように求める．

第2ステップ（Maximization-step，またはM-step）では以下のように，混合分布パラメータ推定値が，計算された確率を用いて高精度化される．

p_i,k の初期値が与えられる場合，アルゴリズムはM-stepから始めてもよい．また，p_i,kがわからない場合は，入力サンプルをあらかじめクラスタリングし，p_i,kの初期値を求めるために，シンプルなクラスタリングアルゴリズムを使用する．このような場合（MLも含む）， k-meansアルゴリズムがよく用いられる．

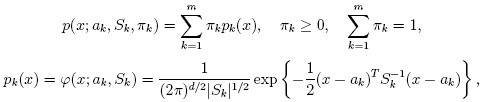
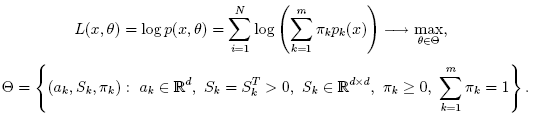
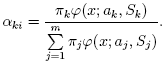
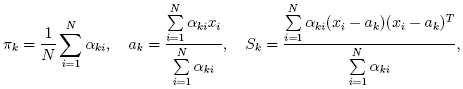
EMアルゴリズムが扱うべき問題の一つが，膨大な推定パラメータの数である．パラメータの大多数は共変動行列で表されており，それぞれd×dの要素（ここで，dは特徴空間の次元数である）を持つ．しかし，実際は，共変動行列のほとんどが対角行列であり，さらにμ_k*I （Iは単位行列，μ_k は混合分布に依存する「スケール」パラメータ）に非常に近い．従って，ロバストな計算を行うために，共変動行列により強い制約条件を付けた状態で計算を開始し，そこで推定されたパラメータを入力として，弱い制約条件下での最適化問題を解く（対角共変動行列は，既に十分な精度の近似値になっていることが多い）．

参考文献

[Bilmes98] J. A. Bilmes. A Gentle Tutorial of the EM Algorithm and its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models. Technical Report TR-97-021, International Computer Science Institute and Computer Science Division, University of California at Berkeley, April 1998.

CvEMParams

EMアルゴリズムのパラメータ

struct CvEMParams
{
    CvEMParams() : nclusters(10), cov_mat_type(CvEM::COV_MAT_DIAGONAL),
        start_step(CvEM::START_AUTO_STEP), probs(0), weights(0), means(0), covs(0)
    {
        term_crit=cvTermCriteria( CV_TERMCRIT_ITER+CV_TERMCRIT_EPS, 100, FLT_EPSILON );
    }

    CvEMParams( int _nclusters, int _cov_mat_type=1/*CvEM::COV_MAT_DIAGONAL*/,
                int _start_step=0/*CvEM::START_AUTO_STEP*/,
                CvTermCriteria _term_crit=cvTermCriteria(CV_TERMCRIT_ITER+CV_TERMCRIT_EPS, 
                                                         100, FLT_EPSILON),
                CvMat* _probs=0, CvMat* _weights=0, CvMat* _means=0, CvMat** _covs=0 ) :
                nclusters(_nclusters), cov_mat_type(_cov_mat_type), start_step(_start_step),
                probs(_probs), weights(_weights), means(_means), covs(_covs), term_crit(_term_crit)
    {}

    int nclusters;
    int cov_mat_type;
    int start_step;
    const CvMat* probs;
    const CvMat* weights;
    const CvMat* means;
    const CvMat** covs;
    CvTermCriteria term_crit;
};

nclusters: 混合数. EMアルゴリズムの実装のいくつかは，指定された値の範囲から，最適な混合数を決定することができる．しかし，MLの場合は，まだそのような事はできない．
cov_mat_type: 混合分布共変動行列のタイプ．次のうちの一つ．
CvEM::COV_MAT_GENERIC - それぞれの混合分布の共変動行列は任意の正定値対称行列であり，それぞれの行列における自由なパラメータ数は約d²/2である．かなり正確なパラメータの推定初期値があるか，学習サンプル数が膨大でない限り，このオプションを使用することは推奨されない．
CvEM::COV_MAT_DIAGONAL - それぞれの行列の共変動行列は任意の正の対角要素を持つ対角行列であり，対角以外の要素は0となる．そのため，自由なパラメータの数は，それぞれの行列でdである．これは良い推定結果をもたらすオプションとして一般的に最も使用される．
CvEM::COV_MAT_SPHERICAL - それぞれの行列の共変動行列は，スケーリングされた単位行列μ_k*Iである．そのため推定されるパラメータはμ_kのみである．このオプションは制約条件が関連する特別なケースや，最適化の第1ステップとして（例えば，データがPCA によって事前処理されている場合など）用いられることがある．このような予備推定の結果は，さらにcov_mat_type=CvEM::COV_MAT_DIAGONALを指定した最適化処理に渡される．
start_step: アルゴリズムをスタートする最初のステップ．次のうちの一つ．
CvEM::START_E_STEP - アルゴリズムはE-stepでスタートする. 少なくとも平均ベクトルの初期値 CvEMParams::means が渡されなければならない．オプションとして，ユーザは重み（CvEMParams::weights）と/または共変動行列（CvEMParams::covs）を与えることもできる．
CvEM::START_M_STEP - アルゴリズムはM-stepでスタートする.初期確率 p_i,k が与えられなければならない．
CvEM::START_AUTO_STEP - ユーザから必要な値が指定されない場合，k-meansアルゴリズムが混合分布パラメータの初期値推定に用いられる．
term_crit: 処理の終了条件．EMアルゴリズムは，特定の繰り返し回数（term_crit.num_iter）に達するか，繰り返し間における推定パラメータの変化が非常に小さくなった（term_crit.epsilonより小さい）場合に終了する．
probs: 確率p_i,kの初期値． start_step=CvEM::START_M_STEPのときのみ使用する（その場合はNULLであってはならない）．
weights: 混合分布の重みπ_kの初期値． start_step=CvEM::START_E_STEPのときのみ（NULLでない場合は）使用する.
covs: 混合分布の共変動行列S_kの初期値． start_step=CvEM::START_E_STEPのときのみ（NULLでない場合は）使用する．
means: 混合分布の平均 a_kの初期値． start_step=CvEM::START_E_STEPのときのみ使用する（その場合はNULLであってはならない）．

この構造体は二つのコンストラクタを持つ．デフォルトコンストラクタは，大まかな経験則に相当し（パラメータとしてデフォルト値を用いる），もう一つのコンストラクタは，一つの混合数（問題に依存する不可欠なパラメータ）から，混合パラメータの初期値まで，パラメータ数とその値を変更することが可能である．

CvEM

EMモデルクラス

class CV_EXPORTS CvEM : public CvStatModel
{
public:
    // 共変動行列のタイプ
    enum { COV_MAT_SPHERICAL=0, COV_MAT_DIAGONAL=1, COV_MAT_GENERIC=2 };

    // 初期ステップ
    enum { START_E_STEP=1, START_M_STEP=2, START_AUTO_STEP=0 };

    CvEM();
    CvEM( const CvMat* samples, const CvMat* sample_idx=0,
          CvEMParams params=CvEMParams(), CvMat* labels=0 );
    virtual ~CvEM();

    virtual bool train( const CvMat* samples, const CvMat* sample_idx=0,
                        CvEMParams params=CvEMParams(), CvMat* labels=0 );

    virtual float predict( const CvMat* sample, CvMat* probs ) const;
    virtual void clear();

    int get_nclusters() const { return params.nclusters; }
    const CvMat* get_means() const { return means; }
    const CvMat** get_covs() const { return covs; }
    const CvMat* get_weights() const { return weights; }
    const CvMat* get_probs() const { return probs; }

protected:

    virtual void set_params( const CvEMParams& params,
                             const CvVectors& train_data );
    virtual void init_em( const CvVectors& train_data );
    virtual double run_em( const CvVectors& train_data );
    virtual void init_auto( const CvVectors& samples );
    virtual void kmeans( const CvVectors& train_data, int nclusters,
                         CvMat* labels, CvTermCriteria criteria,
                         const CvMat* means );
    CvEMParams params;
    double log_likelihood;

    CvMat* means;
    CvMat** covs;
    CvMat* weights;
    CvMat* probs;

    CvMat* log_weight_div_det;
    CvMat* inv_eigen_values;
    CvMat** cov_rotate_mats;
};

CvEM::train

サンプル集合からガウス混合パラメータを推定する

void CvEM::train(const CvMat* samples, const CvMat*  sample_idx=0,
                  CvEMParams params=CvEMParams(), CvMat* labels=0 );

多くの機械学習のモデルとは異なり，EMアルゴリズムは教師なし学習アルゴリズムで，入力に対してクラスラベルや関数値を返さない．その代わりに，入力サンプル集合から，ガウス混合パラメータのMLE（最尤推定値）を計算し，構造体の中にすべてのパラメータを保存する（確率p_i,k，平均a_k，共変動S_k [k]，重みπ_k）．そしてオプションとして，それぞれのサンプルに出力として次のような「クラスラベル」を計算する（labels_i=arg max_k(p_i,k), i=1..N）．これはつまり，それぞれのサンプルについて可能性の高い混合分布のインデックスである.

学習後のモデルは，他のクラスタリング手法と同様に，予測に使用することができる．この学習済みモデルは normal bayes classifier に類似している．

（例）複数のガウス分布からランダムにサンプリングされたデータをEMを用いたクラスタリング